
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 6. Встроенные в систему цвм. Математические модели цифровых системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Преимущества и недостатки использования ЦВМ в контуре управления.
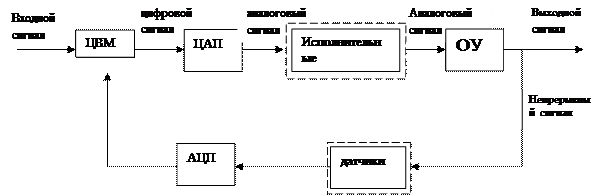
Достижению высокого качества управления способствует использование компьютера в контуре управления как основного звена системы управления,обрабатывающего информацию с датчиков и вырабатывающего команды на исполнительные органы. Встроенные в системы компьютеры, управляющие физическими процессами функционирования, решают задачи, отличные от задач «классической компьютерной обработки» информации. Основное отличие состоит в том, что управляющий компьютер должен работать со скоростью, соответствующей скорости управляемого процесса, динамика которого может быть весьма быстрой. Другая особенность компьютерных технологий управления процессами заключается в том, что часто ход исполнения ПО встроенной ЦВМ нельзя определить заранее из за необходимости реагировать на внешние события. Внешние сигналы могут прерывать и изменять последовательность исполнения программ ПО. Третья особенность связана с необходимостью обеспечения надежности и безопасности управления. Поэтому функции аварийной защиты обязательно поддерживаются ПО таких компьютеров. Работа ПО встроенных систем совместно с их оборудованием осложняется тем, что подчас возникшую ошибочную ситуацию трудно воспроизвести даже при отладке, поскольку каждый запуск системы сопровождается разными временными задержками, а от них зависит последовательность работы программных процессов, наложения прерываний на различные участки процессов и т.п. В рассматриваемых сложных системах управления с обратной связью функции управляющего устройства выполняет ЦВМ. Использование ЦВМ сулит большие преимущества в использовании сложных и эффективных алгоритмов управления. Однако за эти преимущества приходится платить некоторыми неблагоприятными эффектами. Главные преимущества ЦВМ в контуре управления СТС следующие: -имеется возможность реализации сложных законов управления, обеспечивающих высокую эффективность управления и достижения сложных целей управления, проведения алгоритмического контроля, -ЦВМ или сети ЦВМ являются системообразующим элементом системы и не только с концептуальной точки зрения, но и являются аппаратным ядром системы, определяя унифицированные электромеханические интерфейсы с аппаратурой системы, доступ к среде передачи информации и т.п. - цифровые устройства не дают разбросов выхода от температуры,качания напряжения,в отличие от аналоговых устройств, -простота модернизации системы путем модернизации ПО ЦВМ для перестройки законов управления. Поскольку ввод информации в компьютер, а так же вывод информации из него может принципиально осуществляться только в дискретные моменты времени, а не непрерывно (ЦВМ – дискретное устройство), то необходимо разработать также специальный метод математического описания и анализа качества работы цифровых систем управления. Негативная сторона цифрового управления связана с двумя эффектами: квантование по уровню и квантование по времени
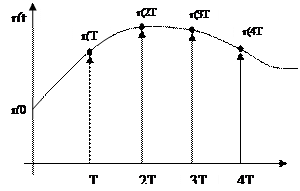
Рассмотрим мехатронную цифровую систему управления с обратной связью, в которой функции управляющего устройства выполняет ЦВМ. Цифровая система оперирует данными, получаемыми из непрерывного сигнала непрерывных физических устройств в равноотстоящие моменты времени, как правило, через устройство, называемое аналогово-цифровой преобразователь (АЦП). В результате получается временная последовательность данных, называемых квантованными по времени и уровню сигналами или дискретным сигналом. Аналоговые (непрерывные) устройства – исполнительные органы не воспринимают результаты, полученные в ЦВМ в виде потока бит. Поэтому результаты решения задач управления в ЦВМ преобразуются в аналоговую форму цифро-аналоговым преобразователем(ЦАП). Интервал дискретизации обрабатываемых данных и эффект транспонирования частот Цифровая система оперирует данными, получаемыми из непрерывного сигнала непрерывных физических устройств в равноотстоящие моменты времени, как правило, через устройство, называемое аналогово-цифровой преобразователь (АЦП). В результате получается временная последовательность данных, называемых квантованными по времени и уровню сигналами или дискретным сигналом. Аналоговые (непрерывные) устройства – исполнительные органы не воспринимают результаты, полученные в ЦВМ в виде потока бит. Поэтому результаты решения задач управления в ЦВМ преобразуются в аналоговую форму цифро-аналоговым преобразователем(ЦАП). Интервал дискретизации h должен быть достаточно мал, чтобы выходной сигнал с приемлемой точностью описывал изменения непрерывного входа. Поскольку после съема (выборки) и введения значения обрабатываемой переменной в ЦВМ о дальнейших их значениях ничего не известно до следующей выборки, период дискретизации должен быть настолько коротким, чтобы значение обрабатываемой перемененной не успело значительно измениться. Другими словами частота выборки должна быть достаточной для последующего восстановления непрерывного значения из дискретного. Нижний предел частоты выборки связан с динамикой процесса т.е. насколько быстро изменяются физические значения обрабатываемой переменной во времени. Теоретически частота дискретизации должна более чем в два раза превышать частоту наибольшей периодической составляющей рассматриваемого сигнала. В этом случае возможно восстановление хотя бы периода изменения переменной. Выбор интервала дискретизации проиллюстрирован ниже на примере. Для простоты рассмотрен чисто синусоидальный сигнал (переменная), помятуя, что каждый сигнал можно разложить на совокупность гармонических сигналов с помощью преобразования Фурье. Рассмотрим непрерывный синусоидальный сигнал(переменную)с частотой f. Этот сигнал дискретизируется с частотой fs. Если выборка делается 6 раз за период изменения исходного непрерывного сигнала, то гладкая кривая проведенная через эти точки, близка к оригиналу и наблюдаемая частота f0 выходного сигнала не отличается от исходной f. Если делать выборку только три раза за период, то результирующая кривая менее точно может представлять входной сигнал, хотя наблюдаемая частота f0 сохраняется, равной f. Если исходный сигнал дискретизируется таким образом, что делается 5 выборок за 4 периода, то через полученные дискретные значения также можно провести плавную непрерывную кривую (синусоидальную), но наблюдаемая частота её f0 будет равна f/ /4. Наблюдаемая ложная частота f0 в этом случае есть разница между частотой выборки fs и и истинной частотой f исходного сигнала f0 = fs – f Данная особенность цифровых систем в случаях, когда частота выборки слишком мала по отношению к частотным составляющим исходного сигнала получила название транспонирования частот. Если выборка происходит один раз за период исходного сигнала, то очевидно, чтот исходный сигнал выбирается всегда в одной и той же фазе и для чисто периодического сигнала будет получаться одно и то же его значение. Другими словами наблюдаемая частота f0 становится нулевой (сигнал постоянен) и, если попытаться восстановить непрерывный сигнал по таким дискретным наблюдениям, то восстановленный сигнал будет постоянен. Очевидно, что для управления рассмотренная ситуация неприемлема, так как система управления «не видит» поведения объекта управления на данной частоте. Эффект транспонирования высокочастотной части спектра сигнала на низкочастотную особенно неприятен и опасен при возникновении на входе в системную ЦВМ высокочастотных помех с заранее неизвестными характеристиками. В этом случае транспонирование может произойти в ту часть спектра, которая характеризует управляемое движение объекта управления, где фильтрация помехи с помощью цифровых фильтров станет невозможной.
Математическое описание цифровых систем. Решетчатые функции.
Поскольку ввод информации в компьютер, а так же вывод информации из него может принципиально осуществляться только в дискретные моменты времени, а не непрерывно(ЦВМ – дискретное устройство), то необходимо разработать также специальный метод математического описания и анализа качества работы цифровых систем управления.
Описанная работа цифровых систем формализуется в структурную схему квантования по времени, который преобразует непрерывный сигнал r(t) в решетчатый сигнал r(kT).
Здесь kT – текущий момент замыкания, а функция δ(t) – дельта функция, имеющая математическое описание:
При этом Изображение по Лапласу δ(t) равно Δ(s)=1. Решетчатая функция получается из непрерывной функции r(t), если рассматривать только ее дискретные значения в моменты времени kT. Описание дискретного процесса только решетчатой функцией не совсем корректно и физически, и математически. Одной и той же решетчатой функции могут соответствовать несколько непрерывных функций, которые называются огибающими решетчатой функции. Этот эффект необходимо учитывать. Возникает иллюзия, что X управляется правильно, тогда как на самом деле величина Х может превышать допустимое значение. Экстраполятор нулевого порядка.
Вырезанный на момент kT сигнал в ЦВМ запоминается как входной (не меняется в течение времени T – такта и так каждый такт). Поэтому в динамической схеме системы необходимо учесть не только «вырезание» сигналов в моменты kT, но и запоминание их на этом уровне до момента следующего съема информации с датчиков и поступления её на обработку в процессор(k+1)T. Это запоминание реально осуществляемое в памяти ЦВМ, в которую введены данные, в нашей структурной схеме цифровых систем управления осуществляется специальным структурным элементом, который мы назовем экстраполятором нулевого порядка. Экстраполятор нулевого порядка «замораживает» значение снятой с датчиков и вводимой в ЦВМ информации до начала следующего съёма. Таким образом, дискретизация сигналов на входе и выходе управляющей ЦВМ моделируется сочетанием ключа и экстраполятора нулевого порядка.
Непрерывная r(t) заменяется дискретной ступенчатой rd(t). Передаточная функция экстраполятора нулевого порядка трансцендентна и имеет вид:
Методы декомпозиции СТС и их математических моделей, как средство уменьшения сложности проектирования СТС Содержание концепции декомпозиции состоит в том, что при проектировании и исследовании СТС в первую очередь выявляется её внутренняя структура, характер связей между частями или элементами с целью свести по возможности исходную задачу исследования СТС к совокупности частных задач исследования её составных частей по возможности слабосвязанных. Цель декомпозиции – снизить сложность представления устройства системы, сложность её поведения и сложность представления её работы для разработчика пользователя и заказчика. Каждая выделенная при декомпозиции часть проще для восприятия, описания поведения, проектирования, изготовления и эксплуатации. После чего объединение выделенных частей в целое также упрощается поскольку при этом можно абстрагироваться от деталей устройства каждой из них, сосредоточившись только на вопросах их взаимодействия. В математике реализация принципа декомпозиции связана, как правило, с приемом замены переменных. Поэтому не удивительна та роль, которая отводится в науке управления поиску рациональных преобразований математических моделей и выражений, позволяющих разделить вектор состояния сложной системы на независимые части. Менее строгий, но также широко применяемый прием декомпозиции состоит в искусственном, но обоснованном упрощении математических моделей, что позволяет ослабить или полностью исключить связи между некоторыми их частями и создать тем самым предпосылки для разделения СТС на независимые части. При этом надо учитывать, что декомпозиция не нарушает целостности системы. Т.е. декомпозированная система не ведро подсистем, а целостный объект, допускающий членения. Начнем с широко применяемого в теории управления мехатронными СТС подхода, связанного с представлением модели движения СТС в виде двух моделей: моделей возмущенного и невозмущенного движения. В большинстве случаев такая декомпозиция оправдана и упрощает исследование: исходная задача разбивается на две решаемые последовательно. Первая задача исследует закономерности идеализированного невозмущенного движения, а вторая учитывает действие возмущений на уже определенное невозмущенное движение. Физическая основа такой декомпозиции разделение системы на части, имеющие сильно отличающиеся собственные частоты. В этом случаи влияние на медленно меняющие составляющие быстро меняющихся осредняется. А влияние на быстроменяющиеся части медленно меняющихся эквивалентно наличию каких-то постоянных возмущений или заданию медленноменяющейся программы. Например, этот принцип декомпозиции реализуется применительно к системам управления подвижными объектами типа ракет, кораблей и т.п. в виде разделения общей задачи управления на две задачи, которые назовем задачами наведения и стабилизации. Суть данной декомпозиции – выделить из общей задачи управления движением задачу программирования движения центра масс объекта и углового движения относительно центра масс объекта для попадания в заданную цель и задачу отработки найденных программ управления в том числе и по углу с парированием возмущающих воздействий, препятствующих выполнению найденных программ (задачу стабилизации). Системы стабилизации движения строятся и функционируют как замкнутые системы автоматического управления, целью управления которых является сведение к нулю отклонений между заданным системой наведения движением и фактическим движением, определяемым измеренными значениями соответствующих параметров движения. Здесь примером может служить управление движением корабля: одни люди (капитан или штурман) прокладывают курс и задают направление движения, а рулевой просто выдерживает заданный курс, борясь с ветром, волнами и т.п. Даже, если рулевой и штурман это один человек, что бывает часто на небольших судах, эти задачи все равно решаются раздельно, как бы раздвоением личности. В соответствии с перечисленными функциями система управления ракетой, которая по всем признакам является СТС, может быть разделена на три взаимосвязанные подсистемы: Навигационно- измерительную систему, Систему наведения, Систему стабилизации движения. На рис.2 приведена схема системы управления движением СТС, вытекающая из данной декомпозиции.
Рис2 Схема системы управления движением ракеты
Дальнейшее применение принципа декомпозиции связано с использованием, так называемого, «развязанного управления» - независимого управления многосвязным объектом по отдельным каналам. Принцип развязанного управления может быть использован не всегда, а только при наличии особых предпосылок в динамических свойствах и устройстве объекта управления. Строго говоря главным динамическим свой ством объекта для развязного управления являются наличие слабых межканальных связей и возможность использования принципа суперпозиции, что характерно для линейных систем. Возможность линеаризации уравнений объекта управления при малых отклонениях от опорного движения позволяет провести декомпозицию и разделить задачу управления полетом ракеты на задачу управления поступательным движением ц.м. и на задачу управления угловым движением относительно ц.м. Далее движение ц.м. можно разделить на три движения в взаимно перпендикулярных плоскостях продольной, боковой и поперечной. При малых отклонениях движения РН от опорного эти три движения оказываются практически независимыми. Это в частности позволяет строить наведение и систему стабилизации в виде трех независимых каналов. Однако при больших отклонениях движения от опорного, что бывает при нештатных ситуациях, нарушаются условия линеаризации и не связанности каналов т.е. они влияют друг на друга и раздельное движение не реализуется. В этих случаях необходимо рассмотрение пространственного движения объекта управления. Таким образом, декомпозиция объекта управления с разделением на плоские каналы тангажного углового движения, движения в плоскости рыскания, продольного движения и углового движения относительно продольной оси может проводиться для большинства задач, не связанных с пространственным движением и большими отклонениями от программного движения на активных участках траектории. Лекция 7. Пример СТС, управляемой от встроенной ЦВМ. Метод Эйлера численного интегрирования уравнений управления СТС.
Пример системы управления с ЦВМ в контуре управления. Уравнения объекта управления
Для примера реальной системы, управляемой ЦВМ, рассмотрим цифровую систему управления ракеты. При этом для начала пренебрежем эффектами квантования по времени и по уровню в бортовой управляющей ЦВМ. Получим линеаризованное описание отклонения ракеты по угловому положению от заданного, например, по каналу тангажа. Ракета в процессе полета находится в сложном пространственном движении ее центра масс и угловом движении относительно центра масс. Доказано, что движение центра масс ракеты по траектории мало зависит от ее углового движения,если угловые отклонения ракеты устойчивы и малы. Движение центра масс ракеты связано с угловым её движением относительно центра масс только в связи с изменением параметров уравнений объекта управления из-за изменений момента инерции в связи с расходом топлива и изменением аэродинамических сил в связи с изменениями высоты и скорости полета ракеты. Эти изменения известны заранее при полете ракеты по заданной траектории и могут быть учтены при при проектировании в расчете параметров модели углового движения ракеты. Это позволяет рассматривать движение ц.м. ракеты независимо от ее углового движения относительно ц.м. и наоборот. При описании динамики объектов управления мехатронных систем краеугольным камнем является второй закон Ньютона. Для применения 2-го закона Ньютона необходимо задать некоторую систему координат, относительно которой будут определяться ускорение, скорость, положение, направление сил, действующих на объект. Нам известен закон в форме:
здесь F – вектор сил, действующих на объект.
Применительно к плоскому вращательному движению объекта относительно точки центра масс (ц.м.) в плоскости тангажа 2-ой Закон Ньютона записывается в виде
Здесь Jо – момент инерции относительно центра вращения(ц.м.).
M – момент сил, действующих относительно центра масс. Рассмотрим две системы прямоугольных координат с началом в одной точке – центре масс ракеты(ц.м.). Одну систему координат назовем связанной - она совпадает с осями ракеты. Другую систему координат назовем скоростной. В этой системе координат ось Х совпадает с вектором скорости ракеты. В невозмущенном движении ракеты вертикально при отсутствии ветра направления осей этих систем координат совпадают. При возмущениях, приводящих к угловым эволюциям ракеты, или при программном изменении углового положения продольной оси ракеты при ее движении к орбите выведения спутника между осями этих систем координат т.е между продольной осью ракеты и вектором скорости ракеты имеется угол Линеаризованное уравнение, полученное при малости отклонений угла тангажа от заданной величины, описывающее угловое движение ракеты по каналу тангажа на первой ступени полета.
Здесь:
Мв – возмущающий момент от неточности изготовления и сборки ракеты; α – угол атаки – угол между продольной осью ракеты и направлением набегающего потока; J – момент инерции ракеты относительно ее ц. м.; хт – положение центра масс; хд – положение центра давления аэродинамических сил, (хт - хд) – плечо аэродинамической силы относительно центра масс ракеты
Разделим левую и правую часть равенства на J. Тогда, обозначая
Данная модель углового движения ракеты упрощена. Отсутствуют динамические члены уравнения, связанные с упругостью корпуса и с подвижностью топлива в баках. Кроме того мы не будем учитывать изменение во времени параметров уравнения – уменьшение Jz за счет расхода топлива, изменения Значения коэффициентов уравнения углового движения ракеты принимались постоянными и равными Сυυ = - 0,6 1/сек2 (ракета статически неустойчива – центр давления ближе к носу ракеты, чем центр масс) Сυδ = 1 1/сек2 Мв = 0,2 1/сек2
Закон управления, учитывающий скорость изменения управляемой координаты
Линеаризованное описание отклонения ракеты по угловому положению от заданного по каналу тангажа и описание поведения управляющего устройства, имеет вид:
τ
Здесь υ- отклонения угла тангажа от заданного положения δ - отклонение управляющего органа (управляющего двигателя ракеты) Параметр τ определяет запаздывание в управляющем устройстве, определяемое инерционностью привода и управляющего двигателя, а параметр Т=а1/а0 определяет опережение по фазе, связанное с использованием в законе управления сигнала, пропорционального угловой скорости вращения ракеты по тангажу. Запаздывание τ в управляющем устройстве (в контуре обратной связи (ОС)) катастрофически будет влиять на устойчивостьуглового движения ракеты. Это запаздывание приводит к раскачке ракеты - подталкиванию запаздывающим управляющим воздействием в фазу угловых колебаний вместо желаемого притормаживания. Запаздывание в контуре ОС можно парировать, внося упреждение в сигнал, выдаваемый на ИО. Это предвидение – упреждение появляется, если учитывать скорость изменения управляемой координаты. Для мехатронной СТС – это означает использование вместе с датчиком угла датчика угловой скорости. Можно, конечно, дифференцировать сигнал угла, но операция дифференцирования всегда затруднительна в практической реализации из-за наличия помех в сигнале тангажа, которые операцией дифференцирования «подчеркиваются». Таким образом, управление ракетой в канале тангажа осуществляется по угловому отклонению и скорости изменения этого отклонения. Учет скорости изменения управляемой координаты обеспечивает предсказание ее поведения на ближайшем интервале времени т. е. компенсирует запаздывания в контуре управления.
Действительно, если имеет место отклонения
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 636; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.55.193 (0.014 с.) |


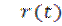
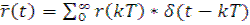

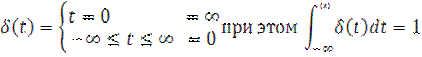
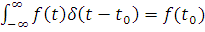 . Дельта функция вырезает в данном выражении значение f в момент to.
. Дельта функция вырезает в данном выражении значение f в момент to.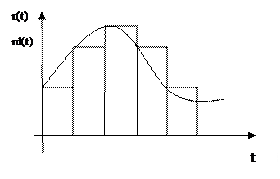

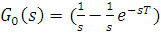 это разность двух сдвинутых единичных функций.
это разность двух сдвинутых единичных функций.
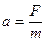 или
или 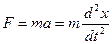 ,
,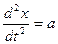 - вектор ускорения.
- вектор ускорения.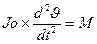
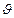 - угол поворота ракеты в плоскости тангажа.
- угол поворота ракеты в плоскости тангажа.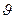 , который и является в данном случае углом атаки набегающего потока. Аэродинамическая сила,действующая на ракету, является функцией этого угла. Зависимость аэродинамических сил от угла атаки нелинейна, но при малых углах атаки может быть линеаризована.
, который и является в данном случае углом атаки набегающего потока. Аэродинамическая сила,действующая на ракету, является функцией этого угла. Зависимость аэродинамических сил от угла атаки нелинейна, но при малых углах атаки может быть линеаризована.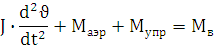
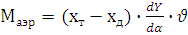 - аэродинамический момент относительно центра масс;
- аэродинамический момент относительно центра масс;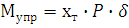 - управляющий момент от поворота двигателя;
- управляющий момент от поворота двигателя;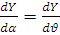 – производная аэродинамических сил по углу атаки.
– производная аэродинамических сил по углу атаки.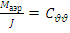 и
и 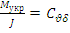 ,имеем запись уравнения углового движения в угловых ускорениях:
,имеем запись уравнения углового движения в угловых ускорениях: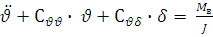
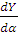 за счет изменения скорости и высоты полета.
за счет изменения скорости и высоты полета.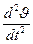 + Сυυ υ + Сυδ δ = Мв
+ Сυυ υ + Сυδ δ = Мв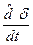 + δ = а0 υ + а1
+ δ = а0 υ + а1 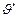
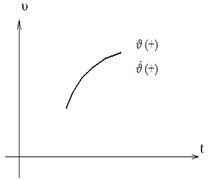
 , но оно уменьшается, за счет набранной ракетой угловой скорости противоположного знака, то управляющее воздействие не должно быть чрезмерным, чтобы не вызвать перерегулирования. И обратно, если
, но оно уменьшается, за счет набранной ракетой угловой скорости противоположного знака, то управляющее воздействие не должно быть чрезмерным, чтобы не вызвать перерегулирования. И обратно, если 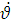 имеют один знак, надо тормозить энергично нарастающее отклонение ракеты от заданного положения.
имеют один знак, надо тормозить энергично нарастающее отклонение ракеты от заданного положения.


