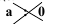Закон 1. Переместительный закон сложения.

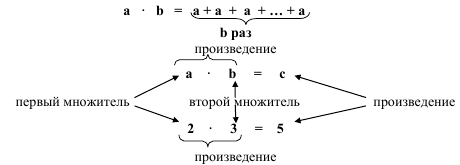
От перемены мест слагаемых значение суммы не меняется:

a + b = b + a

4 + 2 = 2 + 4

Закон 2. Сочетательный закон сложения.

Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел или ко второму числу прибавить сумму первого и третьего чисел:

(a + b) + c = a + (b + c) = (a + c) + b

(2 + 4) + 8 = 2 + (4 + 8) = (2 + 8) + 4

УМНОЖЕНИЕ

Умножение - это сложение одинаковых слагаемых.

2 + 2 + 2 = 2 · 3 = 6

2 – слагаемое

3 – число, которое показывает, сколько раз повторяется слагаемое 2 (по два три раза)

•, х - знаки умножения.

 

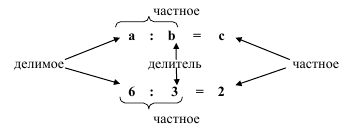
ДЕЛЕНИЕ

Деление - это действие, обратное умножению.

6: 2 = 3 6: 3 = 2

ЗАКОНЫ УМНОЖЕНИЯ

Закон 1. Переместительный закон умножения

От перестановки множителей произведение не меняется:

a · b = b · a

4 · 2 = 2 · 4

8 = 8

Закон 2. Сочетательный закон умножения

Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел или второе число умножить на произведении первого и третьего чисел:

(a · b) · c = a · (b · c) = (a · c) · b

(2 · 4) · 8 = 2 · (4 · 8) = (2 · 8) · 4

Закон 3. Распределительный закон умножения.

Относительно сложения

Произведение суммы на число равно сумме произведений каждого слагаемого на это число.

(a + b + c) · d = a · d + b · d + c · d

(2 + 5 + 3) · 2 = 2 · 2 + 5 · 2 + 3 · 2 = 20

Относительно вычитания

Чтобы умножить разность на число, достаточно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе произведение.

(a - b) · d = a · d - b · d

(15 - 5) · 4 = 15 · 4 - 5 · 4 = 60 -+ 20 = 40

 

СВОЙСТВА ДЕЛЕНИЯ

Правило 1. Чтобы разделить сумму на число, достаточно разделить каждое слагаемое на это число, а полученные результаты сложить.

(a + b): c = a: c + b: c

Правило 2. Чтобы разделить разность на число, достаточно разделить на это число уменьшаемое и вычитаемое, а затем из первого частного вычесть второе частное.

(a - b): c = a: c - b: c

Правило 3. Частное от деления произведений двух множителей на число равно произведению одного из множителей на частное от деления второго множителя на это число.

(a · b): c = (a: c) · b = a · (b: c)

Правило 4. Чтобы разделить число на частное, достаточно разделить это число на делимое и полученный результат умножить на делитель.

a · (b: c) = (a: b) · c

Правило 5. Чтобы разделить частное на число, достаточно умножить делитель на это число и разделить делимое на полученный результат Можно так же разделить делимое на это число, а полученный результат разделить на делитель.

(a: b): c = a: (b · c)

или

(a: b): c = (a: c): b

 

НАХОЖДЕНИЕ КОМПОНЕНТОВ ДЕЛЕНИЯ

Правило. Чтобы найти неизвестный делитель, нужно делимое разделить на частное.

a:? = c? = a: c

Чтобы найти неизвестное делимое, нужно частное умножить на делитель.

?: b = c? = c · b

 

ТАБЛИЦА УМНОЖЕНИЯ ПИФАГОРА

 

ОСОБЫЕ СЛУЧАИ УМНОЖЕНИЯ

a · 1 = a 1 · a = a

4 · 1 = 4 1 · 4 = 4

 

0 · a = 0 a · 0 = 0

0 · 6 = 0 6 · 0 = 0

 

ОСОБЫЕ СЛУЧАИ ДЕЛЕНИЯ

a: 1 = a

8: 1 = 8

0: a = 0

0: 6 = 0

a: a = 1

8: 8 = 1

 

На нуль делить НЕЛЬЗЯ!

Нуль можно делить на любое число, получится 0.

 

ПРИЗНАКИ ДЕЛИМОСТИ

На 2 делятся все чётные числа, то есть числа, которые оканчиваются цифрами 0, 2, 4, 6, 8.

На 3 делятся все числа, сумма цифр которых делится на 3.

На 5 делятся все числа, которые оканчиваются на 0 или 5.

На 6 делятся числа, которые делятся одновременно и на 2, и на 3.

На 9 делятся числа, сумма цифр которых делится на 9.

 

ИМЕНОВАННЫЕ ЧИСЛА

Именованные числа – это числа, полученные при измерении величин и сопровождающиеся названием единиц измерения.

Например: 2 кг, 4 см, 8 л.

Именованные числа бывают простые и составные.

Простые именованные числа: 7 м, 18 т, 21 кг – в них входит только одна единица измерения.

Составные именованные числа: 2 м 4 см, 24 кг 45 г, 8 км 520 м – в них входят несколько единиц измерения.

 

ПРЕОБРАЗОВАНИЕ ИМЕНОВАННЫХ ЧИСЕЛ

Чтобы перейти от одних единиц измерения к другим, пользуйся таблицей величин.

 

Таблица величин 1 см = 10 мм 1 дм =10 см 1 м = 10 дм = 100 см = 1000 мм 1 км = 1000 м = 10000 дм = 100000 см	Единицы измерения массы 1 кг = 1000 г 1 ц = 100 кг 1 т = 10 ц = 1000 кг
Единицы измерения времени 1 мин = 60 с 1 ч = 60 мин = 3600 с 1 сутки = 24 часа 1 неделя = 7 дней 1 месяц = 30 или 31 день (в феврале 28 или 29 дней) 1 год = 12 месяцев = 52 недели = 365 или 366 дней 1 век (столетие) = 100 лет	Единицы измерения площади 1 мм^2 1 см^2 = 100 мм^2 1 дм^2 = 100 см^2 1 м^2 = 100 дм^2 = 10000 см^2 1 км^2 = 1000000 м^2 1 ар (1 а) = 1 сотка = 100 м^2 1 гектар (1 га) = 10000 м^2