
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Переходные процессы в электрических цепяхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Всякий режим, длительно существующий в электрической цепи и характеризующийся неизменными значениями токов и напряжений, называется стационарным (установившимся) режимом. Такому режиму соответствует определённый запас энергии, сосредоточивающийся в реактивных элементах цепи – индуктивностях и ёмкостях. Любые изменения нагрузки или напряжения источника питания (включение или выключение его) приводят в итоге к новому установившемуся режиму с другими значениями токов, напряжений и, следовательно, запасом энергии в реактивных элементах. Переход от одного стационарного состояния к другому называется переходным (нестационарным) процессом, который связан с изменением запаса энергии. Всякое изменение запаса электрической или магнитной энергии не может происходить мгновенно, а сопровождается процессом установления нового энергетического режима в цепи. При воздействии на вход электрической цепи импульсов с крутым фронтом без особых погрешностей можно полагать, что воздействие этого импульса на электрическую цепь происходит скачкообразно, подобно мгновенному включению или выключению напряжения (тока). Теоретически можно считать, что коммутация цепи (т.е. изменение параметров цепи или схемы самой цепи) происходит мгновенно, т.е. на включение и выключение цепи время не расходуется. Тем не менее, переход от одного режим работы цепи к другому происходит не мгновенно, а в течение некоторого промежутка времени. Объясняется это тем, что каждому состоянию цепи соответствует определённый запас энергии электрических и магнитных полей. Переход к новому режиму связан с нарастанием или убыванием энергии этих полей. Энергия магнитного поля
и электрического поля
не может мгновенно изменяться, энергия может изменяться только плавно. Если попытаться предположить обратное, то на индуктивности появилось бы бесконечно большое напряжение:
(где
Аналогично невозможно себе представить скачкообразное изменение электрического поля ёмкости, так как в противном случае через ёмкость должен был бы протекать бесконечно большой ток
что также лишено физического смысла. Наконец, известно, что мощность Ясно, что этого быть не может. Свойство реактивных элементов цепи (L и C) запасать или расходовать определённую энергию в конечный промежуток времени характеризует их электрическую инерционность. Именно это свойство реактивных элементов цепи и лежит в основе переходных процессов. В линейных цепях, не содержащих реактивных элементов, переходные процессы отсутствуют. Для количественной характеристики длительности переходных процессов в простых электрических цепях, содержащих комбинации R, L и C вводится понятие постоянной времени (τ). Этот параметр имеет размерность времени (с). Сущность параметра τ можно показать на примере цепей, в которых переходные процессы имеют ярко выраженный экспоненциальный характер (рис.1.1).
Рис.1.1. Цепь RС с экспоненциальным зарядом конденсатора
Такие электрические цепи обязательно содержат реактивные элементы L или C, а также активное сопротивление R. Так, для цепи заряда ёмкости C от мгновенного включения источника постоянного напряжения Uвх = Е (рис.1.1)закон изменения тока заряда ёмкости имеет вид:
Напряжение на выходе цепи
(Это выражение получается при математическом анализе переходного процесса в данной цепи; мы даём его без вывода). Выражение (1.4) называется экспоненциальной функцией. Другая её запись:
Произведение
называется постоянной времени цепи. Особенностью этой функции является то, что при t ≥ 0 она монотонно убывает. Все значения этой функции положительны. Максимальное значение функции Постоянная времени
Рис.1.2. Закон изменения напряжения на ёмкости цепи, изображённой на рис.1.1.
Напряжение на ёмкости изменяется по экспоненциальному закону
Если же напряжение (ток) уменьшается от какого-либо уровня (в том числе и от максимального), то постоянная времени численно равна времени, в течение которого сигнал экспоненциально убывает примерно до 37% от своего максимума (рис.1.3).
Рис.1.3. Закон изменения тока, протекающего через ёмкость цепи, изображённой на рис.1.1.
Ток, протекающий через ёмкость, изменяется по экспоненциальному закону:
В справедливости выражений (1.7) и (1.8) легко убедиться, подставляя в них последовательно значения t = τ; t = 2τ; t = 3τ и т.д. (табл.1.1): Табл.1.1.
Отсюда следует вывод, что для окончания переходного процесса требуется время t = (3…5) τ ………………………………... (1.9). За это время любой переходный процесс прекращается на (95…99)%. Таким образом, мы убедились в том, что для переходного процесса требуется вполне конкретное время, определяемое длительностью импульса, действующего на входе цепи, и параметрами этой цепи. Тем не менее, в импульсной технике принимают следующие допущения, позволяющие упростить анализ электрических цепей с сосредоточенными параметрами. Эти допущения носят название законов коммутации: 1. Токи, протекающие через конденсаторы и резисторы, могут изменяться скачкообразно. 2. Напряжения на индуктивностях и резисторах могут изменяться скачкообразно. Первый закон коммутации можно объяснить следующим образом. Известно, что ток, протекающий через ёмкость, и напряжение на этой ёмкости связаны следующими соотношениями:
и Из выражения (1.11) следует, что при любом конечном изменении тока ic(t), заряжающего конденсатор, напряжение на нём скачком изменяться не может. Аналогично можно объяснить второй закон коммутации. Известно, что напряжение, приложенное к индуктивности, и протекающий через неё ток связаны следующими соотношениями:
и Из выражения (1.13) следует, что при любом конечном изменении напряжения на индуктивности ток через неё скачком изменяться не может. Наличие переходных процессов является причиной искажения формы импульсов, действующих в линейной цепи. Если бы все процессы в цепи устанавливались мгновенно, то никаких искажений импульсов в линейной цепи не было бы.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 1199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.13.196 (0.012 с.) |

 ………………………(1.1)
………………………(1.1)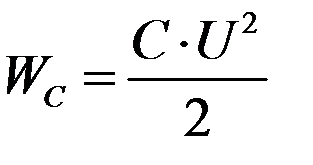 …………………….. (1.2)
…………………….. (1.2) ,
, – поток магнитной индукции), что лишено физического смысла так как
– поток магнитной индукции), что лишено физического смысла так как при dt → 0.
при dt → 0. при dt → 0,
при dt → 0, . Если предположить, что запасённая в реактивном элементе энергия может изменяться скачком, то при условии dt → 0 мощность должна достигать бесконечно больших значений, а это возможно было бы при внутреннем сопротивлении источника Ri = 0.
. Если предположить, что запасённая в реактивном элементе энергия может изменяться скачком, то при условии dt → 0 мощность должна достигать бесконечно больших значений, а это возможно было бы при внутреннем сопротивлении источника Ri = 0.
 ……………………………(1.3).
……………………………(1.3). …………………. (1.4).
…………………. (1.4). ……………………… (1.5).
……………………… (1.5). ……………………………………… (1.6)
……………………………………… (1.6)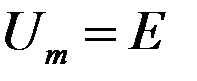 соответствует моменту времени
соответствует моменту времени  . Минимальное значение функции равно нулю при
. Минимальное значение функции равно нулю при  и является предельным её значением. Стремление функции к этому значению происходит асимптотически. Для достижения предельного значения требуется бесконечно большое время.
и является предельным её значением. Стремление функции к этому значению происходит асимптотически. Для достижения предельного значения требуется бесконечно большое время. характеризует скорость установления стационарного режима в цепи, т.е. скорость переходного процесса. Численно постоянная времени равна времени, в течение которого амплитуда напряжения (тока) в цепи изменяется в е раз (е ≈ 2,72). Если напряжение (ток) возрастает от какого-либо уровня (в том числе и от нулевого), то постоянная времени численно равна интервалу времени, в течение которого экспоненциально возрастающий сигнал достигает примерно63%своей максимальной величины (рис.1.2).
характеризует скорость установления стационарного режима в цепи, т.е. скорость переходного процесса. Численно постоянная времени равна времени, в течение которого амплитуда напряжения (тока) в цепи изменяется в е раз (е ≈ 2,72). Если напряжение (ток) возрастает от какого-либо уровня (в том числе и от нулевого), то постоянная времени численно равна интервалу времени, в течение которого экспоненциально возрастающий сигнал достигает примерно63%своей максимальной величины (рис.1.2).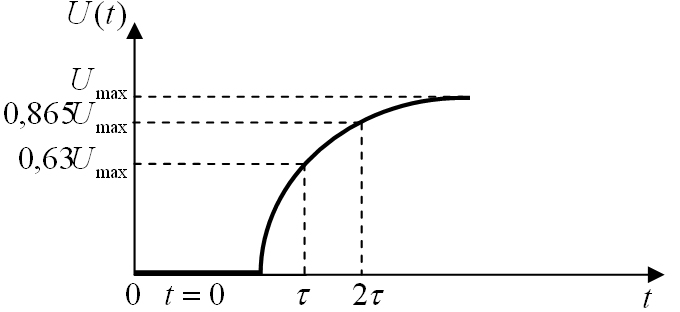

 ………………………… (1.7).
………………………… (1.7).
 ……………………………. (1.8).
……………………………. (1.8).


 …………………………...... (1.10)
…………………………...... (1.10) ……………………(1.11).
……………………(1.11). ………………………….... (1.12)
………………………….... (1.12) ……………….... (1.13).
……………….... (1.13).


