
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Круговые и переходные кривыеСодержание книги
Поиск на нашем сайте
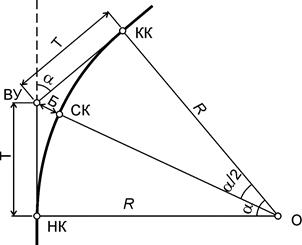
Круговые кривые. Железнодорожные линии (также и автомобильные дороги) в плане состоят из прямолинейных участков, сопряжённых между собой кривыми. Наиболее простой и распространённой формой кривой является дуга окружности. Такие кривые носят название круговых кривых. На железных дорогах применяют круговые кривые со следующими радиусами: 4000, 3000, 2000, 1800, 1500, 1200, 1000, 800, 700, 600, 500, 400 и 300 м. Радиус кривой выбирают при проектировании дороги, руководствуясь конкретными техническими условиями. Главными точками кривой, определяющими её положение на местности, являются вершина угла ВУ, начало кривой НК, середина кривой СК и конец кривой КК (рис. 15.3).
Рис. 15.3 Схема круговой кривой
Основные элементы кривой – её радиус R и угол поворота a. К основным элементам относятся также: – тангенс кривой Т (или касательная) - отрезок прямой между вершиной угла и началом или концом кривой; – кривая К - длина кривой от начала кривой до её конца; – биссектриса кривой Б - отрезок от вершины угла до середины кривой; – домер Д - разность между длиной двух тангенсов и кривой. Во время изысканий угол a измеряют, а радиус R назначают. Остальные элементы вычисляют по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НК, О (центр окружности): Т = R ×tg(a/2); К = R ×a = p R a°¤180°; Б = R [sec(a/2) - 1], (15.1) где a° - угол поворота в градусах. Домер вычисляют по формуле
Вместо вычислений по формулам можно воспользоваться таблицами для разбивки кривых на железных дорогах, где по заданным радиусу и углу поворота сразу находят значения Т, К, Б и Д. В месте поворота трассы пикетаж ведётся по кривой. Пикетажное положение главных точек кривой определяют по формулам: ПК НК = ПК ВУ - Т; ПК КК = ПК НК + К; ПК СК = ПК НК + К/2. (15.3) Правильность вычислений контролируют по формулам: ПК КК = ПК ВУ + Т - Д; ПК СК = ПК ВУ + Д/2. (15.4) Пример. Измерено a = 18°19¢ и задан радиус R = 600 м. Вершина угла расположена на пикете 6 + 36,00. По формулам (15.1) и (15.2) или по таблицам находим элементы кривой: Т = 96,73 м; К = 191,81 м; Д = 1,65 м; Б = 7,75 м. Вычислим пикетажное положение главных точек: Контроль: ПК ВУ 6 + 36,00 ПК ВУ 6 + 36,00 - Т 96,73 + Т 96,73 ПК НК 5 + 39,27 7 + 32,73 + К 1 + 91,81 - Д 1,65 ПК КК 7 + 31,08 ПК КК 7 + 31,08
ПК НК 5 + 39,27 ПК ВУ 6 + 36,00 + К/2 95,90 - Д/2 0,82 ПК СК 6 + 35,17 ПК СК 6 + 35,18 Переходные кривые. Непосредственное сопряжение прямого участка пути с круговой кривой приводит к тому, что во время движения поезда в месте сопряжения внезапно возникает центробежная сила F, прямо пропорциональная квадрату скорости движения v и обратно пропорциональная радиусу кривой
где s и r - текущие значения расстояния от начала переходной кривой и ее радиуса кривизны; R – радиус кривизны в конце переходной кривой. Индексом k отмечены значения переменных в конце переходной кривой. Для радиуса кривизны переходной кривой в текущей точке i найдём: r = lR / s, (15.5) где через l обозначена длина переходной кривой sk. Кривая, описываемая уравнением (15.5), в математике называется клотоидой, или радиоидальной спиралью. Угол поворота трассы на переходной кривой. На бесконечно малом отрезке кривой ds (рис. 15.4, а) происходит поворот трассы на угол
Подставляя выражение радиуса кривизны r из (15.5), получим
Выполним интегрирование от начала кривой НК, где j = 0 и s = 0, до текущей точки i:
откуда Rl j = s 2/2.
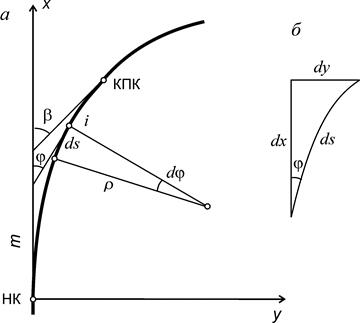
Рис. 15.4 Схема переходной кривой: а – углы поворота трассы: φ – в текущей точке i, β – в конце переходной кривой (точка КПК); б - приращения координат
Из полученного уравнения вытекают формулы:
где b - угол поворота трассы в конце переходной кривой; l - длина переходной кривой; R - радиус кривизны в конце переходной кривой, равный радиусу следующей за нею круговой кривой. Координаты точки переходной кривой. Совместим начало координат с началом переходной кривой и направим ось x по касательной к ней (см. рис. 15.4, а). Бесконечно малому приращению дуги кривой соответствуют бесконечно малые приращения координат (рис. 15.4, б): dx = cosj× ds; dy = sinj× ds. (15.7) Разложим синус и косинус в ряд и, удержав в разложениях по два члена, подставим в них выражения для j из (15.6): cosj = 1-j2/2 = 1 - s 4/(8 R 2 l 2); sinj = j - j3/6 = s 2/(2 Rl) - s 6/(48 R 3 l 3). Подставляя полученные выражения в (15.7) и выполняя интегрирование, найдём:
Смещение начала кривой (сдвижка). На рис. 15.5 дуга НК-КПК представляет собой переходную кривую, переходящую после точки КПК в круговую. Продолжим круговую кривую до точки Q, где её направление, параллельно оси x. Обозначим через m смещение, параллельное оси x, начала переходной кривой относительно точки Q, в которой начиналась бы круговая кривая при отсутствии переходной. Через p обозначим смещение в перпендикулярном направлении. Из рис. 15.5 видно:
где x КПК и y КПК - координаты конца переходной кривой, вычисляемые по формулам (15.8) и (15.9) с аргументом s = l. Сочетание круговой кривой с переходными. На рис. 15.6 показана кривая, поворачивающая трассу на угол a и состоящая из круговой части с радиусом R и двух переходных кривых одинаковой длины l.
Если бы не было переходных кривых, в образованный прямыми линиями трассы угол была бы вписана дуга окружности радиуса R, равная Q -СК- Q 1 и имеющая длину K = R a. При наличии переходных кривых на каждой из них происходит поворот трассы на угол b, отчего на долю круговой кривой приходится поворот на угол a-2b. Поэтому суммарная длина кривой равна Kc = R (a-2b) + 2 l = R a - 2 R b + 2 l = K - l + 2 l = K + l. Тангенс и биссектриса определяются по формулам: Тс = T + m + T p; Бc = Б + Б p, где Т p = p tg(a/2); Б p = p sec(a/2). Домер в этом случае равен
В полевых условиях значения m,Т p и Б p вычисляют на микрокалькуляторе или выбирают из таблиц для разбивки кривых на железных дорогах. Пикетажное положение главных точек кривой вычисляют по формулам, аналогичным (15.3) и (15.4).
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 756; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.122.140 (0.009 с.) |

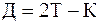 . (15.2)
. (15.2)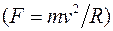 . Чтобы обеспечить постепенное нарастание центробежной силы, между прямой и круговой кривой вставляют переходную кривую, радиус кривизны r которой плавно изменяется от ¥ до R. Если положить, чтобы центробежная сила менялась пропорционально расстоянию s от начала кривой, то получим
. Чтобы обеспечить постепенное нарастание центробежной силы, между прямой и круговой кривой вставляют переходную кривую, радиус кривизны r которой плавно изменяется от ¥ до R. Если положить, чтобы центробежная сила менялась пропорционально расстоянию s от начала кривой, то получим ,
, .
.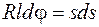 .
. ,
, ;
;  ; l = 2 R b, (15.6)
; l = 2 R b, (15.6)
 ; (15.8)
; (15.8)
 . (15.9)
. (15.9) ,
,

 .
.


