
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Сигналы импульсных устройствСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Введение Импульсная техника занимается изучением методов и средств получения и преобразования импульсов, а также управления ими. Задачи, стоящие перед импульсной техникой, выдвигаются потребностями практики в связи с множеством различных применений импульсных методов. Импульсная техника является составной частью радиоэлектроники и служит, в частности, базой радиолокации, телевидения, радионавигации, многоканальной связи, компьютерной техники и др. К областям науки и техники, где эффективно используются импульсные методы, относятся также телеуправление, измерение электрических и неэлектрических величин, кодированная радиосвязь, промышленная автоматика. В последние несколько десятилетий импульсная техника обогатилась новой областью – цифровой техникой – основой электронных цифровых вычислительных машин, станков с ЧПУ, роботов, сотовых телефонов, цифрового телевидения и т.п. С развитием цифровой техники на новую качественную ступень перешли средства связи, радиолокация, управление предприятиями и целыми отраслями народного хозяйства, комплексов для обработки различных видов информации. Этому в немалой степени способствовали разработка и создание новой элементной базы, что привело к резкому снижению габаритов и массы радиоэлектронной аппаратуры. На основе импульсной техники идёт бурное развитие новых поколений телевизионной, радиовещательной техники, спутниковых радионавигационных систем, радиолокационных систем и др. Импульсная техника решает разнообразные задачи, основными из которых являются: 1. Формирование импульсов с помощью линейных и нелинейных электрических цепей. При этом из синусоидальных колебаний и различных импульсов формируются импульсы необходимой формы, длительности и полярности. 2. Генерирование импульсов релаксационными генераторами с самовозбуждением и с посторонним запуском. Параметры генерируемых импульсов определяются типом генератора и параметрами его схемы. 3. Управление импульсами, что включает синхронизацию генераторов импульсов и временнýю задержку импульсов, т.е. вопросы, связанные с управлением временн ы м положением импульсов, а также вопросы счёта импульсов.
Глава 1. Сигналы импульсных устройств Общие сведения Сигналом называют физический процесс, несущий информацию. Сигналы могут быть звуковыми, световыми, электрическими. Информация сосредоточена в изменениях параметров физического процесса. Если параметры процесса не меняются, то он не является сигналом. Так, например, неизменный по тональности и громкости звук, световой поток или синусоидальное электрическое колебание с постоянной амплитудой или частотой никакого сообщения не содержат. Наоборот, в изменениях громкости и тона звука, яркости и цвета светового излучения, амплитуды, частоты или фазы электрического колебания запечатлена информация. Информативным является также появление или окончание, например, электрического колебания, т.е. его изменения. Сигналы на выходе микрофона, передающей ТВ- камеры, различного рода датчиков аналогичны по своему «рисунку» воздействиям на эти устройства – звуковому давлению, распределению освещённости, температуре и т.п. Поэтому подобные сигналы называют аналоговыми. Между минимальным и максимальным значениями аналоговый сигнал может иметь любое значение. Обычно аналоговые сигналы являются непрерывными. Устройства, в которых производится обработка таких сигналов, называются аналоговыми. Расстояние, на которое передаётся электрический сигнал, может быть как весьма малым (в пределах устройства), так и весьма большим (например, при исследовании космического пространства). По физическим линиям связи (проводам) электрические сигналы могут передаваться в том виде, в каком они снимаются с источника. При передаче сигнала через открытое пространство производят модуляцию информационным сигналом высокочастотное колебание, за счёт чего обеспечиваются эффективное излучение и приём сигнала. Информация, которую переносит сигнал, может являться сообщением о событии, о режиме технологического процесса, представлять команду на включение или выключение какой-либо аппаратуры и т.д. Переданная информация может быть выражена различным образом: речью, изображением, звуком, электрическим колебанием.
Табл.1.1.
Отсюда следует вывод, что для окончания переходного процесса требуется время t = (3…5) τ ………………………………... (1.9). За это время любой переходный процесс прекращается на (95…99)%. Таким образом, мы убедились в том, что для переходного процесса требуется вполне конкретное время, определяемое длительностью импульса, действующего на входе цепи, и параметрами этой цепи. Тем не менее, в импульсной технике принимают следующие допущения, позволяющие упростить анализ электрических цепей с сосредоточенными параметрами. Эти допущения носят название законов коммутации: 1. Токи, протекающие через конденсаторы и резисторы, могут изменяться скачкообразно. 2. Напряжения на индуктивностях и резисторах могут изменяться скачкообразно. Первый закон коммутации можно объяснить следующим образом. Известно, что ток, протекающий через ёмкость, и напряжение на этой ёмкости связаны следующими соотношениями:
и Из выражения (1.11) следует, что при любом конечном изменении тока ic(t), заряжающего конденсатор, напряжение на нём скачком изменяться не может. Аналогично можно объяснить второй закон коммутации. Известно, что напряжение, приложенное к индуктивности, и протекающий через неё ток связаны следующими соотношениями:
и Из выражения (1.13) следует, что при любом конечном изменении напряжения на индуктивности ток через неё скачком изменяться не может. Наличие переходных процессов является причиной искажения формы импульсов, действующих в линейной цепи. Если бы все процессы в цепи устанавливались мгновенно, то никаких искажений импульсов в линейной цепи не было бы.
Задачи и упражнения 1. Амплитуда импульса равна 11 кВ, длительность импульса 1 мкс. Определить крутизну фронта импульса, если считать длительность фронта равной 20 % длительности импульса. 2. Амплитуда прямоугольных импульсов, имеющих частоту следования 1250 Гц и скважность 2300, равна 11 кВ. Определить крутизну фронта и среза, если считать длительность фронта и среза равной 20 % от длительности импульса. 3. Определить постоянную времени цепи, состоящей из конденсатора ёмкостью 5000 пФ и активного сопротивления 0,5 Мом. 4. Определить постоянную времени цепи, состоящей из индуктивности 20 мГн и активного сопротивления 5 кОм. 5. Определить среднюю мощность радиопередающего устройства РЛС, имеющую следующие параметры: импульсная мощность 800 кВт; длительность зондирующего импульса 3,2 мкс; частота следования зондирующих импульсов 375 Гц. 6. Конденсатор ёмкостью 400 пФ заряжается от источника постоянного напряжения 200 В через сопротивление 0,5 Мом. Определить напряжение на конденсаторе через 600 мкс после начала заряда. 7. К цепи, состоящей из конденсатора ёмкостью 10 пФ и сопротивления 2 Мом, подключён источник постоянного тока с напряжением 50 В. Определить ток в момент включения и через 40 мкс после включения. 8. Конденсатор, заряженный до напряжения 300 В, разряжается через сопротивление 300 Мом. Определить величину разрядного тока через время t = 3τ после начала разряда. 9. Какое потребуется время для заряда конденсатора ёмкостью 100 пФ до напряжения 340 В, если напряжение источника 540 В и сопротивление цепи заряда 100 кОм? 10. Цепь, состоящая из индуктивности 10 мГн и сопротивления 5 кОм, подключена к источнику постоянного напряжения 250 В. Определить ток, протекающий в цепи через 4 мкс после включения.
Глава 2. Формирование импульсов
Линейные и нелинейные цепи В импульсной технике широко применяются цепи и устройства, формирующие напряжения одной формы из напряжения другой. Такие задачи решаются с помощью линейных и нелинейных элементов. Элемент, параметры которого (сопротивление, индуктивность, ёмкость) не зависят от величины и направления токов и приложенных напряжений, называется линейным.Цепи, содержащие линейные элементы, называются линейными. Свойства линейных цепей: · Вольт-амперная характеристика (ВАХ) линейной цепи представляет собой прямую линию, т.е. величины токов и напряжений будут связаны между собой линейными уравнениями с постоянными коэффициентами. Пример ВАХ такого вида – закон Ома: · Для расчёта (анализа) и синтеза линейных цепей применим принцип суперпозиций (наложения). Смысл принципа суперпозиций заключается в следующем: если к входу линейной цепи приложено синусоидальное напряжение, то напряжение на любом её элементе будет иметь такую же форму. Если же входное напряжение является сложным сигналом (т.е. является суммой гармоник), то на любом элементе линейной цепи сохраняются все гармонические составляющие этого сигнала: иначе говоря, сохраняется форма приложенного к входу напряжения. При этом на выходе линейной цепи изменится только соотношение амплитуд гармоник. · Линейная цепь не преобразует спектр электрического сигнала. Она может изменить составляющие спектра только по амплитуде и фазе. Это является причиной возникновения линейных искажений. · Всякая реальная линейная цепь искажает форму сигнала за счёт переходных процессов и конечной ширины полосы пропускания. Строго говоря, все элементы электрических цепей нелинейны. Однако в определённом интервале изменения переменных величин нелинейность элементов проявляется настолько мало, что практически можно пренебречь ею. Примером может служить усилитель радиочастоты (УРЧ) радиоприёмника, на вход которого подаётся очень малый по амплитуде сигнал от антенны. Нелинейность входной характеристики транзистора, стоящего в первом каскаде УРЧ, в пределах нескольких микровольт настолько мала, что её просто не учитывают. Обычно область нелинейного поведения элемента ограничена, а переход к нелинейности может происходить либо постепенно, либо скачкообразно. Если на вход линейной цепи подать сложный сигнал, который является суммой гармоник разных частот, а линейная цепь содержит частотно-зависимый элемент (L или C), то форма напряжений на её элементах не будет повторять форму входного напряжения. Это объясняется тем, что гармоники входного напряжения по-разному пропускаются такой цепью. В результате прохождения входного сигнала через ёмкости и индуктивности цепи соотношения между гармоническими составляющими на элементах цепи изменяются по амплитуде и фазе по отношению к входному сигналу. В результате соотношения между амплитудами и фазами гармоник на входе цепи и на её выходе не одинаковы. Это свойство положено в основу формирования импульсов с помощью линейных цепей. Элемент, параметры которого зависят от величины и полярности приложенных напряжений или протекающих токов, называется нелинейным, а цепь, содержащую такие элементы, называют нелинейной. К нелинейным элементам относятся электровакуумные приборы (ЭВП), полупроводниковые приборы (ППП), работающие на нелинейном участке ВАХ, диоды (вакуумные и полупроводниковые), а также трансформаторы с ферромагнетиками.
Свойства нелинейных цепей: · Ток, протекающий через нелинейный элемент, не пропорционален приложенному к нему напряжению, т.е. зависимость между напряжением и током (ВАХ) носит нелинейный характер. Примером такой ВАХ служат входные и выходные характеристики ЭВП и ППП. · Процессы, протекающие в нелинейных цепях, описываются нелинейными уравнениями различного вида, коэффициенты которых зависят от самой функции напряжения (тока) или от её производных, а ВАХ нелинейной цепи имеет вид кривой или ломаной линии. Примером могут служить характеристики диодов, триодов, тиристоров, стабилитронов и др. · Для нелинейных цепей принцип суперпозиций неприменим. При воздействии внешнего сигнала на нелинейные цепи в них всегда возникают токи, содержащие в своём составе новые частотные составляющие, которых не было во входном сигнале. Это является причиной возникновения нелинейных искажений, в результате чего сигнал на выходе нелинейной цепи всегда отличается по форме от входного сигнала.
Дифференцирующие цепи Для того чтобы получить импульс желаемой формы из заданной формы напряжения с помощью пассивной электрической цепи, необходимо знать формирующие свойства этой цепи. Формирующие свойства характеризуют способность линейной цепи определённым образом изменять форму передаваемого (обрабатываемого) сигнала и полностью определяются видом её частотных и временн ы х характеристик. В импульсной технике для формирования сигналов широко применяются линейные двух- и четырёхполюсники. Дифференцирующей называется цепь, на выходе которой напряжение пропорционально первой производной от входного напряжения. Математически это выражается следующей формулой:
где Uвх – напряжение на входе дифференцирующей цепи; Uвых – напряжение на выходе дифференцирующей цепи; k – коэффициент пропорциональности. Дифференцирующие цепи (ДЦ) применяются для дифференцирования видеоимпульсов. При этом дифференцирующие цепи позволяют производить следующие преобразования: · укорочение прямоугольных видеоимпульсов и формирование из них остроконечных импульсов, служащих для запуска и синхронизации различных импульсных устройств; · получение производных по времени от сложных функций. Это используется в измерительной технике, системах авторегулирования и автосопровождения; · формирование прямоугольных импульсов из пилообразных. Простейшими дифференцирующими цепями являются ёмкостная (RC ) и индуктивная (RL ) цепи (рис.2.1):
а) б) Рис.2.1. Виды дифференцирующих цепей: а) ёмкостная ДЦ; б) индуктивная ДЦ
Индуктивная дифференцирующая цепь применяется гораздо реже, чем ёмкостная по чисто практическим соображениям. Дело в том, что для выполнения условия дифференцирования требуется катушка с большой индуктивностью. Такие катушки без железа получаются очень громоздкими и имеют боль-шую паразитную (межвитковую) ёмкость, искажающую результат дифференцирования. Применять же катушки с железом нежелательно, т.к. искажается форма тока из-за нелинейности кривой намагничивания железа, вследствие чего при дифференцировании возникают нелинейные искажения выходного сигнала. Поэтому мы будем рассматривать ёмкостную дифференцирующую цепь. Покажем, что RC - цепь при определённых условиях становится дифференцирующей. Известно, что ток, протекающий через ёмкость, определяется выражением:
В то же время из рис.2.1, а очевидно, что
т.к. R и C представляют собой делитель напряжения. Поскольку напряжение
Выходное напряжение
Подставив выражение (2.2) в (2.3), получим:
Если выбрать достаточно малую величину R так, чтобы выполнялось условие, то получим приближённое равенство
Это равенство тождественно (2.1). Выбрать R достаточно малой величины – это значит обеспечить выполнение неравенства
где ωв = 2πfв – верхняя граничная частота гармоники выходного сигнала, ещё имеющая существенное значение для формы выходного импульса. Коэффициент пропорциональности в выражении (2.1) k = RC = τ носит название постоянной времени дифференцирующей цепи. Чем резче изменяется подводимое напряжение, тем меньшей величиной τ должна обладать дифференцирующая цепь, чтобы на выходе напряжение было близко по форме к производной от Uвх. Параметр τ = RC имеет размерность времени. Это можно подтвердить тем, что в соответствии с Международной системой единиц (СИ) единица измерения электрического сопротивления
а единица измерения электрической ёмкости
Следовательно,
Принцип действия дифференцирующей цепи. Принципиальная схема ёмкостной дифференцирующей цепи изображена на рис.2.2, а эпюры напряжений – на рис.2.3.
Рис.2.2. Принципиальная схема ёмкостной дифференцирующей цепи
Пусть на вход подаётся идеальный прямоугольный импульс, у которого τф= τс = 0, а внутреннее сопротивление источника сигнала Ri = 0. Пусть импульс определяется следующим выражением:
В исходном состоянии Uвх = 0; Uс = 0; iс = 0; Uвых = 0.
В момент времени t = t1 на вход ДЦ подаётся скачком напряжение Uвх = Е. В этот момент Uс = 0, т.к. за бесконечно малый промежуток времени ёмкость зарядиться не может. Но, в соответствии с законом коммутации, ток через ёмкость может нарастать мгновенно. Следовательно, в момент t = t1 ток, протекающий через ёмкость, будет равен Поэтому напряжение на выходе цепи в этот момент будет равно
После скачка начинается заряд конденсатора током, убывающим по экспоненциальному закону:
Рис.2.3. Эпюры напряжений на элементах дифференцирующей цепи
Напряжение на конденсаторе будет нарастать по экспоненциальному закону:
Напряжение на выходе ДЦ будет падать по мере нарастания напряжения заряда на конденсаторе, т.к. R и C представляют собой делитель напряжения:
Необходимо помнить, что в любой момент времени для делителя напряжения выполняется равенство
откуда следует, что
что подтверждает справедливость выражения (2.7). Теоретически заряд конденсатора будет продолжаться бесконечное время, но практически этот переходный процесс заканчивается через (3…5) τзар = (3…5) RC.
После окончания переходного процесса ток заряда конденсатора стано-вится равным нулю. Поэтому напряжение на выходе дифференцирующей цепи
достигает практически нулевого значения, т.е. в момент времени t = t2
При этом
В момент времени t = t3 напряжение на входе дифференцирующей цепи скачком падает до нуля. Конденсатор C становится источником напряжения, т.к. он заряжен до величины Так как в соответствии с законом коммутации напряжение на конденсаторе скачком изменяться не может, а ток, протекающий через ёмкость, может изменяться скачкообразно, то в момент t = t3 напряжение на выходе скачком уменьшается до – Е. При этом ток разряда в данный момент времени становится максимальным:
а напряжение на выходе дифференцирующей цепи
Выходное напряжение имеет знак «минус», т.к. ток изменил своё направление.
После второго скачка напряжение на конденсаторе начинает уменьшаться по экспоненциальному закону:
После окончания переходного процесса разряда конденсатора
Таким образом, схема возвратилась в исходное состояние. Окончание разряда конденсатора наступает практически при t = (3…5)τ = (3…5) RC. Так как мы приняли внутреннее сопротивление источника сигнала Ri = 0, то можно считать, что постоянные времени цепей заряда и разряда конденсатора τзар = τраз = τ = RC. В такой идеальной цепи амплитуда выходного напряжения Uвых.mах не зависит от значения параметров цепи R и C, а длительность импульсов на выходе определяется величиной постоянной времени цепи τ = RC. Чем меньше значения R и C, тем быстрее заканчиваются переходные процессы заряда и разряда ёмкости, тем короче импульс на выходе цепи. Теоретически длительность импульса на выходе дифференцирующей цепи, определяемая по основанию, оказывается бесконечно большой, поскольку напряжение на выходе спадает экспоненциально. Поэтому длительность импульса определяется на определённом уровне от основания U0 = αUвых (рис.2.4):
Рис.2.4. Определение длительности импульса на уровне U0 после дифференцирования
Определим длительность продифференцированного импульса на уровне U0 = αUвых:
откуда Дифференцирование всегда сопровождается укорочением длительности импульса. Это означает, что ёмкость C должна успевать полностью зарядиться за время действующего входного дифференцируемого импульса. Следовательно, условием практического дифференцирования с целью укорочения длительности импульса является соотношение: τи вх > 5τ = 5RC. Чем меньше τ цепи, тем быстрее заряжается и разряжается конденсатор и тем меньшую длительность имеют выходные импульсы, тем более остроконечными они становятся и, следовательно, тем точнее дифференцирование. Однако уменьшать τ целесообразно до определённого предела. Изменение формы импульса на выходе дифференцирующей цепи можно объяснить с точки зрения спектрального анализа. Каждая гармоника входного импульса делится между R и C. Для гармоник низких частот, определяющих вершину входного импульса, конденсатор представляет большое сопротивление, т.к.
Поэтому на выход плоская вершина входного импульса почти не передаётся. Для высокочастотных составляющих входного импульса, формирующих его фронт и срез,
Поэтому фронт и срез входного импульса на выход передаются практически без ослабления. Эти соображения позволяют определить дифференцирующую цепь как фильтр верхних частот.
Переходные цепи В многокаскадных усилителях (в том числе и импульсных) напряжение с выхода предыдущего каскада на вход следующего передаётся, как правило, через переходные RC - цепи. Такие цепи должны обеспечивать выполнение двух условий: · минимальные искажения входного сигнала; · разделение («развязка») каскадов по постоянной составляющей. Последнее условие необходимо выполнять, потому что режим работы по постоянному току последующего каскада усиления должен выбираться независимо от постоянной составляющей выходного напряжения предыдущего каскада. Схема переходной цепи по начертанию ничем не отличается от дифференцирующей цепи (рис.2.2). Однако если в дифференцирующей цепи обязательно выполнение соотношения τ << τи, то в переходной цепи это соотношение должно быть τ >> τи. Принцип действия переходной цепи. Будем считать, что на вход переходной цепи подаётся идеальный прямоугольный импульс, у которого τф = τс = 0 и амплитуда входного напряжения Uвх = Е. Принцип действия и эпюры напряжений на элементах переходной цепи показаны на рис.2.7. 1. Исходное состояние схемы (t < t1). В исходном состоянии Uвх = 0; UС = 0; UR = Uвых = 0. 2. Первый скачок напряжения (t = t1). В момент t = t1 происходит скачок напряжения на входе переходной цепи. За время действия фронта импульса в соответствии с законом коммутации конденсатор C мгновенно зарядиться не может, поэтому UС = 0 и UR = Е. 3. Заряд конденсатора (t1 < t < t2). С момента времени t = t1 напряжение на конденсаторе начинает увеличиваться по экспоненциальному закону
а ток, протекающий через ёмкость, убывает также по экспоненциальному закону
Поскольку постоянная времени переходной цепи τ >> τи, то заряд конденсатора будет происходить медленно. Так же медленно спадает по экспоненте напряжение на выходе. Заряд ёмкости происходит до момента времени t2 = τи. 4. Второй скачок напряжения (t = t2). В этот момент на входе импульс скачком падает до нуля. В соответствии с законом коммутации напряжение на конденсаторе мгновенно измениться не может, но скачкообразно пропадает ток, протекающий через конденсатор. Это вызывает отрицательный скачок напряжения на выходе схемы.
Рис.2.7. Эпюры напряжений на элементах переходной цепи
5. Разряд конденсатора и восстановление исходного состояния схемы (t > t2). После отрицательного скачка напряжения начинается разряд конденсатора, который происходит по экспоненциальному закону. Чем больше постоянная времени переходной цепи, тем дольше будет длиться разряд конденсатора. Таким образом, одиночный импульс через переходную цепь проходит с искажениями тем меньшими, чем больше постоянная времени этой цепи. Искажения сигнала при прохождении его через линейную переходную цепь принципиально неизбежны. Эти искажения заключаются в том, что вершина прямоугольного импульса при его передаче уменьшается на величину ΔUвых, а после окончания входного импульса на выходе цепи появляется экспоненциальный хвост противоположной полярности. Для уменьшения искажений ёмкость C за время действия входного импульса не должна заметно заряжаться, чтобы спад напряжения на выходе цепи был незначительным. Следовательно, чтобы искажения сигнала на выходе переходной цепи были минимальными, необходимо выполнить условие τ = RC >> (5 …10) τи, что соответствует неравенству
Интегрирующие цепи Интегрирующей называется цепь, величина выходного напряжения которой пропорциональна интегралу по времени от величины входного напряжения.Математически это выражается следующей формулой: Интегрирующие цепи (ИЦ) могут быть двух видов: ёмкостные (RC) и индуктивные (RL). Схемы этих цепей показаны на рис.2.8. В радиоэлектронике чаще всего применяются ёмкостные интегрирующие цепи. Интегрирующие цепи применяются в качестве сглаживающих фильтров блоков питания и в формирующих устройствах, где вырабатываются пилообразные или трапецеидальные напряжения. Покажем, что при определённых условиях RC - цепь, изображённая на рис.2.8, становится интегрирующей.
а) ёмкостная б) индуктивная Рис.2.8. Виды интегрирующих цепей: Известно, что напряжение на конденсаторе и ток, протекающий через него, связаны интегральной зависимостью:
Для простоты рассуждений будем считать, что начальный заряд конденсатора равен нулю. Интегрирующая цепь представляет собой делитель напряжения, ток через который равен:
Подставив это выражение в (2.11), получим:
Если выбрать R >> xc для высшей гармоники ωв прямоугольного импульса,
Тогда последнее выражение примет вид:
Выражение (2.13) показывает, что чем точнее выполняется неравенство
Принцип действия интегрирующей цепи Пусть на вход схемы воздействует идеальный прямоугольный импульс (т.е. τф = τс = 0). Паразитные параметры схемы учитывать не будем. Внутреннее сопротивление источника сигнала Ri добавляется к достаточно большому сопротивлению цепи R, и его также учитывать не будем. Эпюры напряжений на элементах интегрирующей цепи показаны на рис.2.9. 1. Исходное состояние схемы (t < t1).
2. Первый скачок (t = t1). В этот момент на вход интегрирующей цепи подаётся прямоугольный импульс с амплитудой Uвх = Е. В соответствии с законом коммутации в момент t = t1 напряжениена конденсаторескачком измениться не может. Ток через конденсатор увеличивается скачком, и всё входное напряжение падает на сопротивлении (так как при τф = 0
Рис.2.9. Эпюры напряжений на элементах интегрирующей цепи
3. Заряд ёмкости (t1 < t < t2). После скачка начинается заряд ёмкости током, спадающим по экспоненте:
Напряжение на ёмкости нарастает по экспоненциальному закону:
4. Разряд ёмкости и восстановление исходного состояния схемы (t > t2). В момент t = t2 импульс на входе прекращается, и конденсатор, заряженный до величины UС m, начинает разряжаться. Отрицательный скачок тока в этот момент создаёт на сопротивлении R максимальное падение напряжения Um = – Е. С этого момента конденсатор начинает разряжаться по экспоненциальному закону:
Окончание разряда наступает через (3…5) τ. Таким образом, интегрирующая цепь вида RC на выходе даёт экспоненциально изменяющееся напряжение фронта и среза выходных импульсов. Ошибка интегрирования зависит от параметров цепи. Чем больше величина τ=RC, тем меньше отклонение выходного напряжения от линейного закона, тем точнее интегрирование входного напряжения, но тем меньше амплитуда напряжения
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 1621; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.053 с.) |




 …………………………...... (1.10)
…………………………...... (1.10) ……………………(1.11).
……………………(1.11). ………………………….... (1.12)
………………………….... (1.12) ……………….... (1.13).
……………….... (1.13).
 .
. ………………………. (2.1),
………………………. (2.1),

 ........................................... (2.2).
........................................... (2.2). ,
, , то
, то  .
. ………………….... (2.3).
………………….... (2.3). ……………… (2.4).
……………… (2.4).
 ……………………….. (2.5).
……………………….. (2.5). , т.е.
, т.е.  ,
,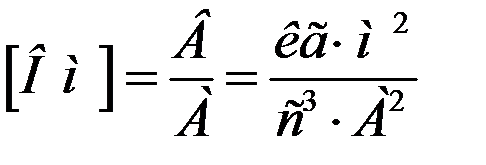 ,
, .
.






 …………………… (2.6).
…………………… (2.6). …………. (2.7).
…………. (2.7).
 ,
,








 .
. ,
, .
. ;
;  ;
; 





 ………………. (2.8),
………………. (2.8), и
и  ……………………… (2.9).
……………………… (2.9).
 >> R.
>> R. << R.
<< R. ,
,


 …………………….. (2.10).
…………………….. (2.10). 

 …………………. (2.11).
…………………. (2.11). ………………………… (2.12).
………………………… (2.12). .
. , то
, то  и, следовательно,
и, следовательно,  .
. ……………… (2.13).
……………… (2.13).

 ).
).
 .
.
 .
.


