
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структурирование при цифровом моделировании.Содержание книги
Поиск на нашем сайте
Как уже отмечалось, для успешного моделирования (особенно сложных систем) желательно в той или иной мере структурировать объект. Для этого объект разбивается на блоки. Разумеется, можно использовать традиционный путь: используя структурную схему системы регулирования, свернуть её по правилам теории автоматического регулирования (ТАУ), получить общую передаточную функцию, а затем получить общее уравнение. Однако это не будет наглядной моделью отражающей физическую реальность. Для сравнения выберем два варианта составления дифференциальных уравнений: по отдельным звеньям и по связи их в общую цифровую модель.
В качестве примера возьмём систему второго порядка состоящую из двух апериодических звеньев, которая можнт быть представлена в свёрнутом (рис. 37) и развёрнутом (рис. 38) виде.
Рис. 55 Система регулирования в свёрнутом виде.
Рис. 56 Система регулирования в развёрнутом виде.
I. Выведем передаточную функцию системы представленной на рисунке 37:
или
Известно, что уравнение высшего порядка может быть сведено к системе уравнений первого порядка. Переход во временную область:
Введём вспомогательную переменную:
с учётом вспомогательной переменной перепишем уравнение (81)
Таким образом, записав передаточную функцию и выполнив подстановку вспомогательной переменной, получим систему дифференциальных уравнений описывающих свернутую систему второго порядка:
Аналогично можно составить систему уравнений для более высоких порядков. Необходимо отметить, что замена переменной справедлива в том случае, если в числителе передаточной функции нет оператора II. Запишем систему уравнений для развёрнутой системы представленной на рисунке 38.
Используя передаточные функции (см. (85)) выведем математическое описание в операторной форме:
Переход во временную область для представления математического описания в форме дифференциальных уравнений:
Математические описания (84) и (87) по форме эквивалентны. Для доказательства эквивалентности необходимо ввести в систему (87) промежуточную переменную Составление уравнений по звеньям имеет преимущество, т.к. не требуется вводить вспомогательные переменные; и составление уравнений по звеньям имеет наглядность физических процессов протекающих в отдельных структурах.
Выбор вспомогательных переменных для передаточных функций, содержащих оператор
Оператор
или
Во временной области:
В принципе это уравнение применять нежелательно, т.к. в правой части содержится производная входного сигнала, которую необходимо вычислять численным методом, либо нужна функциональная зависимость входного сигнала от времени и тогда производную можно задать аналитически. К тому же такое уравнение обычными заменами переменных не сможем привести к форме Коши. Уравнение (89) разделим на оператор
Введём замену переменных:
или
Выполнив замену переменных и осуществив переход во временную область, получим математическое описание форсирующего звена состоящую из двух дифференциальных и одного алгебраического уравнений:
По функциям Как уже отмечалось, выбор промежуточных переменных позволяет получить различную форму записи дифференциальных уравнений. Например, в методе переменных состояний используется следующий подход для вывода дифференциальных уравнений. Используем передаточную функцию (88), преобразуем её:
Введём вспомогательную функцию:
Следовательно,
и
введём дополнительную вспомогательную переменную
Выразим Е через х (см. выражение 100):
Окончательно система запишется в виде:
Гибридное моделирование
Преимущества аналогового и цифрового моделирования могут быть объединены принципом аналого-цифровым моделированием (или как его еще называют - гибридным). Суть данного вида моделирования заключается в том, что уравнения описывающие объект решаются аналоговым способом, а коэффициенты - цифровым моделированием. Области применения гибридного моделирования: 1) Там, где с вместе с высоким быстродействием предъявляются высокие требования к точности; 2) Там, где требуется автоматизация получения результатов; 3) Тенденция перехода к гибридному моделированию связанно с широким применением вычислительных машин в контурах регулирования.
Система MATLAB
Поскольку в настоящее время имеется большое количество пакетов программного обеспечения для решения задач связанных с математическими вычислениями и моделированием разнообразных динамических систем, рассмотрим более подробно один из них, а именно систему высокопроизводительных численных вычислений и визуального представления результатов Matlab, в которую входят программные средства моделирования динамических систем Simulink.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.147.193 (0.006 с.) |



 (79)
(79) (80)
(80) (81)
(81) (82)
(82) (83)
(83) (84)
(84) , его наличие вызывает осложнение при выводе общего уравнения.
, его наличие вызывает осложнение при выводе общего уравнения. (85)
(85) (86)
(86) (87)
(87) . После соответствующих преобразований система (87) будет полностью эквивалентна системе уравнений (84).
. После соответствующих преобразований система (87) будет полностью эквивалентна системе уравнений (84). в числителе
в числителе содержится в числителе таких передаточных функций, как форсирующие звенья. Передаточная функция форсирующего звена:
содержится в числителе таких передаточных функций, как форсирующие звенья. Передаточная функция форсирующего звена: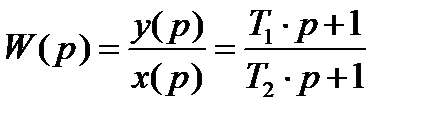 (88)
(88) (89)
(89)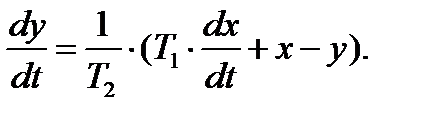 (90)
(90) (91)
(91) (92)
(92) (93)
(93) (94)
(94) (95)
(95) (96)
(96) и
и  находят искомую функцию
находят искомую функцию  .
. (97)
(97) (98)
(98) (99)
(99)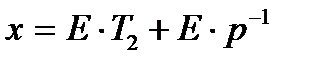 (100)
(100) , получим:
, получим: (101)
(101) (102)
(102) (103)
(103)


