
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Идентификация динамических систем
Допустим, динамическая система описана передаточной функцией следующего вида:
1. Получаем систему дифференциальных уравнений первого порядка из n - уравнений
где Y – выходные переменные, U(t) – входные переменные, Х – внутренние переменные. Как получить эту систему? I. а) б) в) Замена переменной г) получаем систему n – го порядка дифференциальных уравнений первого порядка. II. C помощью методов пространства состояния. 2. От дифференциальных уравнений переходим к разностным уравнениям
где 3. получаем матрицу перехода:
при этом V(к) при е измерений примет значение:
Если
Количество измерений определяется по аналогичной формуле для линейного регрессионного анализа.
Идентификация нелинейных систем Существует несколько методов идентификации нелинейных систем: 1. Метод прямого поиска; 2. Аппроксимация нелинейности; 3. Модель Гаммерштейна; 4. Метод Виннера; 5. Двухэтапная процедура.
Метод прямого поиска Нелинейную функцию f(x) преобразуют в линейную функцию fл(x). Далее применяют любой метод идентификации линейных систем. Допустим, что модель объекта имеет вид:
где х1, х2 – входные параметры, у – выходной параметр, а0, в1, в2 – искомые параметры.
Рассматриваем только положительные значения у.
Аппроксимация нелинейности Таблично заданная функция (явно нелинейная) аппроксимируется с помощью полинома произвольным методом. Полученный полином и есть модель нашего объекта. Ограничения: функция должна быть непрерывна. Существует теорема Вейерштрасса, которая доказывает, что все нелинейности можно описать полиномом:
а) Замена линейной переменной и сведение к регрессии; б) Применение интегральных формул.
Модель Гаммерштейна Входной сигнал u(t) известен. 1. Если известна функциональная зависимость f(u(t)) – вид нелинейности, то вводим Z=f(u(t)). Идентификация сводится к определению параметров линейной части:
2. Функциональная зависимость f(u(t)) не известна. Строится таблица этой нелинейной зависимости. По этой таблице любой интерпретируемой формулой получаем аппроксимирующий полином нелинейности f*(u(t)). Зная параметры аппроксимирующего полинома, вводим Z(t) =f*(u(t)) и, снимая соответствующие ему y(t), решаем задачу идентификации:
Пример: Система приводится к следующему виду:
Рис. 22 Схема нелинейной системы
Используя метод интерполяции, аппроксимируем полином
Составляем обобщенный вектор:
Тогда искомая матрица:
может быть получена по выражению:
где
Метод Виннера Является наиболее точным методом идентификации, на практике применяется крайне редко из-за сложности вычислений и отсутствия ясной физической интерпретации.
Двухэтапная процедура 1. Нелинейная характеристика разбивается на участки, в пределах которых нелинейная функция может быть с достаточной долей точности представлена линейной функцией. Данные участки называются участками линеаризации. Начало участков называется точкой линеаризации. В каждой точке линеаризации входной переменной придается незначительное приращение и фиксируется изменение выходной переменной. По данным входного и выходного переходного процесса с помощью линейных методов идентификации строятся линейные модели. 2. Аппроксимация линейных моделей в нелинейную функцию. На основе зарегистрированного переходного процесса строится матрица коэффициентов линейным реверсионным методом. В результате получим столько матриц, сколько узловых точек. Каждый коэффициент матрицы аппроксимируется по той или иной интерполяционной формуле с помощью любого полинома. Пример: Рассматривается отдельно нелинейное звено. На нелинейной характеристике выбирается отрезок, где система ведет себя как линейная функция.
Рис. 23 График нелинейной функции
Отрезок, где функция линейна - Для точек линеаризации подбираем соответствующие входные точки
Каждой точке линеаризации подаем входную переменную, увеличивающуюся на величину
Снимаем переходный процесс системы для каждой точки линеаризации. Для каждой точки линеаризации получаем линейную модель Аi
По каждому aij получаем функциональную зависимость aij = f(aij) методом аппроксимации тем же самым полиномом
Планирование эксперимента Пассивным экспериментом называют эксперимент, в котором регистрация входных и выходных данных осуществляется в рабочем режиме, не используя дополнительных вмешательств. Он применяется тогда, когда структура модели хорошо известна и ее адекватность не вызывает сомнений (когда решаются задачи параметрической идентификации). Активный эксперимент предполагает особую программу проведения наблюдений таких, что позволяют по результатам исследований дополнительно оценить структуру модели.
Активный эксперимент Факторами активного эксперимента называют переменные, по которым возможно проводить управление и которые участвуют в построении модели (хi). Каждый из факторов может принимать различные значения, которые называются уровнями. На практике, количество уровней – это бесконечное количество или непрерывный ряд уровней
Фиксированный набор уровней называется состоянием факторов. План – это программа проведения эксперимента, позволяющая использовать все факторы на всех уровнях. Если план содержит всевозможные сочетания факторов и уровней, то такой план называют полным. Если р – общее количество уровней; к – количество факторов, то полный план эксперимента будет включать в себя следующее количество экспериментов:
Пример: к = 3, р = 4, то N = 43 = 64 - эксперимента. Полный план позволяет построить адекватную модель, но требует большого количества экспериментов. Поэтому на практике применяют усеченные планы, так называемые дробные планы, которые имеют количество экспериментов меньше, чем полный план, но с достаточной долей точности могут определить адекватность модели. Любая модель определяется по формуле:
где [XXT]-1 = M – называется информационной матрицей. 1. Если информационная матрица ставится по принципу минимизации определителя, то выбранный план эксперимента будет называться D – планом.
2. Если минимизируется след матрицы, то такой план называется А – планом.
3. Условием задания Е – плана является выбор плана таким, чтобы максимальное собственное число матрицы М было минимальным.
На практике чаще строятся D – планы.
Построение D – плана
Основным условием D – плана является то, что план будет отвечать условию оптимальности, если информационная матрица М будет диагональной. Пример: р = 2, к = 3, Соответственно, полный план будет иметь вид: 23 = 8
Тогда, с учетом этого условия, выбирается некий дробный план: 23-1 = 4
т.е. откидываем любую переменную (x3) и план уменьшается на 4 единицы. Для оставшихся двух переменных строится полный план, а x3 считается равной
Построенный по такому принципу D – план отвечает условиям D – оптимальности, при этом переменная x3 называется генератором дробного плана. Для двухуровневой систем количество экспериментов равно 2к-N, где N<к, а оставшиеся генераторы плана составляются следующим образом: как результаты поэлементного умножения основных факторов, при этом количество множителей составляет от 2 до N-к.
Пример: 26-4
Выбор двух уровней из непрерывного ряда уровней:
-1 – начало уровней x0i; +1 – конец уровней xni.
Оценка адекватности модели Оценка адекватности модели определяется статистическими методами по следующему алгоритму: 1. Выбор структуры модели А, определение ее порядка к. 2. Ставится N экспериментов по какому – либо плану и определяется параметр модели А. 3. Этот план экспериментов повторяется l раз. 4. По результатам определяем 5. Определяем 6. Определяем полную сумму квадратов по следующему признаку 7. Определяется коэффициент 8. Определяется критерий 9. Выбирается Fкр по таблице Фишера. 10. Проверяется, если
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 292; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.150.55 (0.03 с.) |
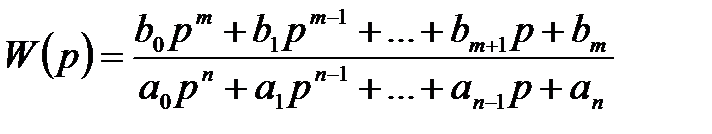
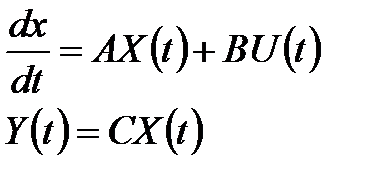


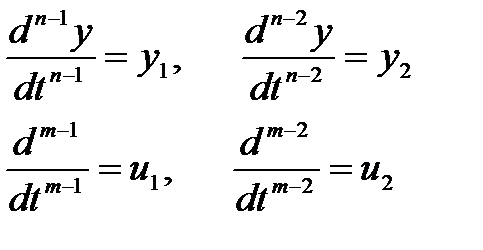

 - обобщенный вектор.
- обобщенный вектор. ,
,
 , то при
, то при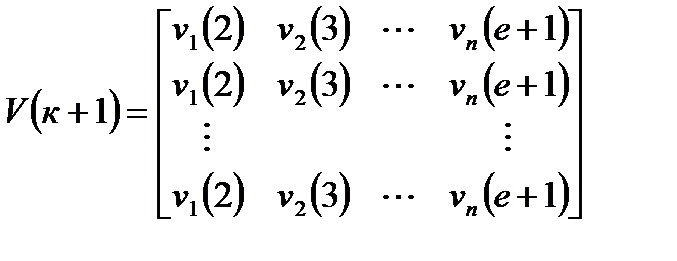
 ,
,

 .
. .
.
 - функция является нелинейной.
- функция является нелинейной.


 ,
,

 , где x1i – точки или узлы линеаризации.
, где x1i – точки или узлы линеаризации. .
.
 .
.
 .
. . В теории активного эксперимента этот ряд дискретизируется, и выбираются отдельные уровни:
. В теории активного эксперимента этот ряд дискретизируется, и выбираются отдельные уровни:
 .
. ,
,



 .
.
 .
. , где
, где  .
. и степень свободы
и степень свободы  .
. где
где  .
. .
. , то модель адекватна; если
, то модель адекватна; если  , то модель неадекватна.
, то модель неадекватна.


