
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрально-пропорциональный усилительСодержание книги
Поиск на нашем сайте
Интегрально-пропорциональный усилитель в технической литературе встречается как апериодическое или инерционное звено. Принципиальная схема:
Рис. 35 Апериодическое звено.
Передаточная функция интегрально-пропорционального звена:
где
Отношение
Схема набора:
Рис. 36 Условное представление апериодического звена.
Где
Дифференциальное звено
Принципиальная схема дифференциального звена:
Рис. 37 Дифференциальный усилитель.
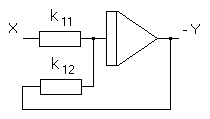
Данное звено позволяет производить операцию дифференцирования (нахождение производной). Передаточная функция звена:
где произведение
Постоянная времени Т в практических схемах имеет большое значение, то это приводит к ошибкам при дифференцировании быстро изменяющихся величин. С другой стороны Т влияет на точность решения, т.е. чем она больше, тем выше точность и наоборот. Поэтому на практике представленное выше дифференциальное звено не применяют. Однако схему дифференцирования можно получить со схемы интегрирования. Докажем это. Пусть мы имеем дифференциальное уравнение I-го порядка:
Преобразуем данное уравнение:
Таким образом, преобразуя исходное дифференциальное уравнение процесс нахождения производной можно выполнить схемой интегрально-пропорционального звена. Схема набора:
Рис. 38 Условное представление звена выполняющего операцию дифференцирование.
Где
Пример аналогового моделирования двигателя постоянного тока
Пусть имеем двигатель постоянного тока (ДПТ) независимого возбуждения, скорость которого регулируется изменением напряжения на якоре. Исходные данные для аналогового моделирования: 1. Уравнение описывающее якорную цепь ДПТ:
где Е=сеФ w - ЭДС наводимая в обмотке якоря при его вращении.
2. Уравнение движения:
где М=смФJя - электромагнитный момент двигателя; Мс - момент сопротивления (нагрузки); J - суммарный момент инерции.
Так как выражения М-Мс и I-Ic тождественно равны, то уравнение движения можно переписать в следующем виде:
Умножим и разделим выражение (37) на смФ и Rя:
где выражение Уравнение движения с учётом введённых поправок:
Переходим к операторной форме записи, заменяя дифференциал Уравнение якорной цепи:
Уравнение движения:
Преобразуем форму записи уравнений (40) и (41) с тем, чтобы получить передаточные функции якорной цепи и механического звена:
Так как выражение · Для якорной цепи:
· Для механической части:
На основании полученных передаточных функций построим структурную схему двигателя постоянного тока независимого возбуждения (ДПТ НВ).
Рис. 39 Структурная сема ДПТ НВ.
По структурной схеме из операционных блоков собирают аналоговую модель ДПТ НВ. Этапы создания аналоговой модели. 1. Масштабирование параметров Iя, w, t, Uя:
где
где
где
где
2. Преобразование уравнений (40) и (41) в удобную форму для моделирования на АВМ:
3. Переход к уравнениям с маштабами:
Производим упрощения в формулах (52), (53) и окончательно получают уравнения используемые в аналоговом моделировании.
4. Составляем схему набора АВМ:
Рис. 40 Схема набора на АВМ модели ДПТ НВ.
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.140 (0.006 с.) |


 (30)
(30) параллельное соединение активного и реактивного (ёмкостного) сопротивлений.
параллельное соединение активного и реактивного (ёмкостного) сопротивлений. есть коэффициент передачи k, а произведение
есть коэффициент передачи k, а произведение  - постоянная времени Т апериодического звена.
- постоянная времени Т апериодического звена.
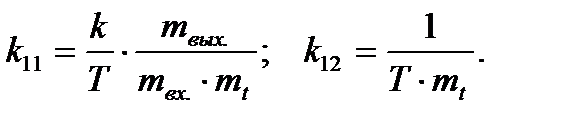

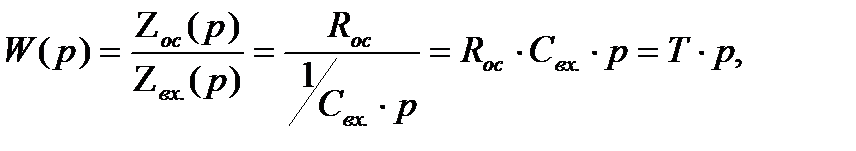 (31)
(31) - это постоянная времени дифференцирования T.
- это постоянная времени дифференцирования T. (32)
(32) (33)
(33) (34)
(34)

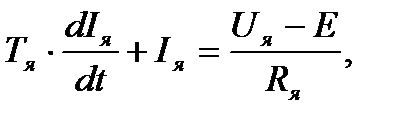 (35)
(35) - постоянная времени якоря;
- постоянная времени якоря; (36)
(36) (37)
(37) (38)
(38) - механическая постоянная времени.
- механическая постоянная времени. (39)
(39) на оператор Лапласа.
на оператор Лапласа. (40)
(40) (41)
(41) (42)
(42) (43)
(43) - входное воздействие на якорную цепь (аналогично для механического звена
- входное воздействие на якорную цепь (аналогично для механического звена 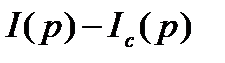 ), а
), а  (
( ) – выходные координаты, то передаточные функции звеньев запишутся так:
) – выходные координаты, то передаточные функции звеньев запишутся так: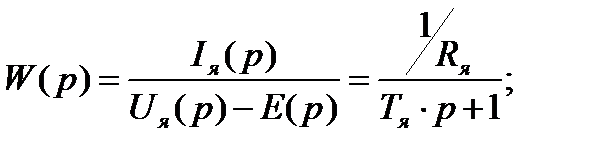 (44)
(44) (45)
(45)
 (46)
(46) - масштаб тока якоря;
- масштаб тока якоря;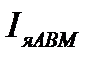 - значение тока якоря используемое в АВМ;
- значение тока якоря используемое в АВМ; - истинное значение физической величины.
- истинное значение физической величины. (47)
(47)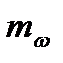 - масштаб угловой скорости вращения якоря;
- масштаб угловой скорости вращения якоря; - значение угловой скорости используемое в АВМ;
- значение угловой скорости используемое в АВМ; - истинное значение скорости вращения якоря.
- истинное значение скорости вращения якоря.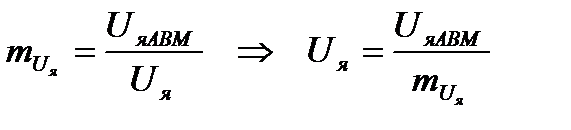 (48)
(48) - масштаб напряжения на якоре;
- масштаб напряжения на якоре; - значение напряжения на якоре используемое в АВМ;
- значение напряжения на якоре используемое в АВМ; - истинное значение физической величины.
- истинное значение физической величины. (49)
(49) - масштаб времени моделирования;
- масштаб времени моделирования; - значение времени моделирования используемое в АВМ;
- значение времени моделирования используемое в АВМ; - истинное значение физической величины.
- истинное значение физической величины. (50)
(50) (51)
(51) (52)
(52) (53)
(53) (54)
(54) (55)
(55)



