
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение критериев подобия при известномСодержание книги
Поиск на нашем сайте
математическом описании Пусть объект описывается уравнением (уравнение – размерная величина).
Любую размерную величину можно представить в виде произведения степенного комплекса размерной величины и безразмерной функции этих же величин. Ф(p1p2…pn) = 0 Из свойств степенных комплексов безразмерная функция размерных величин может быть представлена в виде функции безразмерных степенных комплексов: Ф(p1p2…pn) = j(p1p2…pn), где j(p1p2…pn) = 0 критериальное уравнение. Если математическое описание группы заведомо подобных процессов известно и выглядит, например, как линейное дифференциальное уравнение,
решение которого (общий интеграл имеет вид):
Для конкретного процесса uc(t) изменения напряжения uc во времени t на конденсаторе С в последовательной цепи из конденсатора и активного сопротивления R, которая включается на постоянное напряжение Е, при нулевых начальных условиях. При различных значениях R, C, и Е процессы uc(t) заведомо будут иметь качественно одинаковый характер, что позволяет рассматривать их как группу подобных процессов. Переходный процесс описывается линейным дифференциальным уравнением:
Решение которого имеет вид:
Согласно правилу Фурье все члены уравнения, описывающего какой - либо физический процесс, имеют одинаковую размерность. Поэтому уравнение можно привести к безразмерному виду, если разделить его на один из членов, здесь uc:
если обозначить
Для подобных процессов соотношения пропорциональности справедливы и для «точечных» значений и для малых отклонений от этих параметров D: mu = u1c / u2c = Du1c / Du2c; mt = t1 / t2 = Dt1 / Dt2 (3.4a). С учетом (3.4a) можно записать p1’ и p2’ в виде:
Выражения для p1 и p2, имеющие вид безразмерных степенных комплексов параметров, характеризующих рассматриваемый процесс, называются критериями подобия; критерии подобия численно одинаковы для сходственных точек подобных процессов. Аналогично приводится к безразмерному виду (3.1) путем деления на первый член:
Преобразования аналогичные (3.5а), с учетом (3.4а) позволяют получить для (3.3) систему критериев подобия вида:
P1,..., Pm - параметры рассматриваемого процесса, (Pi = x); cj, aj,..., w j - безразмерные числа, принимающие некоторые действительные, в том числе нулевые, значения. Критерии подобия имеют вид безразмерных степенных комплексов параметров, которые характеризуют процесс.
Пример: Пусть процесс, происходящий в цепи представленной на рис.11 описывается уравнением: Рис. 11 График процесса, происходящего в цепи 1 Тогда параметры, описывающие систему L, c, R, ω, i, u, t, С точки зрения подобия (для вывода критерия подобия)
Замена
Способ интегральных оценок - способ определения критериев подобия по известному математическому описанию процесса путем приведения его к безразмерному виду, при котором символы дифференцирования и интегрирования в выражениях для определения критериев подобия опускаются. Вообще, существует две системы критериев подобия: первая - получаемая из дифференциального уравнения, вторая - из решения (общего интеграла) дифференциального уравнения. Однако обе системы критериев подобия идентичны, т.к. имеют одинаковый физический смысл. Таким образом, интеграл дифференциального уравнения можно представить в виде функции критериев подобия, но при этом констатируется только факт возможности получения такой зависимости, вид связей критериев не устанавливается. Следовательно, в описании системы Для определения количества критериев запишем размерность каждого параметра через основные единицы измерения L, M, T, I:
откидываем как независимую строку (т.к. ранг матрицы определяется количеством независимых параметров).
Откидываем как зависимые строки: (6) [(4)-(3) = (6)], [(2)-(1).3+(3)=(4)], а также 2-ой столбец, тогда максимальный возможный ранг матрицы = 3. Так как определитель матрицы ≠ 0, тогда ранг матрицы 3, соответственно количество независимых параметров k = 3, тогда количество критериев m = (n-k) = (7-3) = 4. Исходное уравнение перепишем с учетом способа интегральных оценок:
где каждое из слагаемых имеет одинаковую размерность. Поделим уравнение на 2-ое слагаемое, получим:
тогда критерии имеют вид:
Критериальное уравнение:
Определение критериев подобия с использованием теории размерности (при неизвестном математическом описании) 1 шаг: Выявление параметров Рi, характеризующих процесс, 2 шаг: Составление полной матрицы размерности параметров Рi (матрица А). 3 шаг: Определение количества зависимых и независимых параметров (k, m = n-k). 4 шаг: Любой зависимый параметр может быть представлен как 2 Если неизвестны математические описания процессов, критерии также можно получить. Для этого функциональную зависимость, полученную из эксперимента или расчета и имеющую в размерных физических величинах P1,..., Pj,..., Pm вид: F(P1,..., Pj,..., Pm) = 0 Или, для рассмотренного примера F(uc, t, R, C, E) = 0 можно представить как Fp(p1, p2,..., pm-k) или Fp(p1 = RC/t, p2, = E/uc) = 0, где p1, p2,..., pm- k - критерии подобия. Для определения критериев подобия в данном случае применяется метод анализа размерностей физических величин Pj, определяющих характер процесса. Возможность установления критериев подобия, когда вид функциональной зависимости неизвестен, создает предпосылки для представления данных экспериментального исследования в обобщенной форме и распространения результатов единичного эксперимента на группу или класс подобных процессов. Допустим, что в качестве основных единиц измерения выбраны [a b …q], тогда размерность 1-го параметра 2-го параметра
n-го параметра Рассмотрим уравнение 2 с точки зрения размерности.
где
g1 = a1x1 + b1y1 +… + s1z1 g2 = a2x1 + b2y1 +… + s2z1 gl = alx1 + bly1 +… + slz1 Решив эти уравнения, находим критерии подобия по формулам:
Пример: Математическое описание не известно. 1.Определим по методике вектор параметров
2,3 пункты см. выше k =3, m =4. Группа независимых параметров (можно выбрать любые): [ U, R, c ]. Группа зависимых параметров [ I, t, L, w ]. По формуле находим 4 критерия подобия:
Определим p1:
Получим систему уравнений
2x1 + 2y1 - 2z1 = 0 – степени при L x1 + y1 - z1 = 0 – при M -3x1 - 3y1 + 4z1 = 0 – при T -x1 - 2y1 + 2z1 = 1 – при I
Так как 1 и 2 уравнения зависимые, то получим следующую совместную систему: x1 + y1 - z1 = 0 x1 = 1 -3x1 3y1 + 4z1 = 0 Þ y1 = -1 -x1 - 2y1 + 2z1 = 1 z1 = 0
Определим p2:
Получим систему уравнений
2x2 + 2y2 - 2z2 = 0 x2 + y2 - z2 = 0 -3x2 - 3y2 + 4z2 = 1 -x2 - 2y2 + 2z2 = 0
Так как 1 и 2 уравнения зависимые, то получим следующую совместную систему:
x2 + y2 - z2 = 0 x2 = 0 -3x2 3y2 + 4z2 = 1 Þ y2 = 1 -x2 - 2y2 + 2z2 = 0 z2 = 1
Определим p3:
Получим систему уравнений
2x3 + 2y3 - 2z3 = 2 x3 + y3 - z3 = 1 -3x3 - 3y3 + 4z3 = -2 -x3 - 2y3 + 2z3 = -2
Так как 1 и 2 уравнения зависимые, то получим следующую совместную систему:
x3 + y3 - z3 = 1 x3 = 0 -3x3 3y3 + 4z3 = -2 Þ y3 = 2 -x3 - 2y3 + 2z3 = -2 z3 = 1
Определим p4:
Получим систему уравнений
2x4 + 2y4 - 2z4 = 0 x4 + y4 - z4 = 0 -3x4 - 3y4 + 4z4 = -1 -x4 - 2y4 + 2z4 = 0
Так как 1 и 2 уравнения зависимые, то получим следующую совместную систему:
x4 + y4 - z4 = 0 x4 = 0 -3x4 - 3y4 + 4z4 = -1 Þ y4 = -1 -x4 - 2y4 + 2z4 = 0 z4 = -1
Найдем виды критериев по формуле:
1) x1 = 1, y1 = -1, z1 = 0
2) x2 = 0, y2 = 1, z2 = 1
3) x3 = 0, y3 = 2, z3 = 1
4) x4 = 0, y4 = -1, z4 = -1
Рассмотренные положения относятся к случаю заведомо подобных процессов, т.е. определяют необходимые условия существования подобия. В связи с этим возникает вопрос об условиях, не только необходимых, но и достаточных для существования подобия. Такие обстоятельства, кроме равенства критериев, включают в себя требования подобия начальных и граничных условий сопоставляемых процессов. Положения относительно необходимых и достаточных условий подобия изложены в виде первой, второй и третьей теорем о подобии, первые две - определяют необходимые, третья - необходимые и достаточные условия подобия.
Основные теоремы теории подобия
Теория подобия включает три основные теоремы: 1-ая теорема подобия (Теорема Ньютона-Бертранса) о небходимом условии подобия, 2-ая теорема подобия (Пи-теорема), 3-ая теорема подобия (Теорема Кирпичова-Гухмана) о необходимом и достаточном условии подобия.
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.98.91 (0.007 с.) |


 (3.1)
(3.1) (3.2)
(3.2) (3.1а)
(3.1а) (3.2а)
(3.2а) ,
, и
и  , то формула примет вид:
, то формула примет вид: (3.3а)
(3.3а) (3.5а)
(3.5а)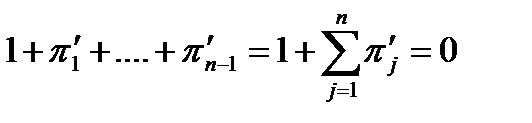 (3.3)
(3.3) (3.4)
(3.4)
 .
. и
и  .
. ;
;  .
. называется “способ интегральных оценок”.
называется “способ интегральных оценок”. - лишние параметры, тогда полный набор параметров P = {i, u, t, L, c, R, ω}, n=7.
- лишние параметры, тогда полный набор параметров P = {i, u, t, L, c, R, ω}, n=7.




 ,
, ,
,

 .
. .
. ,
, ,
,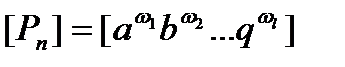 , где l- количество единиц измерения.
, где l- количество единиц измерения. - уравнение для p1,
- уравнение для p1, - известные,
- известные,  - неизвестные величины.
- неизвестные величины. ,
,  , …
, …  .
.
 ,
,  ,
,  ,
,  .
.










 .
.


