
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ранг произведения матриц не превосходит ранг каждого из сомножителей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
rank(AB)<=min(rank(A),rank(B)) Доказательство. Пусть C=AB. Из операции перемножения вытекает, что каждый столбец матрицы C[*,j] есть линейная комбинация ∑А[*,k]. C[*,j]=∑A[*,k]B[k,j]→ rank(C)<=rank(A) – из основной теоремы о линейных пространствах СТ=АТBТ→ rank(C)=rank(CT) <=rank(BТ)=rank(B) α1, α2,…, αn { β1, β2,…,βn rank(α)<=rank(β) Значит rank(AB)<=min(rank(A),rank(B)) Следствие. Пусть С=АВ, если |A|≠0, то rank(C)=rank(B) Доказательство: rank(C)<=rank(B) B=A-1C rank(B)<=rank(C) Значит, rank(B)=rank(C) Аналогично, если |B|≠0, то rank(B)=rank(A) При элементарных преобразованиях ранг матрицы не меняется. С помощью элементарных преобразований матрицу можно привести к квази-треугольной форме. Ранг квази-треугольной матрицы равен r, поскольку ее минор с главной диагональю а11а22,...,аnn равен произведению не равным нулю а все миноры более высокого порядка равны нулю (как содержащие нулевые строки). К элементарным преобразованиям относят следующие: 1) перестановки строк (столбцов); 2) умножение строки (столбца) на число, отличное от нуля; 3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число. Эти преобразования не меняют ранга матрицы, так как известно, что 1) при перестановке строк определитель меняет знак и, если он не был равен нулю, то уже и не станет; 2) при умножении строки определителя на число, не равное нулю, определитель умножается на это число; 3) третье элементарное преобразование вообще не изменяет определитель. Таким образом, производя над матрицей элементарные преобразования, можно получить матрицу, для которой легко вычислить ранг ее и, следовательно, исходной матрицы.
АХ=В (1) A m*n X n*1 B m*1 Система называется однородной, если матрица В=Θ АХ= Θ (2) Если к системе (2) применима правило Крамера, то эта система имеет только нулевое решение. Опр. Общим решением системы (2) нзв. Х(Р₁,...,Р n) и обладающий следующими свойствами: 1) При любом наборе параметров получаем решение системы 2) И наоборот для любого решения х₀ можно подобрать Р°₁,…,Р°n х₀=х(Р°₁,…,Р°n) Предложение: сумма 2ух решений системы (2) явл решением этой системы. Умножив произведение решений системы (2) на число, получим то же самое решение системы АХ₁=Θ АХ₂= ΘАХ₁+ АХ₂=Θ
А(bX₁)=(Ab)X₁=b(AX₁)=Θ, rank(A) = r можно предположить, что первые r строк матрицы А линейно-независимы, то все остальные строки явл линейной комбинацией остальных строк. Все уравнения с номерами больше чем r, явл следствием первых r уравнений. Ранг- максим. число линейно-независимых строк, все остальные явл зависимыми от первых. Вместо исх системы (2) получаем новую систему a₁₁x₁+…+а₁ᵣxᵣ+a₁ᵣ+1xr+1+a1nxn=0 (3) a21x1+…+а2rxr+a2 r+1xr+1+a2nxn=0 ar1x1+….+arrxr+…arnxn=0 в первой было m уравнений,а в(3) r Ar представили в блочном виде, Ar=(A1,A2) A1= Вектор х разобъём на 2 части Х= Система (4)- краткая запись A1X1+A2X2=Θ >> A1X1=-A2X2 (5) >> |A1|≠0 1 шаг - нашли ранг (из всех уравнений берём только r), 2 шаг-преобразовали в (5) Теорема: Пусть дана однородная система уравнений (2),если ранг матрицы равен r, то общее решение системы имеет вид X(P1,…Pn-r)= P1Z1+P2Z2+…+Pn-rZn-r Построение решения: если в системе (5) в качестве вектора х2 взять любой вектор длины n-r, то решая систему (5) по правилу Крамера мы находим вектор х0, и составляя из них хon= D (n-r)×(n-r), |D|≠0, AX1=-A2D[*|i], i=1,…,n-r Yi ( Y= Док-ть, что любое решение можно представить в этом виде [Пусть z-любое решение AZ=Θ Z=( 1часть имеет длину r, 2 часть имеет длину (n-r) A1Z1=-A2Z2 По построению определитель матр D≠0, значит его столбцы матр В линейно-независимы, следовательно столбцы образуют базу в пространстве столбцов длины (n-r), значит вектор z2 можно представить как Z2= cj - коэффициент разложения по базе вектор W=Z- AW=Θ A1W1=-A2W2 W2=Z2- Любое решение системы(1) представимо в виде(2) ] Число Yi- совпадает с числом столбцов в В. В формуле (2) число слагаемых =(n-r),а сами решения Yi нзв фундаментальными решениями bi-степени свободы. При практическом построении фунд решений обычно в качестве матр D выбирают единичную матрицу порядка n-r
|
|||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 1849; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.212.203 (0.006 с.) |

 r×к >> A2=
r×к >> A2=  ) r×(n-r)
) r×(n-r)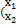 ) >> x1=r×1 >> x2=(n-r)×r >> (A1|A2)(
) >> x1=r×1 >> x2=(n-r)×r >> (A1|A2)(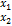 )=Θ
)=Θ )
) ) было доказано, что любая линейная комбинация решений однородной системы явл решением той же самой системы
) было доказано, что любая линейная комбинация решений однородной системы явл решением той же самой системы (2) решение системы (1)
(2) решение системы (1) )
)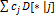
 каждый из векторов, есть решение системы (1)
каждый из векторов, есть решение системы (1)


