
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства определителя n-ого порядка.Стр 1 из 6Следующая ⇒
Ранг матрицы. Две системы векторов α и β называются эквивалентными, если каждый вектор α{ β(выражается) и β{ α. Предложение. Ранги эквивалентных систем совпадают. αi1, αi2,…, αir – МЛНП α, βi1, βi2,…, βik – МЛНП β, αi1, αi2,…, αir < β < βi1, βi2,…, βik → r<=k Поменяв местами α и β местами → r>=k >>> Значит, r=k. Определение. Пусть дана матрица A= αi=<ai1,ai2,…ain> Рангом матрицы А называется ранг системы векторов α1, α2,…, αm, составленных из это матрицы >>rank(A)-ранг Из определения очевидно, что при перестановке столбцов ранг не меняется. Покажем, что при перестановке столбцов ранг так же не меняется. А’= α’i=<a1n, ai2,…,ai1> Линейно зависимы: b1α1+ b2α2+…+ bmαm=θ, b1а11+b2a21+…+bmam1=0, b1α’1+ b2α’2+…+ bmα’m, b1а11+b2a21+…+bmam1=0 Основная теорема о рангах матрицы. Ранг матрицы совпадает с максимальным порядком отличных от нуля миноров этой матрицы. Док-во: предположим, что в матрице имеется минор n-го порядка не равный нулю, а все его более высокие миноры нулевые. Доказат ь, что ранг матрицы равен n. Переставляя строки и столбцы, можем переместить этот минор в левый верхний угол.
D= Докажем, что первые r строк линейно независимы и что любая другая строка линейная комбинация этих r строк: если бы первые r строк были линейно зависимы, то какая то строка была линейной комбинацией остальных, тоже самое было бы справедливо для выделенного минора и он равнялся 0. Докажем, что любая строка есть линейная комбинация этих строк: α1=<ai1,ai2,…,air> Составим определитель (добавим i-тую строку) D1= Если j<=r в определителе два одинаковых столбца и определитель равен 0 Если i>r, то минор r+1 порядка и равен 0. D1=0=a1j(-1)r+2 D1(1|r+1)+a2j(-1)r+3D1(2|r+1)+…+aij(-1)2r+2D (D≠0) aij= Вся i-тая строка есть линейная комбинация первых r строк Следствие.1) При транспонировании матрицы ранг не меняется (Ранг матрицы можно определять ка по строкам, так и по столбцам 2)Определитель квадратной матрицы равен 0, тогда и только тогда, когда какая-то строка матрицы является линейной комбинацией остальных. (Необходимое и достаточное условие равенства нулю определителя квадратной матрицы) Доказательство. Дана матрица А n×n. |A|=0
Если |A|=0, то максимальный порядок не равных нулю миноров меньше n. Из основной теоремы следует, что rank(A)<n.Значит, строки матрицы линейно зависимы и определитель равен 0. Ранг произведения матриц. Система координат. Сист. коорд. в аффинном пр-ве нзв. точка О (начало коорд) и базис в пр-ве векторов. Часто сист. коорд. на пл-ти задают двумя пересекающимися прямыми, начало коорд. есть точка пересечения прямых, а базисные векторы имеют единичную длину и //ны соответ. прямым. Если выбрана сист. коорд., то каждая точка Р получает коорд.: это коорд. вектора, идущего из начала в эту точку, подсчитанные в выбранной базе. ОР = aα + bβ α β O Р u cmV2LnhtbEyPQU/DMAyF70j8h8hI3La0ZRqjNJ0QY2fEAIlj1pi2kDhVkm3tv8c7sZvt9/T8vWo9 OiuOGGLvSUE+z0AgNd701Cr4eN/OViBi0mS09YQKJoywrq+vKl0af6I3PO5SKziEYqkVdCkNpZSx 6dDpOPcDEmvfPjideA2tNEGfONxZWWTZUjrdE3/o9IDPHTa/u4NTEG378jN9Tn5TmDBttvELX/OF Urc349MjiIRj+jfDGZ/RoWamvT+QicIqmOXL1T17FdzlXOrsyIoFT3u+POQg60pedqj/AAAA//8D AFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9U eXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9y ZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhADNqlFv0AQAA9QMAAA4AAAAAAAAAAAAAAAAALgIAAGRy cy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhANvi7WTeAAAACwEAAA8AAAAAAAAAAAAAAAAATgQA AGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAABZBQAAAAA= " strokecolor="#4579b8 [3044]"/> Свойства определителя n-ого порядка. 1.|A|=|AT| При транспонировании матрицы, определитель не меняется. Пусть B=AT → B[i|j]=A[j|i] |B|=Σ± B[1|i1]..B[n|in]= Σ±A[i1|1]..A[in|n]→|B|=|A| 2.Если какая-то строка матрицы состоит из 0,то определитель =0. A[k|*]=0→|A|=0. Каждое слагаемое содержит элемент k-ой строки, поэтому все произведение=0. 3. A[k|*]→cA[k|*] = |A|→c|A| 4.Если в матрице поменять местами 2 строки, то определитель матрицы поменяет знак. B[i|*]=A[i|*],i≠k,i≠j. B[k|*]=A[j|*] B[j|*]=A[k|*] |B|=Σ± B[1|i1]..B[k|ik]..B[j|ij]..B[n|in]=Σ±A[1|i1]..A[j|ik]..A[k|ij]..A[n|in]= -Σ±A[1|i1]..A[j|ik].. A[k|ij]..A[n|in]= -|A| 5.Если в матрице есть 2 одинаковые строки, то ее определитель равен 0. Поменяем местами равные строки |A|= -|A|→|A|=0 6. A[i|*]=A′[i|*]+A′′[i|*]. |A|= Σ±A[1|j1]..A[i|ji]..A[n|jn]= Σ±A[1|j1]..(A′[i|ii]+A′′[i|ii])..A[n|jn]= Σ±A[1|j1]..A′[i|ji]..A[n|jn]+ Σ±A[1|j1]..A′′[i|ji]..A[n|jn] 7.Если какая-то строка матрицы есть линейная комбинация остальных, то определитель=0. A[n|*]=ΣbkA[k|*] 8.Если к какой-то строке матрицы прибавить линейную комбинацию остальных, то определитель не меняется. A[n|*]→ A[n|*]+ΣbkA[k|*] Определитель треугольной матрицы. Матрица называется верхней треугольной, если все элементы ниже главной диагонали нулевые. |A|=Σ±a1i1∙a2i2..anin=Σ±a1i1..an-1in-1∙ann=Σ±a1i1..an-1n-1∙ann=a11∙a22..ann Определитель = произведению диагональных элементов.
Разложение определителя по строке. Теорема: для любой кв.матрицы справедливы формулы: |A|=ΣiA[i|j]Aij= ΣjA[i|j]Aij Рассмотрим частный случай 1.(в последнее строке все столбцы нулевые кроме последнего)|A|= Σ±a1i1∙a2i2..anin=Σ±a1i1..an-1in-1∙ann= ann Σ±a1i1..an-1in-1= ann|A(n|n)|= annA(n|n) 2.(из матрицы A iый столбец перенесли в конец, получили матрицу B) |B|=aniBnn |B|=(-1)n-i|A|=ani|A(n|i)| |A|= aniAni. (ani,an2..ann)=(ani,0..0)+(0,an2..0)+..(0,0..ann) |A|=ΣankAnk
1 1 … 1 Вычитая первый столбец из всех последующих получаем Δ(x1,x2,…,xn)= x1 x2 … xn первую строку равную 1 0…0 все последущии х1п-1 …хпп-1-х1п-1 x1n-1 x2n-1… xnn-1 далее разложение по 1-ой строке после вычитаем из каждой строки предыдущую строку умноженную на x1 далеемы можем вынести за знак определителя общий множитель первого столбца равный (x2-x1) общий множитель второго столбца x3-x1 и т.д.в рез-те получим Δ(x1,x2… xn)=(x2-x)(x3-x1)…(xn-x1)Δ(x2,x3…xn) со стоящим в правой части определителем поступим так же,продолжая такие рассуждения далее окончательно получим исходный определитель det(A)=(x2-x1)(x3-x1)…(xn-x1)(x3-x2)…(xn-x2)…(xn-xn-1) Определитель Вандермонта. Обратная матрица Определение: Матрица B называется обратной матрицей для квадратной матрицы А, если Из определения следует, что обратная матрица A будет квадратной матрицей того же порядка, что и матрица Предложение Если матрица Доказательство. Так как определитель произведения матриц равен произведению определителей, то Последнее предложение можно сформулировать в следующем виде.
|
||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.159.150 (0.018 с.) |



 ≠0
≠0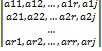 1<=j<=r
1<=j<=r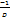 (a1j(-1)r+2 D1(1|r+1)+a2j(-1)r+3D1(2|r+1)+…)
(a1j(-1)r+2 D1(1|r+1)+a2j(-1)r+3D1(2|r+1)+…) .
. (иначе одно из произведений
(иначе одно из произведений 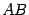 или
или  было бы не определено). Обратная матрица для матрицы
было бы не определено). Обратная матрица для матрицы  . Таким образом, если
. Таким образом, если 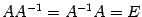 . Из определения обратной матрицы следует, что матрица
. Из определения обратной матрицы следует, что матрица 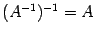 . Про матрицы
. Про матрицы  и
и 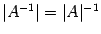 .
.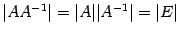 .
.  , поэтому
, поэтому  , что невозможно при
, что невозможно при  . Из предыдущего равенства следует также
. Из предыдущего равенства следует также 


