
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Запасные части и контроль изделий в процессе эксплуатации.Содержание книги
Поиск на нашем сайте
Важной составной частью осуществления принципа взаимозаменяемости, обеспечивающего долговечную и экономичную работу изделий, является определение необходимого комплекта запасных частей (деталей и составных частей), которые гарантировали бы быструю замену в процессе эксплуатации износившихся или поломанных деталей или составных частей, сохраняя требуемую работоспособность машины в течение длительного времени. Для этого должен быть проведен анализ и выявлены «слабые места» изделия, т. е. найдены детали и составные части, в наибольшей мере подверженные износу и ухудшению качества, и влияющие на эксплуатационные показатели. В процессе эксплуатации необходимо тщательно контролировать работу машины и особое внимание уделять наиболее «слабым» элементам. Ремонт износившихся частей машин и других изделий целесообразно проводить на специальных ремонтных заводах. Для практического осуществления принципа функциональной взаимозаменяемости изделий необходима четкая система конструкторской, технологической, метрологической и эксплуатационной документации. Содержание.
Литература:
А. И. Якушев, «Взаимозаменяемость, стандартизация и технические измерения», М., «Машиностроение», 1979 Содержание.
Технические измерения
Методические указания Взаимозаменяемость – фундаментальное понятие теории точности. Т очностью детали приборов называется их свойство обеспечивать в допустимых пределах погрешность расположения и движения выходных звеньев при определенных законах движения входных звеньев. При изготовлении деталей и в процессе их эксплуатации происходят отклонения размеров и их формы звеньев, возникают деформации, изменяется характер сопряжения деталей. Все это приводит к изменению кинематических и динамических параметров деталей приборови влияет на точность выполнения ими заданных функций. Точность узлов ИП оценивается значениями ошибок положения, перемещения, передаточного числа и мертвым ходом. Повышение точности узлов достигают снижением погрешностей изготовления деталей. Отметим, что для механизмов систем автоматики и робототехники точность является одним из основных показателей качества деталей. В опросы для самопроверки 1. П араметры точности деталей ИП? 2. С пособы повышения точности изготовления деталей ИП? 3. В заимосвязь функций деталей с точностью их изготовления? ТЕХНИЧЕСКИЕ ИЗМЕРЕНИЯ С ОВРЕМЕННЫЕ ТЕХНИЧЕСКИЕ ИЗМЕРЕНИЯ (2 часа) О сновные положения. Современные технические измерения физических величин. Важно понять, что показатели технических измерений определяют показатели производственных технологий. А применяемые измерительные приборы как основа технических измерений определяют их ОСНОВНЫЕ метрологические характеристики. В опросы для самопроверки 1. К акие зарубежные приборы Вы знаете? 2. С равните два мультиметра по особенностям их конструкции? 3. К акие приборы в лаборатории кафедры Вам известны? 9. ОСНОВНЫЕ ЭТАПЫ ПРОЕКТИРОВАНИЯ И КОНСТРУИРОВАНИЯ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ (2 часа) Современные форматы конструирования и проектирования приборов и их деталей и узлов. Основные требования Государственной системы стандартизации (ГСС) к проектированию и производству продукции. 9.1. Об О СНОВАХ КОНСТРУИРОВАНИЯ ПРИБОРОВ К онструирование деталей и узлов с данной целевой функцией важнейший этап структурно-кинематического и конструкторско-технологического уровней. Методы автоматизированного (интеллектуального) конструирования. Методы оптимизации сборки узлов приборов с помощью ПЭВМ. Примеры и задачи. Характеристики конструктивного качества и экономической эффективности конструкции ИП. Расчет общей и метрологической надежности деталей, входящих в механизмы ИП. Единая система конструкторской документации - ЕСКД. Виды изделий, стадии разработки и проектирования, этапы работ. Порядок проведения научно исследовательских работ - НИР, опытно-конструкторских работ - ОКР. Единая система технологической документации - ЕСТД, основные положения. Примеры и задачи. В опросы для самопроверки 1. Ц елевая функция конструирования ИП? 2. К ак можно использовать компьютер для конструирования ИП? 3. В ка ких системах можно конструировать на компьютере? РАСЧЕТЫ ПРИ КОНСТРУИРОВАНИИ ПРИБОРОВ (8 часов) [ О. – Л. 3 (с. 84-94)] О СНОВЫ ТЕОРИИ И РАСЧЕТА 9.2. О СНОВЫ ПРОЕКТИРОВАНИЯ ПРИБОРОВ О проектировании современных детали приборов на основе достижений электроники, кибернетики автомеханического регулирования и управления. Роль методов автоматизированного проектирования при создании конструкций оптимальных детали приборов и приборов. [О. - Л. 21 (с.)]. Структурный и конструкторско-технологический уровни проектирования. Методы автоматизированного конструирования и оптимизации приборов с помощью ПЭВМ. Единая система программной документации – ЕСПД. Общие сведения. Оформление, содержание и правила выполнения программных документов. Характеристики конструктивного качества и экономической эффективности конструкции. Расчет надежности приборов. Перспективы развития современных систем полного автоматического проектирования (проектирование – изготовление-эксплуатация) [ О. - Л. 3 (с. 249-358)]. В опросы для самопроверки 1. К акие направления конструирования ИП Вы изучили? 2. К ак можно использовать компьютер для конструирования? 3. К акие приборы Вы хотите конструировать? Функции передаточных механизмов в приборах. Основные требования к конструкциям передаточных механизмов. Большинство современных приборов представляет собой сложные комплексы, в которых сочетаются электрические, пневматические, оптические и другие измерительные цепи с механическими цепями или передаточными механизмами. От качества механизма в значительной степени зависит и качество всего измерительного комплекса. Если основное назначение механизма в машине состоит в передаче энергии от двигателя к рабочему органу с одновременным преобразованием скоростей движения звеньев, то в измерительных устройствах приборов передаточные механизмы выполняют: преобразование принятого электрического (пневматического, гидравлического и т. д.) сигнала в движение механизма и передачу его на исполнительный орган; преобразование измеряемых характеристик механического сигнала (перемещения скорости, ускорения) в соответствующий электрический или иной сигнал; математические операции (суммирование, логарифмирование, дифференцирование и т. д.); ряд эксплуатационных операций (включение или выключение системы, переключение диапазонов, осуществление ручной или автоматической настройки, осуществление дистанционирования при управлении измерительной системой и др.). К конструкциям передаточных механизмов предъявляют следующие требования: заданной точности преобразования движения по известной функциональной зависимости; достаточной прочности и жесткости элементов механизма при передаче усилий или моментов; простоты и надежности регулировки, высокого КПД, малой чувствительности к температурным изменениям и вибрациям; технологичности конструкции, минимальных габаритных размеров и массы, наименьшей стоимости изготовления. При разработке конструкции передаточного механизма необходимо иметь в виду, что выполнение всех перечисленных выше требований затруднительно, так как некоторые из них могут противоречить друг другу. Например, повышение точностных характеристик всегда приводит к увеличению стоимости изготовления;
повышение прочности и жесткости отдельных звеньев приводит к увеличению габаритов и массы; нечувствительность к температурным изменениям достигается за счет введения специальных компенсационных узлов, что безусловно усложняет механизм и т. д. Разработка оптимальных вариантов конструкций передаточных механизмов может быть выполнена только применительно к конкретной задаче с учетом условий изготовления и эксплуатации прибора. Анализ всего многообразия реальных передаточных механизмов, приборов и установок показывает, что их механические цепи состоят из первичных, как правило, трех- или четырехзвенных механизмов, соединенных между собой. На рис. 43, а показано наиболее распространенное последовательное соединение п первичных механизмов, с характеристиками ух = ух (х); уъ = уг (уг)... уп (уп — 1) и передаточными отношениями U1,0; U2,1;...; Un, (n – 1), а для всей цепи
На рис. 43, б показано параллельное соединение первичных механизмов с характеристиками ух — ух (х); уг — уг (х)... уп = уп (х) и передаточными отношениями U1,0, U 2,0; U30,..., U n, 0, а для всей цепи
На рис. 43, б показано встречно-параллельное соединение двух механизмов с характеристиками у = у (хх) и х2 = х2 (у) и передаточными отношениями Uy хl, и
Uх2, y, а для всей двухэлементной ячейки
На практике часто встречаются так называемые многопоточные механизмы, в которых на каком-то этапе преобразования движения появляется несколько ветвей, не связанных между собой на конце и имеющих самостоятельные выходы (рис. 44). Анализ в этом случае проводится независимо по каждой ветви с использованием формул (28)—(30).
Классификация элементарных передаточных механизмов Все элементарные передаточные механизмы можно классифицировать по ряду признаков, например по конструктивному выполнению, кинематическим и динамическим параметрам, точности и т. д. Наиболее важными из этих признаком являются конструктивный и кинематический. По конструктивному признаку все передаточные механизмы могут быть разделены на восемь групп (рис. 45). В свою очередь, все группы, кроме одной (винтовые механизмы), подразделяются на подгруппы. Передаточные механизмы можно также классифицировать по виду преобразования движения и по преобразованию скорости. По виду преобразования движений: а) вращательного во вращательное (зубчатые: колесо—триб, сектор—триб; червячные, кулачковые с качающимся роликом и т. д.); б) вращательного в поступательное (кривошипно-шатунные, в) поступательного во вращательное (синусные и тангенсные, г) поступательного в поступательное (двойные синусные или По преобразованию скорости движения: а) с постоянным отношением скоростей (зубчатые, фрикционные, червячные и т. д.);
б) с переменным отношением скоростей. Характерная особенность механизмов с переменным отношением скоростей состоит в том, что одно из звеньев (ведущее или ведомое) находится в равномерном движении, в то время как скорость движения другого звена может подчиняться любому более сложному заданному закону (например, механизмы синусные и тангенсные, поводковые, кривошипно-шатунные; кулачковые и т. д.). К этой же группе относятся механизмы прерывистого движения, у которых равномерное движение ведущего звена преобразуется в пульсирующее (с остановками) движение ведомого (мальтийские и храповые механизмы).
Рычажные механизмы
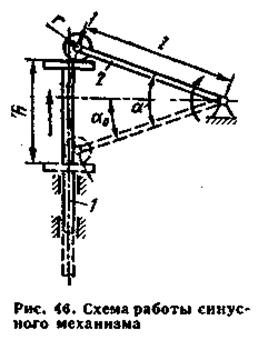
Примером механизма с постоянным передаточным отношением является двойной синусный или тангенсный механизмы. Механизмы с переменным передаточным отношением встречаются чаще первичных и отличаются конструктивными особенностями. Точность рычажного механизма зависит от погрешности передаточного отношения, которая, в свою очередь, определяется погрешностью изготовления элементов передачи, жесткостью системы, погрешностями от изменения температуры и погрешностями, возникающими за счет действия сил трения. Синусные механизмы (рис. 46) служат для преобразования поступательного движения во вращательное и состоят из толкателя 1, движущегося поступательно, и рычага 2 со сферическим наконечником радиуса r, находящегося в колебательном движении. Ведущим звеном может являться как толкатель, так и рычаг. Определим характеристику и передаточное отношение синусного механизма, т. е, зависимость между перемещением толкателя h и углом поворота рычага l на угол α:
Как видно из этого уравнения, характеристика синусного механизма не зависит от радиуса сферического наконечника рычага.
Величина передаточного отношения не остается постоянной. Его мгновенное значение определяется положением звеньев механизма (углом поворота а). Минимальное значение U2,1min соответствует положению механизма, при котором α = α0: U2,1min = Изменение мгновенного передаточного отношения при повороте рычага определяют с помощью выражения
Подставляя в последнее выражение значения U2,1 и U2,1min, имеем
Кривые изменения δ U2,1 в зависимости от α и α, показаны на рис. 47. Как видно из графика, начальное положение рычага необходимо выбирать такое, чтобы Синусные механизмы применяют в сильфонных манометрах, центробежных тахометрах, электроконтактных датчиках, автоматических и счетно-решающих устройствах. Тангенсные механизмы применяют для тех же целей, что в синусные. В отличие от последних, в которых точка контакта при работе механизма перемещается по плоской поверхности толкателя, в тангенсных механизмах она скользит по рабочей поверхности рычага.
На рис. 48, а показана схема тангенсного механизма, характеристика которого определяется следующей зависимостью:
Передаточное отношение тангенсного механизма для случая, когда ведущим является толкатель:
Максимальное значение U2,max соответствует положению механизма, при котором а = а0:
Найдем изменение мгновенного передаточного отношения тангенсного механизма при повороте рычага:
Двойные тангенсные механизмы. На рис. 48, б показана схема рычажного механизма, представляющего собой комбинацию двух тангенсных механизмов. Он состоит из рычага 2, передающего движение от ведущего толкателя 3 к ведомому толкателю 1. Передаточное отношение для любого положения рычага остается постоянным:
Погрешность передаточного отношения для механизмов этого типа не зависит от температурных изменений, так как при изменении плеч рычагов их отношение остается постоянным и будет определяться изгибом рычагов и ошибками изготовления плеч l1 и l2. В реальной конструкции рычажного механизма стержни, соприкасающиеся с рычагом, обычно имеют сферический наконечник. При повороте рычага на угол а (рис. 48, в)точка касания смещается. В результате передаточное отношение изменяется. Пусть вначале рычаг находится в горизонтальном положении и его передаточное отношение U0 = l2/l1. При повороте рычага на угол α точки касания стержней и рычага сместятся на величины Δ l1 и Δ l2. Передаточное отношение
Подставляя в последнее выражение получим
Изменение передаточного отношения
В рассматриваемом случае уменьшение ошибки переда точного отношения достигается уменьшением радиусов r1 и r2и углы поворота рычага а. Поэтому применяют ножевые опоры, которое имеют малый радиус закругления порядка 0,5—5 мкм. Постоянство передаточного отношения рычажного механизма при использовании сферических наконечников сравнительно больших радиусов достигается их расположением, как показано на рис. 48, в. При этом передаточное отношение и его погрешность равны погрешности передаточного отношения δ U2,1 при условии, если l1r2 = l2r1. Таким образом, конструктивная погрешность передаточного отношения равна нулю, когда радиусы сферических наконечников пропорциональны длинам плеч рычагов. Кривошипно-шатунные механизмы Кривошипно-шатунные механизмы являются наиболее распространенными механизмами, применяемыми в машинах и приборах для преобразования поступательного движения во вращательное или вращательного движения в поступательное. На рис. 49 показаны схемы кривошипно-шатунного механизма, состоящего из кривошипа ОА, шатуна АВ и ползушки В. В этом механизме ведущим звеном может являться как кривошип, так и ползушка. Если центр вращения кривошипа О лежит на оси ползушки В, то такой механизм называют простым или аксиальным (рис. 49, а), для которого характеристика может быть найдена проектированием звеньев на координатные оси. При проектировании звеньев на ось ох имеем
где h — перемещение ползушки. При проектировании на оси оу
Решая полученные уравнения совместно, находим характеристику механизма
Передаточное отношение механизма, у которого ведущим звеном является кривошип, находим по формуле
где Если же ведущим звеном является ползушка В, то
Из уравнения следует, что передаточное отношение кривошипно-шатунного механизма непостоянно и зависит от отношения длин кривошипа и шатуна, а также угла поворота ведущего звена а. Передаточное отношение для принятого начального положения механизма ОА0В0 при α = 0 U α=0 = α Тогда относительное изменение передаточного отношения
Из анализа последнего уравнения следует, что с уменьшением k рабочий угол механизма увеличивается, поэтому на практике значения k выбирают не более 1/5—1/3. Если принять k < 1/3, то передаточное отношение механизма может быть определено с достаточной для практических расчетов точностью по приближенной формуле
В приборах часто применяются дезаксиальные кривошипно-шатунные механизмы, в которых ось вращения кривошипа О смещена относительно оси ползушки В на величину d, называемую дезаксиалом (рис. 49, б). Характеристика дезаксиального механизма может быть найдена аналогично аксиальному кривошипно-шатунному механизму и имеет следующий вид:
тогда передаточное отношение
где
Во многих дезаксиальных кривошипно-шатунных механизмах для уменьшения изменения δU величину дезаксиала выбирают равной длине кривошипа, т. е. т = 1. Принимая значения k =1/3 и m =1 передаточное отношение для этого механизма можно определить по следующей приближенной формуле:
Кривошипно-шатунные механизмы применяют во многих приборах, где чувствительными элементами являются манометрические трубки, мембраны, сильфоны и другие упругие элементы. На рис. 51 показана схема центробежного тахометра, в котором в качестве чувствительного элемента использована кольцевая масса 8. Вращение рабочей оси 13 через зубчатую передачу 12 передается на ось. 9 чувствительного элемента и вызывает поворот кольцевой массы 8 вокруг оси // на угол Щ, величина которого пропорциональна числу оборотов. Противодействующий момент в тахометре создается спиральной пружиной 10. Поворот кольцевой массы 8 с помощью дезаксиального кривошипно-шатунного механизма, в котором кривошипом служит кольцо (размером а), а Кулисные механизмы.
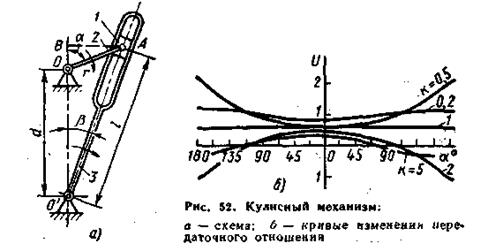
Кулисные механизмы применяют в приборах и машинах для передачи вращательного движения с одной оси на другую с преобразованием закона движения. Кулисный механизм (рис. 52, а) состоит из кулисы 3 и рычага 2, несущего на конце ползушку 1, которая скользит в прорези кулисы. Проектируя звенья на ось 00', после преобразований получим характеристику механизма
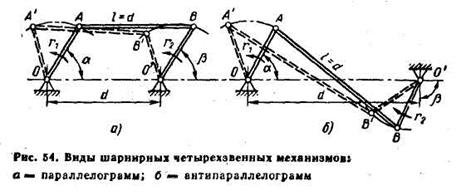
: Передаточное отношение в кулисном механизме можно считать практически постоянным при углах поворота рычага в пределах ±45º. При проектировании передаточных механизмов с переменным передаточным отношением необходимый закон изменения U получают подбором отношения d/r и выбором рабочего угла поворота α. Шарнирные четырехзвенные механизмы. Шарнирные четырехзвенные механизмы применяют в приборах и различных узлах машин для преобразования вращательного движения ведущего звена — кривошипа ОА в колебательное движение ведомого звена — коромысла или балансира О'В (рис. 53). Связь между Ведущим и ведомым звеньями осуществляется шатуном АВ, находящимся в плоскопараллельном движении относительно неподвижной стойки. На рис. 54 показаны разновидности четырехзвенных механизмов. Для передачи вращательного движения с оси О на ось О'' с постоянным передаточным отношением служит шарнирный параллелограмм (рис. 54, а). Направление вращения может быть изменено с помощью «обратного» параллелограмма (рис. 54, б). Условия нормальной работы этих механизмов: l = d и r1 = r2. Найдем характеристику β = f (α) шарнирного четырехзвенного механизма, изображенного на рис. 55. Из треугольников О'АО и О'В А соответственно имеем γ = arcsin
механизма имеет вид
где Передаточное отношение механизма U = получено дифференцированием выражения. Учитывая трудоемкость математических преобразований, возникающих в процессе дифференцирования, рассмотрим метод определения передаточного отношения с помощью мгновенного центра скоростей (МЦС). Для этой цели выразим передаточное отношение через отношение линейных скоростей точек А и В:
МЦС для шатуна АВ находится в точке М, поэтому, заменяя отношение линейных скоростей отношением расстояний от точек А и В до МЦС,
получим
Из треугольника МОО' имеем
а так как
и
то, подставляя значения ВМ и AM в выражения для U2,1 после преобразований получим
Рассмотренный метод определения передаточного отношения через МЦС является универсальным и может быть применен при исследовании различных передаточных механизмов приборов. Из уравнений (31) и (32) видно, что передаточное отношение зависит от большого числа различных геометрических параметров (длины кривошипа, балансира, шатуна и базового размера), поэтому дать общие рекомендации по выбору размеров отдельных звеньев механизма затруднительно.
В поводковом механизме (рис. 56, а) движение с ведущего вала 1 передается на ведомый вал 2 с помощью поводков 3 и 4, представляющих собой стержни одного диаметра, оси которых либо перпендикулярны к осям валов 1 и 2, либо одна из осей (чаще ось ведущего поводка) наклонена под углом γ ≠ 90°. Точки пересечения А и В осей поводков с осями соответствующих валов находятся на расстояниях а и Ь от точки пересечения осей валов О. При повороте ведущего вала 1 на угол а ведомый вал 2 поворачивается на угол β, в общем случае не равный углу α. Характеристика поводкового механизма имеет вид
Тогда передаточное отношение механизма
Передаточное отношение не является величиной постоянной и зависит от ряда параметров механизма. К их числу относятся: угол поворота ведущего поводка α, отношение длин поводков b/а, угол наклона оси ведущего поводка γ. На рис. 56, б приведены кривые зависимости передаточного отношения от этих параметров. Из графиков видно, что передаточное отношение резко изменяется с увеличением отношения b/а. В зависимости от угла наклона у можно выделить два семейства кривых, соответствующих значениям γ > 90° и γ < 90°. Семейство кривых при γ < 90° может быть использовано при проектировании поводковых передач в приборах с постоянным значением U, а семейство кривых при γ > 90° — в приборах с переменным U для получения необходимой характеристики шкалы. Поводковые механизма благодаря простоте изготовления применяют в приборах, заменяя зубчатые механизмы с коническими колесами при ограниченных углах поворота. Несмотря на наличие трения скольжения в точке контакта поводков, КПД этих механизмов достаточно высок и достигает 92—96%. Винтовые механизмы В винтовых механизмах используют винтовые кинематические пары 5-го класса. Они обычно служат для преобразования вращательного движения в поступательное с весьма значительным уменьшением скорости. Основными деталями винтового механизма являются: цилиндр с наружной резьбой (винт) и кольцо с внутренней резьбой (гайка). Ш зависимости от характера движения винта и гайки механизмы подразделяют на 4 группы: с вращающейся гайкой и поступательно движущимся винтом (рис. 57, а); с вращающимся винтом и поступательно движущейся гайкой (рис, 57, б); с неподвижным винтом и гайкой, находящейся в винтовом движении (рис. 57, в); с неподвижной гайкой и винтом, находящимся в винтовом движении (рис. 57, г).
В винтовых механизмах применяют следующие виды резьб. Резьбу метрическую применяют для крепежных деталей заход (рис. 58). Основные параметры метрической резьбы: d —наружный диаметр; S—шаг резьбы; Н — теоретическая высота резьбы, определяется из соотношения d8 — средний диаметр резьбы
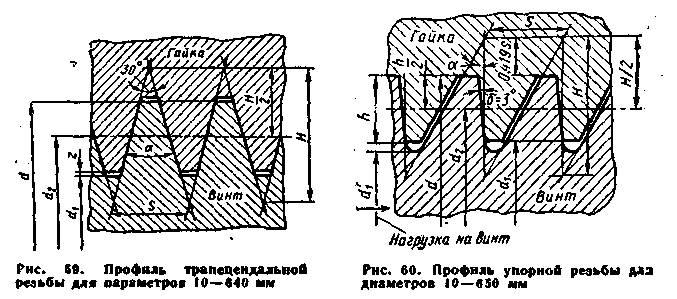
По ГОСТу резьба с одним наружным диаметром может иметь различные шаги. Например, резьба с d = 10 мм может иметь S = 0,5; 0,75; 1; 1,25 и 1,5 мм. Резьбу с максимальным или крупным шагом обозначают размером наружного диаметра: М10, М12 и т. д. Резьбу с мелким шагом обозначают размером наружного диаметра и шага: М10Х1.25; М10Х0.5 и т. дг Резьбу трапецеидальную применяют исключительно для винтовых механизмов, чаще в силовых конструкциях, если осевая сила может действовать в любом направлении (рис. 59). В трапецеидальной резьбе, как и в метрической, стандартом определены d, S и а = 30°. Остальные параметры резьбы определяют по приведенным ниже зависимостям: Теоретическая высота Н = 1,866S; h — 0,5S. Глубина резьбы hx — 0,5S + z. Зазор z = 0,25 мм для резьб с S = 2-=-4 мм, z = 0,5 мм для резьб с S = 5-Г-12 мм и г = 1 для резьб с S = 16 мм и более. Средний диаметр da=d—0,5S.
Внутренний диаметр резьбы винта d\ = d — 2h — 2z. Внутренний диаметр резьбы гайки d' — d + 2z. Наружный диаметр резьбы гайки dx = d — 2/i.
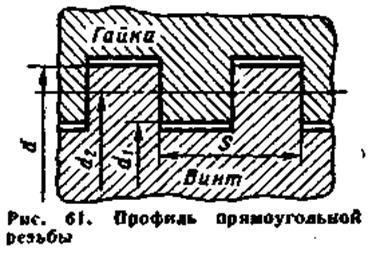
Винтовые механизмы с трапецеидальными резьбами имеют более высокий КПД, чем с метрическими, но ограничены минимальным размером d = 10 мм. Количество параллельных ниток резьбы или заходов, как правило, не превышает четырех. Трапецеидальная однозаходная резьба обозначается размером наружного диаметра и шага, например «трап 60x12». В обозначение многозаходной резьбы вводится дополнительно число заходов, например «трап 60 X (2x12)». 3. Резьбу упорную (рис. 60) используют для тяжелонагруженных винтовых механизмов с осевыми силами, действующими в одном направлении (прессы, механизмы вакуумных задвижек и т. д.). Угол профиля а располагается односторонне по отношению к осевому сечению и равен 30°. Основные геометрические параметры резьбы определяют из соотношений: Н=l,588S; h1 = 0,868S; h = 0,75S. По аналогии с трапецеидальной введем условное обозначение упорной резьбы, например, «уп. 80 X (2 х 16)». 4. Резьбу ленточную, или прямоугольную (рис. 61) применяют с 5. Специальные резьбы служат для соединения труб, арматуры трубопроводов и фитингов. К этой группе крепежных резьб относятся трубные цилиндрические резьбы (рис. 62). Их обозначают по внутреннему раз К специальным резьбам относятся также круглые резьбы (рис. 63), применяемые в цоколях электроламп и некоторых других случаях. Силовые зависимости в винтовых механизмах. При использовании резьб в силовых винтовых механизмах основной задачей является определение момента М, действующего на вращающуюся деталь (винт или гайку) для получения определенной осевой нагрузки Q. Развернув один виток резьбы, получим клинов
|
|||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.255.247 (0.014 с.) |







 В рычажных механизмах для преобразования движения используют один или несколько равноплечих или неравноплечих рычагов, В рычажных системах передаточное отношение может оставаться постоянным или изменяться по определенному закону.
В рычажных механизмах для преобразования движения используют один или несколько равноплечих или неравноплечих рычагов, В рычажных системах передаточное отношение может оставаться постоянным или изменяться по определенному закону.
 Передаточное отношение механизма для случая, когда ведущим является толкатель, найдем дифференцированием:
Передаточное отношение механизма для случая, когда ведущим является толкатель, найдем дифференцированием:
 .
.
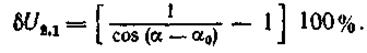
 . Например, при угле поворота синусного механизма атях = 30°, когда α0 = 0, изменение передаточного отношения достигает 16%, а при повороте механизма на тот же угол атях = 30°, при α0 = 15° величина δ U2,1 не превышает 4%.
. Например, при угле поворота синусного механизма атях = 30°, когда α0 = 0, изменение передаточного отношения достигает 16%, а при повороте механизма на тот же угол атях = 30°, при α0 = 15° величина δ U2,1 не превышает 4%.
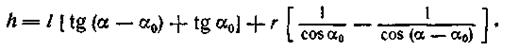
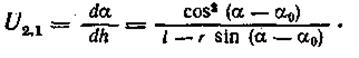






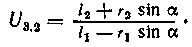
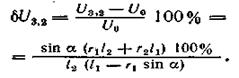


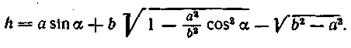
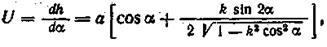
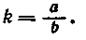

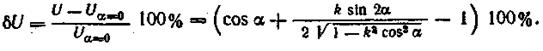
 На рис. 50 показаны кривые изменения δ U в зависимости от а при различных значениях k. Из графика видно, что изменение δ U для кривошипно-шатунных механизмов весьма значительно и достигает 20—25% при угле поворота ведущего звена α = 40°. Поэтому в передаточных механизмах точных приборов изменение передаточного отношения кривошипно-шатунного механизма должно учитываться при выборе чувствительного элемента и расчете шкалы. Если в передаточном механизме прибора передаточное отношение должно быть постоянным, то при использовании кривошипно-шатунного механизма его рабочий угол поворота может быть определен из графика по допустимой величине δU.
На рис. 50 показаны кривые изменения δ U в зависимости от а при различных значениях k. Из графика видно, что изменение δ U для кривошипно-шатунных механизмов весьма значительно и достигает 20—25% при угле поворота ведущего звена α = 40°. Поэтому в передаточных механизмах точных приборов изменение передаточного отношения кривошипно-шатунного механизма должно учитываться при выборе чувствительного элемента и расчете шкалы. Если в передаточном механизме прибора передаточное отношение должно быть постоянным, то при использовании кривошипно-шатунного механизма его рабочий угол поворота может быть определен из графика по допустимой величине δU.




 шатуном — тяга. 7 (размер b), преобразуется в поступательное движение ползушки 6. Последовательно с кривошипно-шатунным механизмом соединены механизмы: синусный 6, 9 и зубчатый 4, преобразующие поступательное перемещение ползушки во вращательное движение стрелки 2 относительно шкалы /. Для обеспечения силового замыкания звеньев механизма служит волосок 3.
шатуном — тяга. 7 (размер b), преобразуется в поступательное движение ползушки 6. Последовательно с кривошипно-шатунным механизмом соединены механизмы: синусный 6, 9 и зубчатый 4, преобразующие поступательное перемещение ползушки во вращательное движение стрелки 2 относительно шкалы /. Для обеспечения силового замыкания звеньев механизма служит волосок 3.
 Если ведущим является рычаг 2 и k =
Если ведущим является рычаг 2 и k =  , то передаточное отношение U 1,2 =
, то передаточное отношение U 1,2 =  =
=  .
. На графике (рис. 52, б) показано изменение передаточного отношения для различных значений k. при k = 1 передаточное отношение постоянно и равно 0,5.
На графике (рис. 52, б) показано изменение передаточного отношения для различных значений k. при k = 1 передаточное отношение постоянно и равно 0,5. и δ = arccos
и δ = arccos  .
.
 Как видно из рис. 55, β = γ + δ, поэтому характеристика
Как видно из рис. 55, β = γ + δ, поэтому характеристика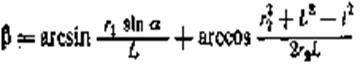 (31)
(31) (из треугольника О'АО).
(из треугольника О'АО).


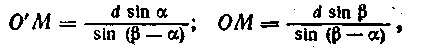


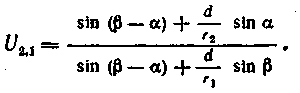 - (32)
- (32) Поводковые механизмы относятся к пространственным механизмам. Их применяют в различных измерительных приборах для преобразования вращательного движения ведущего звена во вращательное движение ведомого звена. Последнее находится под определенным углом к ведущему звену.
Поводковые механизмы относятся к пространственным механизмам. Их применяют в различных измерительных приборах для преобразования вращательного движения ведущего звена во вращательное движение ведомого звена. Последнее находится под определенным углом к ведущему звену.

 По назначению винтовые механизмы разделяют на силовые и кинематические. Силовые механизмы предназначены для значительных нагрузок. Они должны иметь высокий КПД и достаточную прочность элементов передачи — резьбы. Кинематические механизмы применяют для точных перемещений узлов приборов и регулирования взаимного расположения деталей. Кинематические механизмы должны иметь достаточную точность преобразования движения, отсутствие «мертвых» ходов за счет зазоров в резьбах, т. е. минимальные накопленную и циклическую погрешности.
По назначению винтовые механизмы разделяют на силовые и кинематические. Силовые механизмы предназначены для значительных нагрузок. Они должны иметь высокий КПД и достаточную прочность элементов передачи — резьбы. Кинематические механизмы применяют для точных перемещений узлов приборов и регулирования взаимного расположения деталей. Кинематические механизмы должны иметь достаточную точность преобразования движения, отсутствие «мертвых» ходов за счет зазоров в резьбах, т. е. минимальные накопленную и циклическую погрешности.
 d1 — внутренний диаметр резьбы
d1 — внутренний диаметр резьбы  а — угол профиля (для всех метрических резьб а = 60°).
а — угол профиля (для всех метрических резьб а = 60°).
 меру трубы, выраженному в дюймах, например «труба 1/8"». Профиль резьбы представляет собой равнобедренный треугольник с углом при вершине 55°.
меру трубы, выраженному в дюймах, например «труба 1/8"». Профиль резьбы представляет собой равнобедренный треугольник с углом при вершине 55°.


