
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоотдача при вынужденной конвекцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
7.4.1.Теплоотдача в прямолинейных каналах Интенсивность теплоотдачи в прямых гладких каналах при вынужденной конвекции определяется в основном режимом движения теплоносителя. Ламинарный режим. При ламинарном движении необходимо учитывать влияние естественной конвекции. Наличие ее меняет закон распределения скорости в сечении, что сказывается на интенсивности теплообмена. Для определения коэффициента теплоотдачи при ламинарном течении теплоносителя в прямых гладких трубах при (l/d)>50 используется критериальное уравнение М.А. Михеева [6]:
Здесь индекс „ ср“ у критериев обозначает, что в качестве определяющей температуры принята средняя по длине канала температура теплоносителя. Критерий же Prcm определяется для теплоносителя при температуре стенки. Определяющим размером в этом уравнении является эквивалентный диаметр. Отношение Prcp/Prcm в уравнениях (7.14, 7.15) учитывает влияние на теплоотдачу направления теплового потока. Так как величина критерия Прандтля для жидкостей с увеличением температуры уменьшается, то при Тcm>Tm отношение Prcp / Prcm будет больше единицы, в случае Tm> Tcm это отношение меньше единицы. Отсюда при прочих равных условиях теплоотдача интенсивнее в случае направления теплового потока от стенки к теплоносителю. Это явление можно объяснить меньшей толщиной теплового пограничного слоя вследствие влияния температуры на вязкость теплоносителя. Турбулентный режим. При турбулентном режиме движения теплоноситель в канале весьма интенсивно перемешивается, и естественная конвекция не оказывает влияния на теплоотдачу. Для определения среднего коэффициента теплоотдачи при развитом турбулентном движении повсеместно используется критериальное уравнение М.А. Михеева [6].
Для воздуха эта формула упрощается:
Индексы у критериев теплового подобия „ cp“ и „ d “ показывают, что за определяющую температуру принята средняя температура теплоносителя по длине канала, а определяющий размер ─ эквивалентный диаметр канала. Уравнения (7.16) и (7.17) применимы для прямых гладких труб при (l/d)>50 в пределах Re = 1×104... 5×105 и Pr = 0,6... 2500. Для переходного режима (от ламинарного к турбулентному) надежных критериальных уравнений нет. Для определения приближенного коэффициента теплоотдачи в этой области можно использовать уравнение, рекомендованное в [6].
где К определяют из табл. 7.1. Т а б л и ц а 7.1
7.4.2.Теплоотдача на начальном участке канала При вынужденном движении теплоотдача по длине канала неодинакова. Непосредственно у входа в канал коэффициент теплоотдачи имеет максимальное значение, на последующих участках длины он резко убывает, асимптотически приближаясь к некоторому постоянному значению, рис. 7.5а. Такая закономерность объясняется полем скоростей теплоносителя, (см. рис. 7.5 b).
Рис. 7.5 На входе в канал скорость теплоносителя одинакова по всему его сечению, динамический пограничный слой только начинает обозначаться, отсюда максимальное значение теплоотдачи. Далее, по каналу, скорость по сечению изменяется, толщина пограничного слоя растет, а коэффициент теплоотдачи падает. На некотором расстоянии от входа в канал скоростное поле стабилизируется, δд принимает постоянное значение, постоянным становится и коэффициент теплоотдачи α. Участок канала от входа до сечения стабилизации температурного поля теплоносителя называют участкомтепловой стабилизации. Экспериментально установлено, что для горизонтальных каналов длина участка тепловой стабилизации lcm ≈ 50dэкв. Для определения коэффициента теплоотдачи на участке стабилизации используются те же уравнения, но с введением поправочного коэффициента αcm = εl α. Величина поправочного коэффициента εl определена экспериментально в зависимости от длины начального участка канала и значения Re, (табл. 7.2).
Таблица 7.2
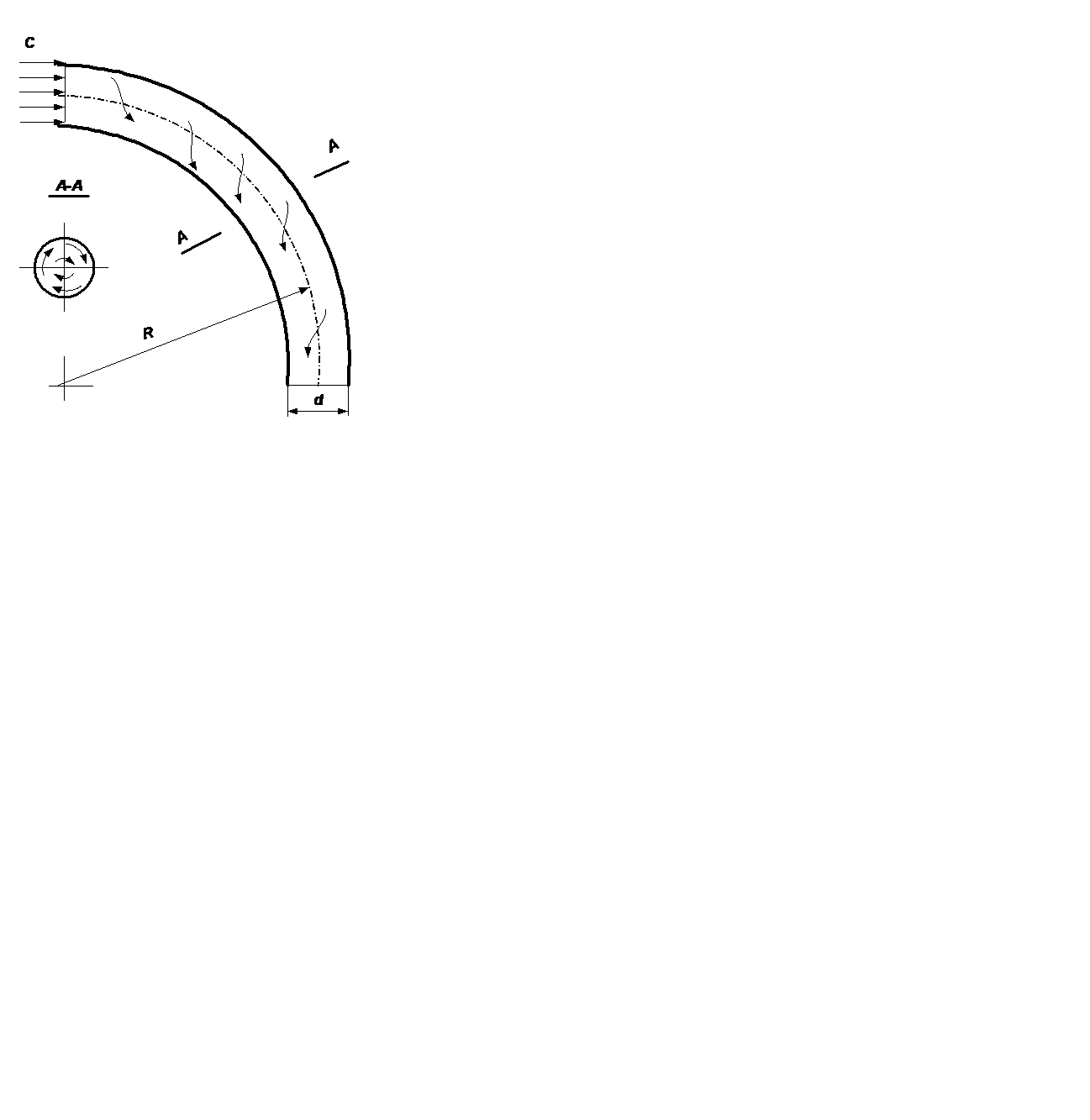
7.4.3. Теплоотдача в изогнутых каналах При движении теплоносителя в изогнутых каналах (отводах, коленах, змеевиках) неизбежно возникает центробежный эффект, характер движения нарушается: поток теплоносителя отжимается к внешней стенке, отчего в поперечном сечении возникает так называемая в т о р и ч н а я ц и р к у-
Это приводит к значительному повышению коэффициента теплоотдачи по сравнению с его значением для прямых каналов. Теплоотдача в таких каналах рассчитывается по формулам для прямолинейных каналов с последующим умножением на поправочный коэффициент
где d – диаметр трубы; R – радиус кривизны канала. Рис. 7.6
7.4.4. Теплообмен потока с преградами При обтекании тел, стоящих на пути движения теплоносителя, форма их поверхности определяет условия формирования пограничного слоя и поэтому существенно влияет на интенсивность теплоотдачи. На рис. 7.7 а показана картина течения при поперечном обтекании цилиндра (трубы). В месте натекания потока на поверхность образуется пограничный слой, толщина которого по мере движения теплоносителя вдоль образующей цилиндра увеличивается. Затем происходит отрыв потока, и образуются вихри. С изменением характера обтекания меняется и коэффициент теплоотдачи. На рис. 7.7 б показано изменение относительного значения коэффициента теплоотдачи по окружности цилиндра. Здесь
а б Рис. 7.7 Если теплоноситель натекает на цилиндр под прямым углом к его оси, то среднее значение коэффициента теплоотдачи можно вычислить с использованием критериального уравнения, [4].
Которое справедливо в пределах 103 < Re < 2 × 105 и 0,6 < Pr < 8 × 103. Другие критериальные уравнения, описывающие конвективный теплообмен при взаимодействии теплоносителя с преградами, приведены в Приложении табл. 13.
7.4.5. Теплоотдача в газоходах Часто теплотехнические задачи состоят в необходимости определения коэффициентов теплоотдачи в каналах различных форм и размеров, например, газоходах котельных установок, в цилиндрах и теплообменниках поршневого компрессора, в коллекторах и глушителях ДВС и т.п. При этом теплоноситель может быть в виде а э р о з о л е й. Аэрозоль – это коллоидная система, состоящая из газовой среды, в которой взвешены твердые или жидкие частицы (дым, туман). Теплоотдачу аэрозолей в прямых гладких каналах можно определить по критериальному уравнению, рекомендованному в работе [12],
где Nua ,d – критерий Нуссельта аэрозоли, Nu г,d – критерий Нуссельта чистого газа;
cm и ρmр – массовая теплоемкость и плотность частиц, соответственно; cг и ρг – массовая теплоемкость и плотность газа, соответственно. Для газоходов в виде коротких каналов при определении критерия Нуссельта чистого газа при Re> 104 можно использовать выражение:
Здесь Nu m,d – среднее по длине канала значение Нуссельта. За определя -ющую температуру принята температура теплоносителя на входе в канал, за определяющий размер – d экв. В криволинейных газоходах интенсивность теплоотдачи возрастает, найденное по уравнению (7.22) значение α нужно умножить на поправочный коэффициент εR (7.19). В сечениях газоходов, где теплоноситель меняет направление течения на угол 90о и более, значение коэффициента теплоотдачи возрастает примерно в 1,8 раза. В некоторых типах газоходов теплоносителю приходится омывать трубчатые теплообменники. Такие теплообменники, как правило, выполняются в виде пучков труб с нормальным расположением к направлению движения теплоносителя. Различают коридорное и шахматное расположение труб в пучке, рис. 7.8. Первый ряд труб в обоих пучках по условиям обтекания близок к одиночной трубе, трубы же последующих рядов находятся в других условиях. Если для шахматного пучка (см.рис.7.8 б) характер обмывания последующих рядов труб мало отличается от труб первого ряда, то для коридорного (см. рис. 7.8 а) эти отличия весьма существенны.
а б Рис. 7.8 В коридорных пучках все трубы второго и последующих рядов находятся в вихревой зоне впереди стоящих труб, причем циркуляция теплоносителя в вихревой зоне слабая, так как поток в основном проходит в продольных зазорах между трубами. Поэтому в коридорных пучках как лобовая, так и кормовая части труб омываются со значительно меньшей интенсивностью, чем те же части одиночной трубы или труб первого ряда. В шахматных пучках характер обтекания глубоко расположенных труб качественно мало отличается от характера обтекания труб первого ряда. Многочисленные исследования теплоотдачи пучков труб показали, что средняя теплоотдача первого и последующих рядов труб различна и определяется первоначальной турбулентностью потока. Начиная с третьего ряда, средняя теплоотдача стабилизируется. Если для третьего ряда теплоотдачу принять за 100 %, то для первого ряда шахматных и коридорных пучков она составит всего лишь 60 %, а для второго ряда - 70 % шахматного и 90 % коридорного пучков. Теплоотдача пучков труб зависит также от расстояния между трубами, которое принято выражать в виде безразмерных характеристик s1/d и s2/d, называемых соответственноо т н о с и т е л ь н ы м п о п е р е ч н ы м и п р о д о л ь н ы мш а г а м и. Согласно [4], при режиме течения теплоносителя, соответствующем Re = 103...105, средний коэффициент теплоотдачи, начиная с третьего ряда пучков труб, может быть найден по уравнению:
где для шахматных пучков К = 0,41, а = 0,6 и для коридорных – К = 0,26, а =0,65. Поправочный коэффициент εs учитывает влияние относительных шагов. Для коридорного пучка ε s = (s2 / d)-0,15; для шахматного при s1/s2 <2 εs = (s1 / d)1/6 и при s1/s2 >2. εs = 1,2. В формуле (7.23) определяющим размером является внешний диаметр труб d. Скорость теплоносителя подсчитывается по самому узкому поперечному сечению ряда пучка. За определяющую температуру принята температура теплоносителя перед соответствующим рядом пучка. Для других режимов течения теплоносителя критериальные уравнения приведены в табл. 14 Приложения.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 423; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.227.73 (0.007 с.) |

 . (7.15)
. (7.15)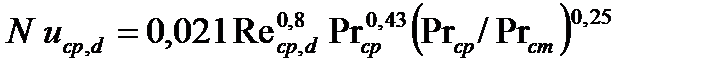 (7.16)
(7.16) (7.17)
(7.17) (7.18)
(7.18)
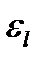 , т.е.
, т.е.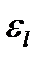
 л я ц и я, рис. 7.6.
л я ц и я, рис. 7.6. . Для змеевиковых труб значение εR определяется по эмпирической формуле:
. Для змеевиковых труб значение εR определяется по эмпирической формуле: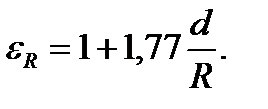 , (7.19)
, (7.19) - местное значение коэффициента теплоотдачи, α - среднее его значение по контуру. Как видно из рисунка, в месте набегания потока на цилиндр (
- местное значение коэффициента теплоотдачи, α - среднее его значение по контуру. Как видно из рисунка, в месте набегания потока на цилиндр ( = 0) коэффициент
= 0) коэффициент  максимален. С увеличением угла теплоотдача резко падает и при
максимален. С увеличением угла теплоотдача резко падает и при  = 90 …100о, т.е. в области отрыва потока от поверхности,
= 90 …100о, т.е. в области отрыва потока от поверхности,  имеет минимальное значение. При
имеет минимальное значение. При  > 120о интенсивность теплоотдачи возрастает вследствие вихреобразований.
> 120о интенсивность теплоотдачи возрастает вследствие вихреобразований.
 , (7.20)
, (7.20) , (7.21)
, (7.21) – объемная доля частиц в газе;
– объемная доля частиц в газе;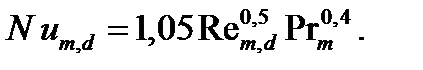 (7.22)
(7.22)
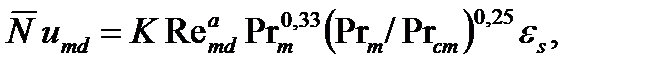 (7.23)
(7.23)


