Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соотношение между теплотой, работой и внутренней энергией.Содержание книги
Поиск на нашем сайте
Для оценки доли теплоты, затраченной на изменение внутренней энергии, в термодинамике при исследовании циклов вводят коэффициент α, которым обозначают отношение α = Долю тепла, расходуемую на совершение работы расширения, обозначают через
Выразив изменение внутренней энергии и теплоту через теплоемкости, получим: α = Таким образом, распределение теплоты между внутренней энергией и работой в процессе можно оценить по известному показателю политропы. В теплотехнике часто используются так называемые и з о п а р а м е т- р и ч е с к и е процессы: изобарный, изохорный, изотермический и адиабатный.
2.3.3. Изобарный процесс Процесс, протекающий при постоянном давлении, называют и з о- б а р н ы м. Уравнение процесса записывается в виде p = const или cn = cp. Из уравнения политропы следует, что для изобарного процесса n = 0. Соотношение параметров в начальном и конечном состояниях процесса устанавливается с использованием уравнений состояния, записанных для этих точек: p1v1 = RT1 и p2v2 = RT2. Поделив одно уравнение на другое, получим:
В изобарном процессе объемы одного и того же количества газа изменяются прямо пропорционально абсолютным температурам. График процесса называется и з о б а р о й. В pv–координатах (рис.2.8) изобара – прямая линия, параллельная оси удельных объемов. В координатах Ts изобара – логарифмическая кривая (рис.2.9), так как она описывается уравнением, полученным из (2.51) при n = 0: si = s1 + cp ln Крутизна изобары в Ts-координатах для каждой температуры определяется тангенсом угла наклона кривой к оси абсцисс, т.е. tg β = Принимая во внимание, что для изобарного процесса справедливы уравнения dq = T ds и dq = cp dT, получим: tg β = Рис. 2.8 Рис. 2.9 Отсюда следует, что с увеличением температуры и уменьшением теплоемкости крутизна изобары растет. Подкасательная к изобаре в любой точке определяет значение истинной теплоемкости cp при температуре T. Все изобары являются эквидистантными кривыми (на рис.2.9 изобары при р, р* и р**), так как при одной и той же температуре они имеют одинаковые угловые коэффициенты. Кроме того, расстояние между двумя изобарами вдоль оси абсцисс при разных температурах одинаково. Так при температуре T1 отрезок ce между изобарами р* и р** определяется выражением:
Аналогично найдем отрезок d f межу теми же изобарами при температуре Т2.
В итоге получили Изменение внутренней энергии запишем через теплоемкость при постоянном давлении, используя для этой цели уравнение Майера: ∆u = (cp – R) (T2 – T1). Изменение энтальпии в процессе вычисляется как ∆i = cp(T2 - T1). Приращение энтропии можно записать и через cp, и через cv: s2 – s1= cp ln (T2/T1) и s2 – s1 = cv ln (T2/T1) + R ln (v2 /v1). Работа расширения выражается следующим образом: l расш = При изменении температуры на один градус работа расширения численно равна величине газовой постоянной. Техническая работа будет равна нулю, так как dp = 0: l тех = - Количество теплоты, сообщаемое газу в изобарном процессе, вычисляется по уравнению: q = cp (Т2 – Т1) = i2 – i1. Часть сообщенной теплоты идет на изменение внутренней энергии, а другая часть – на работу расширения. α = 2.3.4. Изохорный процесс Процесс, протекающий при постоянном объеме, называется и з о х о р н ы м. Уравнение процесса записывается в виде v = const или cn = cv. Показатель политропы для изохорного процесса получим из уравнения политропы, если раскроем его относительно удельного объема: v = Из этого следует, что удельный объем может быть постоянным только при показателе политропы, равном n= ±∞. Из уравнения состояния при v=const получим связь между параметрами в конечных точках процесса:
Это значит, что при постоянном объеме давление газа изменяется прямо пропорционально изменению абсолютной температуры. График процесса называется и з о х о р о й. В pv –координатах (рис.2.10) изохора – прямая линия, параллельная оси давлений. В координатах Ts изохора (рис.2.11) – логарифмическая кривая, так как текущие значения энтропии и температуры связаны уравнением: si - s1 = Как и в изобарном процессе, крутизна изохоры в Ts-координатах определяется угловым коэффициентом tg γ = T/cv. Из последнего выражения следует, что крутизна изохоры растет с увеличением температуры и уменьшением теплоемкости. Сравнение угловых коэффициентов изохоры и изобары показывает, что при одной и той же температуре изохора проходит круче, так как cp>cv.
Рис. 2.10 Рис. 2.11 Изохоры, так же как и изобары, эквидистанты (рис.2.11). Как и в изобарном процессе, можно показать, что ac = bd. Для вычисления изменения внутренней энергии, энтальпии и энтропии в процессе от начального до конечного состояний используются уравнения: ∆u = cv(Т2 – Т1), ∆i = cp(Т2 –Т1) и Работа расширения в изохорном процессе равна нулю. Техническая работа определится по формуле: lтех= - Так как lрасш = 0, то из первого закона термодинамики следует, что все подведенное тепло расходуется на изменение внутренней энергии: q = u2 – u1= cv (T2 – T1). Значения α и ξ для изохорного процесса будут равны: α =
2.3.5. Изотермический процесс Процесс, протекающий при постоянной температуре, называется и з о т е р м и ч е с к и м. Уравнение процесса записывается в виде Т = const или pv = const. (2.59) Следовательно, показатель процесса n = 1, а теплоемкость сT = ± Отсюда же: отношение удельных объемов обратно пропорционально отношению давлений, т.е.
График процесса, построенный по уравнению (2.59), называют и з о- т е р м о й. В pv– координатах (рис.2.12) изотерма – равнобочная гипербола. В координатах Ts изотерма – прямая линия параллельная оси абсцисс, рис.2.13.. Рис. 2.12 Рис. 2.13 Изменения внутренней энергии и энтальпии в процессе равны нулю, т.е. du = cvdT = 0 и di =cpdT = 0. Изменения энтропии в изотермическом процессе можно выразить через удельный объем и через давление:. ds = Интегрируя данное выражение от первого состояния до второго, получим: ∆ѕ=ѕ2 –ѕ1=R ln Для изотермического процесса работа расширения равна технической работе: lрасш = и lтех = - Теплота, участвующая в процессе q = T (s2 – s1) =RT ln В данном процессе все тепло, подведенное к газу, идет на совершение работы расширения: Коэффициент α для изотермического процесса равен нулю, значение ξ - единице, т.е. α =
2.3.6. Адиабатный процесс А д и а б а т н ы м называют процесс изменения состояния системы, происходящий без теплообмена с окружающей средой. В адиабатном процессе dq = 0, следовательно, теплоемкость сq = 0. Для вывода уравнения адиабаты используем выражения первого закона термодинамики (1.17) и (1.18) при dq = 0: cp dT –v dp = 0 и cv dT + p dv = 0 Разделим первое уравнение на второе:
сократив на dT, разделив переменные и обозначив cp/cv =к, будем иметь: к Проинтегрировав полученное уравнение от начального до конечного состояния процесса, получим: к ln или p1 v1к = p2 v2к. На основании этого запишем уравнение адиабаты: p vк = const. (2.60) При адиабатном процессе произведение давления на удельный объем в степени к есть величина постоянная. Кривую, построенную по уравнению (2.60), называют а д и а б а т о й, а величину к, являющуюся отношением теплоемкостей cp и cv – п о к а з а т е л е м а д и а б а т ы. Уравнение адиабатного процесса аналогично политропному, разница лишь в том, что здесь вместо показателя политропы п имеем показатель адиабаты к. Поэтому все последующие соотношения для адиабатного процесса получим из политропных, заменив п на к. Так, связь между параметрами в адиабатном процессе имеет вид:
Адиабата в pv -координатах представляет собой неравнобочную гиперболу, рис.2.14. Она круче изотермы, так как к >1. В Ts-координатах адиабата изображается вертикальной прямой, рис. 2.15, потому что при q = 0 изменения энтропии нет, т.е. ∆s = 0. В этом случае адиабатный процесс можно называть и з о э н р о п н ы м процессом Рис. 2.14 Рис. 2.15 Изменение энтальпии и внутренней энергии определяются по уравнениям: ∆i =cp (T2 –T1) и ∆u = cv (T2 – T1). Заменив в уравнении (2.52) и (2.53) п на к, получим работу расширения и техническую работу: lрасш = Отсюда следует, что в адиабатном процессе техническая работа в к раз больше величины работы расширения. Поскольку теплота в адиабатном процессе равна нулю, то работа расширения совершается только за счет изменения внутренней энергии рабочего тела.
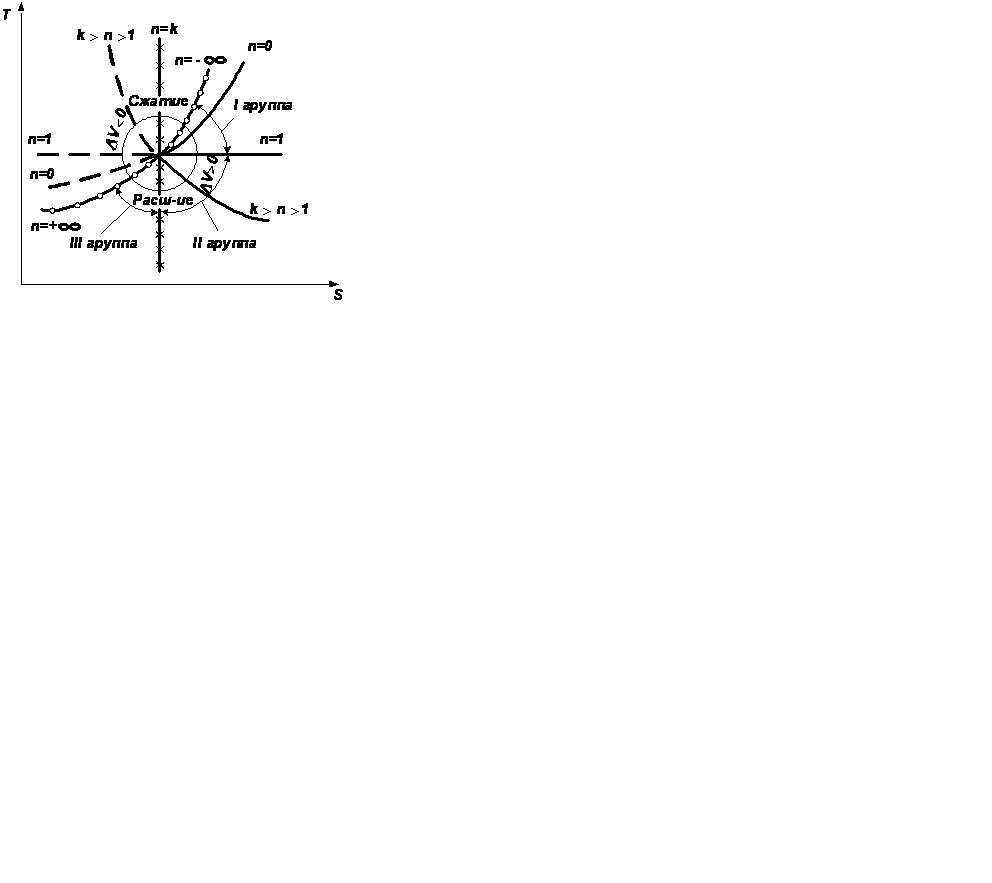
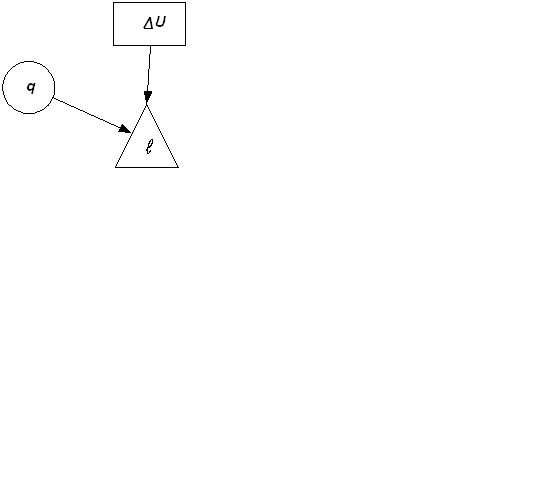
2.3.7. Характерные группы политропных процессов В зависимости от энергообмена системы с окружающей средой поли- тропные процессы расширения можно разбить на три характерные группы: I группа – с показателем процесса п от -∞ до 1; II группа – с показателем процесса п от 1 до к; III группа – с показателем процесса п от к до +∞. Распределение процессов по группам в pv и Ts – координатах показано на рис.2.16.(а) и рис.2.16 (б), соответственно. Процессы, лежащие выше изотермы, протекают с увеличением внутренней энергии, ниже – с ее уменьшением. К процессам, расположенным над адиабатой, теплота подводится, под адиабатой – отводится. Процессы расширения лежат справа от изохоры, сжатия – слева. Для первой группы характерным является то, что все процессы расширения идут с подводом тепла и увеличением внутренней энергии. Связь между теплотой, работой и внутренней энергией можно представить схематически, рис.2.17. В первой группе процессов (а) вся теплота идет на совершение работы расширения и увеличение внутренней энергии.
а) б) Рис.2.16
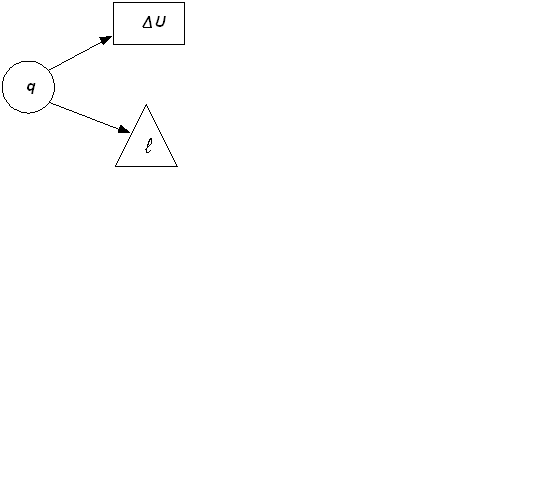
а) б) в) Рис. 2.17 Во второй группе (б) теплота тоже подводится, но внутренняя энергия уменьшается. В этом случае работа расширения совершается за счет подведенного тепла и уменьшения внутренней энергии. Третью группу (в) отличает то, что все процессы расширения идут с отводом теплоты и уменьшением внутренней энергии. Работа процессов этой группы производится только за счет уменьшения внутренней энергии. Кроме того, внутренняя энергия дополнительно еще уменьшается вследствие отвода теплоты от системы.
2.3.8. Диаграммы состояния Изображение процессов в координатах, по осям которых выбраны те или иные параметры. позволяет построить для рабочих тел характерные диаграммы состояния, широко использующиеся при исследовании термодинамических процессов и циклов. Рассмотрим некоторые из них. Диаграмма состояния в pv – координатах представляет собой сетку из изобар и изохор, на которую наложены изотермы. По этой диаграмме можно быстро определить в любом состоянии термодинамические параметры рабочего тела, для которого она построена. Однако pv-диаграмма дает недостаточно полную информацию о рабочем теле и процессах изменения его состояния. Диаграмма состояния в Ts – координатах позволяет непосредственно определить большее число параметров, так как на поле графика, состоящего из сетки изотерм и изоэнтроп, наносятся уже два вида изопараметрических процессов: изохоры и изобары. По этой диаграмме для любого состояния можно определить T, p, v, s, а также cp и cv. Некоторым недостатком рассмотренных диаграмм является то, что при определении количества работы (в pv – диаграмме) и количества теплоты (в Ts – диаграмме) приходится измерять соответствующие площади. В технических расчетах чаще используется диаграмма, построенная в is-координатах. Достоинством такой диаграммы является то, что на ней работа и теплота процессов изображаются отрезками линий. При построении диаграммы по оси ординат откладывается энтальпия, а по оси абсцисс – энтропия. На рис. 2.18 представлена is – диаграмма водяного пара. На поле графика из изоэнтальп и изоэнтроп наносятся изобары, изохоры и изотермы. Имея is – диаграмму, по двум известным параметрам можно просто найти остальные параметры состояния рабочего тела. Так, например, по p и T непосредственно определяются i, s, v, cp, cv и вычисляются R, к, u. В адиабатном процессе расширения от состояния 1 до состояния 2 отрезок оси ординат В холодильной технике, как правило, используются диаграммы состояния хладагентов в координатах ln p – i. Для фреона R–22 диаграмма состояния представлена в Приложении табл. 16.
Рис. 2.18
Глава 3 ПАР И ВЛАЖНЫЙ ВОЗДУХ
3.1. Парообразование жидкостей 3.1.1. Особенности фазовых переходов Во многих технических системах нашли широкое распространение рабочие тела в виде пара различных веществ: воды, аммиака, углекислоты, фреона. Кроме того, часто используются как газообразные, так и сжиженные кислород, азот и др. газы. Как получение пара из жидкости, так и получение жидкого вещества из газа осуществляется в результате фазовых переходов. Известны четыре агрегатных состояний вещества: твердая, жидкая, газообразная фазы и плазма. Каждая фаза представляет собой однородную систему с одинаковыми физическими свойствами во всех ее частях. Характерной особенностью агрегатного состояния вещетва является наличие гранниц, отделяющих данную фазу от соприкасающихся с нею других фаз. При определенных условиях вещество может переходить из одной фазы в другую. Процесс перехода вещества из твердой фазы в жидкую носит название п л а в л е н и я. Обратный переход именуют к р и с т а л- л и з а ц и е й. В некоторых условиях твердое вещество может переходить сразу в газообразную фазу, минуя жидкое состояние. Процесс перехода твердой фазы в газообразную называют с у б л и - м а ц ие й, а обратный процесс – д е с у б л и м а ц и е й.
Процесс перехода вещества из жидкого состояния в газообразное именуют п а р о о б р а з о в а н и е м, из газообразного в жидкое – к о н д е н с а ц и е й. Различают фазовые переходы 1-го и 2-го родов. К фазовым переходам 1-го рода относят превращения, сопровождающиеся поглощением или выделением теплоты r и скачкообразным изменением удельного объема v, т.е. dq В теплоэнергетических установках чаще используются вещества, которым присущи фазовые переходы 1-го рода. Граница между двумя фазами при любых фазовых переходах представляет собой поверхность равновесия фаз, на которой градиенты давлений и температур равны нулю. Пересечение поверхности равновесия плоскостью, соответствующей фиксированному значению одного из параметров состояния, дает кривую равновесия, изображенную в координатах других параметров. Так, например, кривые равновесия воды можно представить в координатах pT в виде уравнения:
где r - теплота фазового перехода. Начало координат задается таким, что на поле pT - диаграммы можно разместить состояния твердой, жидкой и газообразной фаз какого-либо вещества. Равновесное состояние этого вещества, а также равновесные состояния фазовых переходов изображаются точками. Точка, в которой находятся в равновесном состоянии три фазы однородного вещества, называется т р о й н о й т о ч к о й. Тройная точка является началом кривых функций p=f(T) для фазовых переходов: твердое вещество – жидкость, жидкость – пар, твердое вещество - пар. Характер этих кривых определяется выражением (3.1). На рис.3.1 представлена качественная pT – диаграмма воды. Тройная точка воды A имеет давление p = 0,0061 бар (610 Па) и температуру t = 0,01о С. При переходе воды из жидкого состояния в газообразное удельный объем ее возрастает (
твердом состоянии (на рис.3.1 точка 1) Рис. 3.1 нагревать при постоянном давлении p1, то будем иметь следующие процессы: 1-b – нагрев до температуры плавления и переход в жидкую фазу; b-c – нагрев жидкости до температуры кипения и переход в пар; c-2 – перегрев пара до температуры T2. Если взять состояние 3 с давлением p3, то при нагреве твердого вещества получим процессы: 3-d – нагрев твердого вещества до температуры сублимации; d-4 – сублимация и перегрев пара до температуры T4. Кривая парообразования AC заканчивается критической точкой Kp. При температуре, равной критической, взаимные превращения пара и жидкости происходят без поглощения или отвода тепла и без скачкообразного изменения плотности.
3.1.2. Пар и его характеристики Под паром понимают газообразное состояние вещества в условиях, когда газовая фаза может находиться в равновесии с жидкой (твердой) фазой того же вещества. Для получения пара используется процесс парообразования, хотя пар может быть получен и в процессе сублимации. Парообразование является следствием испарения и кипения. Испарение происходит только со свободной поверхности жидкости. Оно протекает при любой температуре и осуществляется за счет покидания жидкости молекулами, обладающими кинетической энергией, достаточной для преодоления поверхностного натяжения и перехода в пространство над жидкостью. Интенсивность испарения зависит от температуры жидкости и от ее природы. Процесс кипения заключается в том, что при определенной температуре внутри жидкости образуются пузырьки пара. При испарении жидкости внутрь пузырька его размеры растут. Пузырьки, всплывая, выносят пар в окружающую жидкость среду. При интенсивном кипении суммарная поверхность пузырьков может существенно превосходить свободную поверхность жидкости. В этом случае парообразование будет идти в основном за счет кипения. При парообразовании жидкости в закрытом пространстве одновременно протекает процесс конденсации. При определенных условиях наступит равновесие между жидкостью и паром. Это значит, что при отсутствии внешнего воздействия количественные соотношения между жидкой и газообразной фазами сохраняются неограниченное время. Газообразную фазу, находящуюся в равновесии с жидкой фазой, называют сухим н а с ы щ е н н ы м п а р о м. Из условий равновесия давление сухого насыщенного пара (обозначим его pн) равно давлению фазового перехода: pн = ps. Характерной особенностью процесса кипения является то, что при заданном давлении жидкость закипает при достижении вполне определенной температуры, и эта температура остается неизменной до полного выкипания жидкости. С другой стороны, экспериментально было установлено, что такая связь справедлива только до определенных значений давления и температуры. Так, с увеличением давления при достижении вполне определенной температуры жидкость во всем объеме превращается в пар, и никаким повышением давления нельзя остановить этот процесс. Для примера в табл.3.1 даны приближенные значения температур кипения воды при различных давлениях, а в Приложении табл. 8 приведены физические характеристики воды на линии насыщения. Т а б л и ц а 3.1
Значения температуры и давления, при которых вещество может существовать в двух фазах - жидком и газообразном, называют к р и т и ч е с- к и м и и обозначают tкр и pкр. Для некоторых жидкостей критические параметры приведены в табл. 3.2. Т а б л и ц а 3.2
В сухом насыщенном паре при определенных условиях над поверхностью испарения могут образовываться мельчайшие капельки сконденсированной жидкости. Механическая смесь сухого насыщенного пара и мельчайших капелек жидкости называется в л а ж н ы м паром. Массовая доля сухого пара во влажном называется с т е п е н ь с у х о с т и. Обозначают степень сухости через x и вычисляют как, x = mc /m, где mc – масса сухого пара; m – масса влажного пара. Пар, температура которого выше температуры сухого насыщенного пара при том же давлении, называется п е р е г р е т ы м. Процессы нагрева и парообразования многих жидкостей в теплотехнической справочной литературе представлены в виде диаграмм в различных системах координат (pv, Ts, is, pi). На рис.3.2 представлены качественные диаграммы процессов нагрева
Рис. 3.2
Влажный воздух 3.2.1. Параметры влажного воздуха Воздух представляет собой смесь газов N2, O2, CO2, H2, Ar и H2O, причем относительное содержание всех составляющих смеси, кроме водяного пара, весьма стабильно. Физические свойства сухого воздуха приведены в Приложении табл. 3. Воздух, в котором водяные пары отсутствуют, называетс я с у х им. Смесь водяного пара и сухого воздуха называют в л а ж н ы м воздухом. Поскольку в обычных условиях состав сухого воздуха практически не изменяется, то его можно рассматривать как идеальный газ, для которого μ = 29 кг/моль, R = 287 Дж/(кг·К), к = 1,4. Водяной пар в обычных условиях также представляет собой идеальный газ, имеющий μ=18 кг/моль, R = 462 Дж/(кг·К), к =1,33. В этом случае влажный воздух допустимо рассматривать как смесь двух идеальных газов. Используя закон Дальтона для влажного воздуха, можем записать: p = pc + pп, где pc и pп – парциальные давления сухого воздуха и пара соответственно. Абсолютная влажность Количество пара во влажном воздухе оценивают а б с о л ю т н о й влажностью. Под а б с о л ю т н о й влажностью понимают массу водяного пара в 1м3 влажного воздуха. Из определения следует, что абсолютная влажность – это плотность пара во влажном воздухе, т.е.
Абсолютная влажность при данной температуре будет максимальной, если пар насыщенный. Максимальная влажность обозначается Относительная влажность Отношение действительного значения абсолютной влажности к максимально возможному ее значению при той же температуре называется о т н о с и т е л ь н о й влажностью. Обозначают относительную влажность φ:
Как правило, относительную влажность выражают в процентах, тогда
Для сухого воздуха φ = 0%, влажный насыщенный воздух имеет φ = 100%. Увеличение относительной влажности воздуха происходит за счет добавления в него количества водяного пара. В тоже время, если охлаждать влажный воздух при неизменном парциальном давлении водяного пара, то φ будет увеличиваться вплоть до φ = 100%. Температуру, при которой достигается состояние насыщения влаж- ного воздуха, называют т е м п е р а т у р о й т о ч к и р о с ы и обозначают tр. При температуре ниже tр воздух будет оставаться насыщенным, избыточная же влага выпадает из влажного воздуха в виде капель воды или тумана. Это свойство положено в основу принципа определения tр прибором, называемым гигрометром. При обработке влажного воздуха (подогрев, охлаждение) количество сухого воздуха в нем не изменяется, поэтому целесообразно все удельные величины относить к 1 кг сухого воздуха. Массу водяного пара, приходящуюся на 1 кг сухого воздуха, называютют в л а г о с о д е р ж а н и е м. Обозначают влагосодержание через d, измеряют в г/кг. Из определения следует:
При допущении, что водяной пар и сухой воздух являются идеальными газами, можно записать: pп Vп = mпRпТп и pс Vc = mcRcTс. Почленно разделим их и, учитывая особенности газовых смесей (пар и сухой воздух занимают один и тот же объем и имеют одинаковую температуру), т.е. Vп = Vc и Tп = Тс), получим:
Из уравнения (3.5) следует, что влагосодержание при заданном барометрическом давлении (рбар) зависит только от парциального давления водяного пара. В выражение (3.5) можно ввести значение относительной влажности φ: так, с учетом (3.3)
Из уравнения (3.5) определим парциальное давление водяного пара во влажном воздухе через влагосодержание:
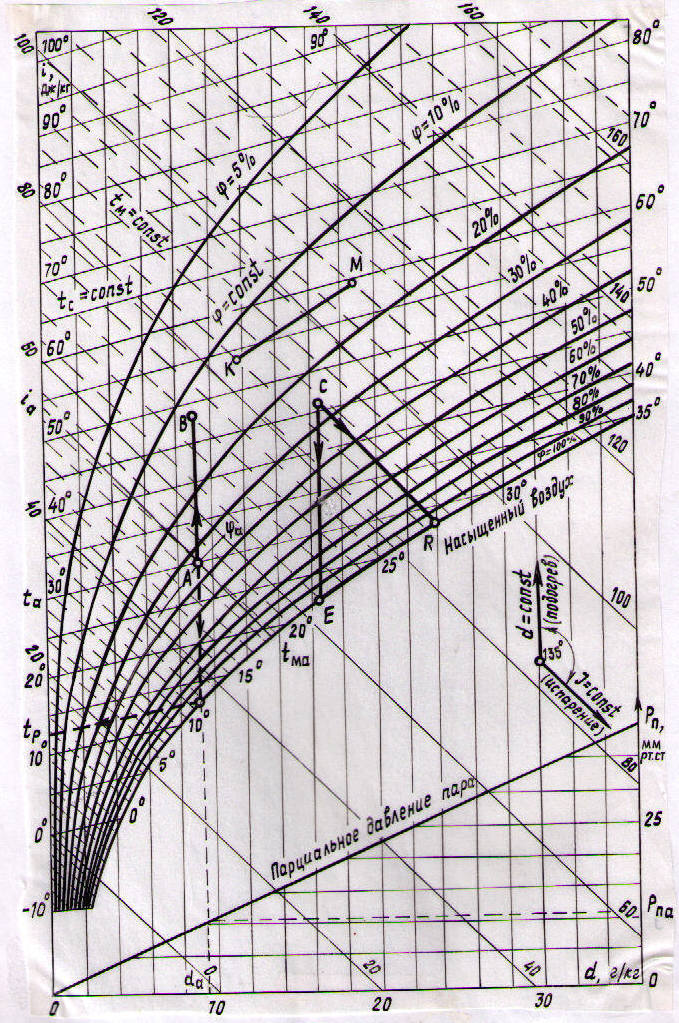
3.2.2. Диаграмма id влажного воздуха Определение параметров влажного воздуха и расчет процессов тепло- и массообмена значительно упрощается при использовании id – диаграммы, которая была предложена в 1918 г Л.К.Рамзиным. Диаграмма (рис. 3.3) построена для барометрического давления 745 мм рт. ст., т.е. 99,3 кПа (среднее годовое давление в Центральной части России), но ею можно пользоваться и при других барометрических давлениях в пределах допустимой точности. При построении диаграммы по оси ординат отложена удельная энтальпия сухого воздуха – i, а по оси абсцисс влагосодержании – d. С целью расширения наиболее используемой для расчетов области, соответствующей насыщенному влажному воздуху, угол между осями выбран равным 1350. Горизонтально проведена вспомогательная ось, на которую спроецированы значения влагосодержания с наклонной оси. Хотя ось абсцисс на диаграмму обычно не наносится, изоэнтальпы идут параллельно ей, поэтому они на диаграмме изображаются наклонными прямыми. Линии d = const проведены параллельно оси ординат. Значения d = const и i = const образуют координатную сетку, на которую наносятся линии постоянных температур (изотермы) и кривые линии относительной влажности (φ=const). Для построения изотерм необходимо выразить энтальпию через влагосодержание. Энтальпия влажного воздуха на основании условия аддитивности выразится как I = Ic + Iп. Поделим величины данного уравнения на массу сухого воздуха, получим: i = ic + Если второе слагаемое умножить и разделить на массу пара, то будем иметь:
Отсчитывая энтальпию от 00С, выражение (3.8) можно записать: i = cpct + d (r0 + cpп t), (3.9) где cpc и cpп – массовые теплоемкости сухого воздуха и пара; r0 – теплота фазового перехода воды в пар при 00С; t – текущее значение температуры. При допущении, что теплоемкости сухого воздуха и пара в диапазоне измеряемых температур постоянны, для фиксированного t уравнение (3.9) представляет линейную зависимость i от d. Следовательно, изотермы в координатах i d будут прямыми линиями. Используя выражение (3.6) и табличные зависимости давления насыщенного пара от температуры pн = f(t), несложно построить кривые относительной влажности. Так, при построении кривой для конкретного φ выбирают несколько значений температур, из таблиц для них определяют pн и по (3.6) вычисляют d. Соединив точки с координатами ti,, di линией, получим кривую φ = const. Линии (φ = const) имеют вид расходящихся кривых, которые претерпевают излом при t = 99,4 0С (температура кипения воды при давлении 745 мм рт. ст), и дальше идут вертикально. Кривая φ=100% делит площадь диаграммы на две части. Выше кривой располагается область влажного воздуха с ненасыщенным паром, а ниже – область влажного воздуха с насыщенным и частично – с конденсированным паром. Изотермы, соответствующие температурам адиабатного насыщения воздуха (tм), на диаграмме проходят под небольшим углом к изоэнтальпам и изображены пунктирными линиями. Они измеряются "мокрым" термометром и обозначаются tм. На кривой φ = 100 % в одной точке пересекаются изотермы сухого и мокрого термометров. В нижней части диаграммы по уравнению (3.7) построена зависимость рп= f(d) для рбар = 745 мм рт ст. По id-диаграмме, зная два любых параметра, можно определит все остальные параметры влажного воздуха. Так, например, для состояния A (см рис. 3.6) имеем ta, ia, φa, da, pпа, tp. Значения температуры ta, энтальпии ia и влагосодержания da есть проекция точки А на оси i, d и t. Величина относительной влажности характеризуется значением на кривой, проходящей через данное состояние.
Рис. 3.3
Для определения температуры точки росы необходимо точку A спроецировать на кривую φ = 100%. Изотерма, проходящая через эту проекцию, дает значение tp. Давление пара определяется по влагосодержанию da и линией pп = f(d). При нагревании воздуха его влагосодержание не изменяется (d=const), а энтальпия возрастает, поэтому процесс нагрева на id-диаграмме изображается вертикальной прямой AB. Процесс охлаждения воздуха также происходит при d=const; энтальпия уменьшается (линия CE), а относительная влажность возрастает вплоть до точки росы, являющейся пересечением прямой охлаждения CE с кривой φ = 100 %. В процессе сушки материала воздух увлажняется. Если при этом теплота, истраченная на испарение влаги, берется из воздуха, то этот процесс приближенно (без учета энтальпии воды) считают изоэнтальпным, так как израсходованная теплота снова возвращается воздуху вместе
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 258; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.165.68 (0.011 с.) |

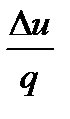 . (2.54)
. (2.54)
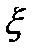 , тогда
, тогда или
или  . (2.55)
. (2.55)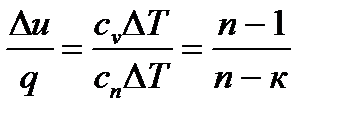 и
и  .
.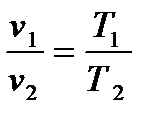 .
. . (2.56)
. (2.56)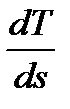 ..
..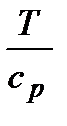 . (2.57)
. (2.57)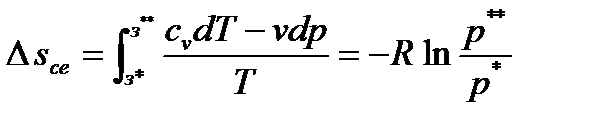 .
.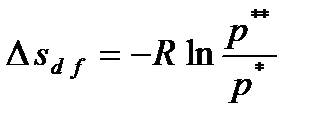 .
.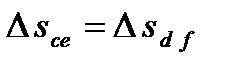 или c e = d f.
или c e = d f.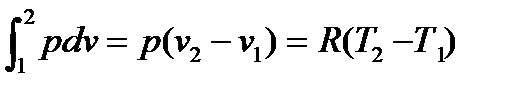 .
.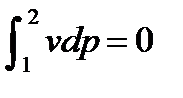 .
. ,
, 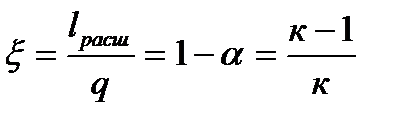 .
.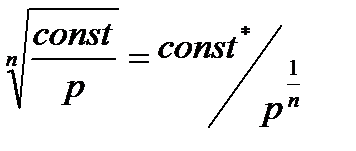 .
. .
. . (2.58)
. (2.58) .
. .
.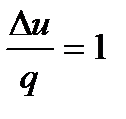 и ξ =1 – α = 0.
и ξ =1 – α = 0.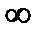 .
.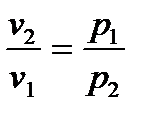 .
. .
. ..
..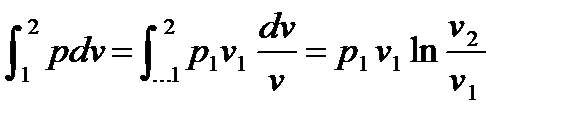 = RT1ln
= RT1ln 

 = RT ln
= RT ln 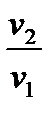 .
.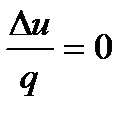 и ξ = 1 – α = 1.
и ξ = 1 – α = 1.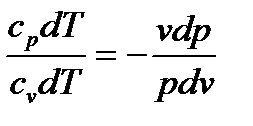 ,
,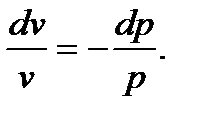

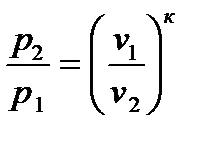 или
или 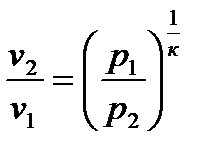 ;
;
 ;
;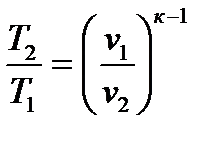 или
или 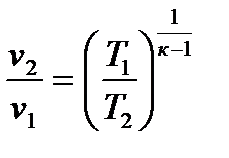
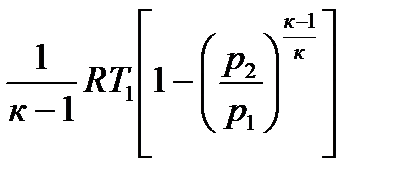 и lтех =
и lтех = 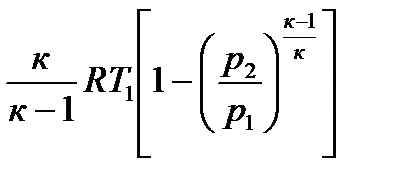 ..
..

 i1 - i2 представляет работу техническую, а в изотермном процессе
i1 - i2 представляет работу техническую, а в изотермном процессе  s = s2 – s1 – эквивалентна теплоте, подведенной в процессе расширения.
s = s2 – s1 – эквивалентна теплоте, подведенной в процессе расширения.
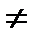 0; r
0; r  и dv
и dv 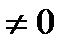 . К фазовым переходам 2-го рода относят превращения при dq =0 и dv =0. В этом случае происходит скачкообразное изменение теплоемкости.
. К фазовым переходам 2-го рода относят превращения при dq =0 и dv =0. В этом случае происходит скачкообразное изменение теплоемкости.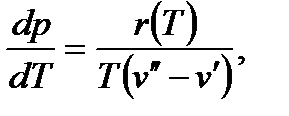 (3.1)
(3.1)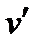 и
и 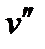 – удельные объемы вещества в начале и конце фазового перехода соответственно;
– удельные объемы вещества в начале и конце фазового перехода соответственно; >
> 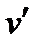 ), а теплота фазового перехода имеет положительное значение (r > 0); тогда из уравнения (3.1) следует, что с увеличением давления температура фазового перехода будет расти (кривая AC) Неравенство
), а теплота фазового перехода имеет положительное значение (r > 0); тогда из уравнения (3.1) следует, что с увеличением давления температура фазового перехода будет расти (кривая AC) Неравенство  >
> 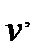 справедливо и при сублимации льда в пар, поэтому с
справедливо и при сублимации льда в пар, поэтому с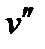 >
>  , следовательно, dp/dT>0. Это значит, что давление плавления с увеличени-
ем температуры растет. Однако удельный объем воды при плавлении льда имеет меньшее значение (
, следовательно, dp/dT>0. Это значит, что давление плавления с увеличени-
ем температуры растет. Однако удельный объем воды при плавлении льда имеет меньшее значение ( <
<  ), и поэтому dp/dT<0, т.е. с увеличением давления температура плавления уменьшается (линия AB). Если вещество в
), и поэтому dp/dT<0, т.е. с увеличением давления температура плавления уменьшается (линия AB). Если вещество в
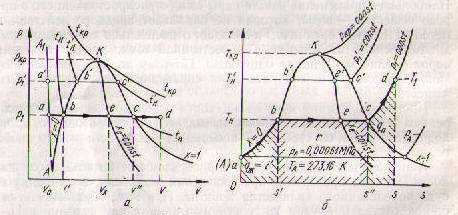 и парообразования воды в pv (а) и Ts (б) – координатах. На этих диаграммах стрелками показан изобарный процесс парообразования: ab – нагрев жидкости до температуры кипения; bc –испарение жидкости; cd – перегрев пара. Точка e позволят описать состояние влажного пара, а точка d – перегретого пара. Точка К определяет критические температуру и давление. В Ts –координатах заштрихованные площади эквивалентны теплоте, потребного для нагрева жидкости до температуры кипения qж; фазового перехода r,перегрева пара qп.
и парообразования воды в pv (а) и Ts (б) – координатах. На этих диаграммах стрелками показан изобарный процесс парообразования: ab – нагрев жидкости до температуры кипения; bc –испарение жидкости; cd – перегрев пара. Точка e позволят описать состояние влажного пара, а точка d – перегретого пара. Точка К определяет критические температуру и давление. В Ts –координатах заштрихованные площади эквивалентны теплоте, потребного для нагрева жидкости до температуры кипения qж; фазового перехода r,перегрева пара qп.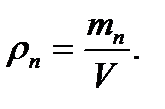 (3.2)
(3.2)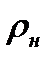 .
.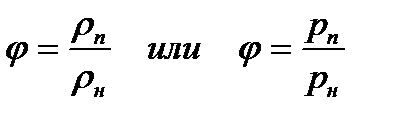 (3.3)
(3.3) ∙ 100, % и
∙ 100, % и 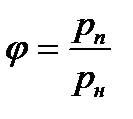 ∙ 100, %.
∙ 100, %.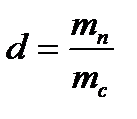 . (3.4)
. (3.4) (3.5)
(3.5) . (3.6)
. (3.6)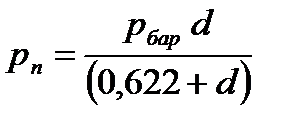 . (3.7)
. (3.7) .
.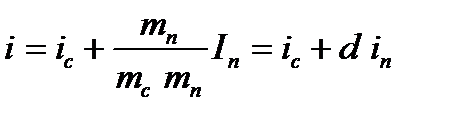 (3.8)
(3.8)