Влияние несимметрии ротора синхронной машины на переходный процесс при нарушении симметрии трехфазной цепи.
Содержание книги
- Поисковое оборудование. Дефектоискатели. Трассодефектоискатели и трассоискатели.
- Система для локализации мест повреждений на кабельных линиях. Установка для прожига места повреждения силовых кабелей.
- Генераторы электростанций. Синхронные генераторы.
- Способы возбуждения синхронных генераторов
- Генераторы электростанций. Характеристики генераторов, работающих на автономную сеть.
- Генераторы электростанций. Включение генераторов на параллельную работу с сетью постоянного напряжения и постоянно частоты.
- Генераторы электростанций. Статическая устойчивость работы генераторов при работе параллельно с сетью бесконечной мощности.
- Основное электрическое оборудование электрических станций. Коммутационные и защитные аппараты высокого напряжения.
- Электрические схемы электростанций и подстанций. Схемы, применяемые на генераторном напряжении.
- Электрические схемы электростанций и подстанций. Схемы, применяемые на высшем и среднем напряжениях.
- Электрические схемы электростанций и подстанций. Типовая сетка схем распределительных устройств
- Электрические схемы электростанций и подстанций. Структурные схемы электрических станций и подстанций
- Электрические схемы электростанций и подстанций. Электроснабжение собственных нужд электростанций и подстанций
- Мощность ГЭС и выработка энергии
- Нетрадиционные источники энергии. Солнечная энергетика.
- Нетрадиционные источники энергии. Ветроэнергетика.
- Устройства и функционирование тэц. Раздельная и комбинированная выработка электроэнергии и тепла. Показатели качества работы тэс
- Устройство и функционирование аэс. Технологические схемы производства электроэнергии на аэс.
- Схемотехника. Регулируемые источники питания, определение, классификация, потенциометр и схема Дарлингтона.
- Схемотехника. Ступенчатые регуляторы.
- Схемотехника. Стабилизаторы напряжения.
- Схемотехника. Согласование сопротивлений, тепловой шум.
- Схемотехника. Усилители на высоких частотах
- Причины возникновения переходных процессов в электроэнергетических системах.
- Выбор выключателей по отключающей способности.
- Влияние несимметрии ротора синхронной машины на переходный процесс при нарушении симметрии трехфазной цепи.
- Особенности распространения токов нулевой последовательности по воздушным линиям электропередач.
- Особенности простого замыкания на землю в распределительных сетях.
- Влияние изменения параметров проводников на значение тока КЗ.
- Расчетов тока КЗ в установках напряжением до 1000в.
- Статическая и динамическая устойчивость системы.
- Критерии устойчивости и избыточная мощность.
- Критерии устойчивости асинхронного двигателя.
- Критерии динамической устойчивости электрической системы.
- Суть метода последовательных интервалов при определении времени отключения.
- Запас устойчивости электрической системы по напряжению.
- Запас устойчивости электропередачи.
- Схемы замещения линии электропередачи.
- Схемы замещения синхронной машины.
- Как можно получить расчетом и экспериментом статические характеристики комплексной нагрузки.
- Статические характеристики асинхронного двигателя. Понятие критического скольжения, момента, мощности. «Опрокидывание» асинхронного двигателя.
- Динамические характеристики асинхронного двигателя.
- Характеристики синхронной нагрузки.
- Выбор токов и времени срабатывания максимальной токовой защиты.
- Токовые защиты с измерительными органами тока и напряжения.
- Защита от замыкания на землю, реагирующая на токи и напряжения нулевой последовательности установившегося режима.
- Принцип действия продольной дифференциальной токовой защиты
- Схемы устройств автоматического повторного включения
- Схемы устройств автоматического включения резерва
- Защита и автоматика трансформаторов подстанций.
Похожие статьи вашей тематики
 В дальнейшем принимаем, что несимметрия возникает только в одном месте системы, а остальная часть системы остается строго симметричной. В дальнейшем принимаем, что несимметрия возникает только в одном месте системы, а остальная часть системы остается строго симметричной.
Анализ несимметричных переходных процессов затруднен из-за наличия пульсирующего магнитного поля ротора и связанных с ним гармоник. Суть процесса в следующем. Пусть по одной или двум фазам явно полной СМ без демпферных обмоток протекает ток синхронной частоты f, который создает неподвижный в пространстве пульсирующий магнитный поток, как это показано на рис.30. Этот поток Ф(f) разложим на два потока вращающихся с частотой ω в противоположные стороны. Поток, не совпадающий с направлением вращения ротора создает в обмотке возбуждения ЭДС удвоенной частоты (т.к. ротор вращается с частотой ω и один из потоков оказывается неподвижным по отношению к ротору). Обусловленный этой ЭДС ток удвоенной частоты создает пульсирующий поток удвоенной частоты. Разложение его на два потока, вращающихся с частотой 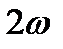 в противоположные стороны. При этом поток вращающийся в противоположную ротору сторону, оказывается неподвижным по отношению к ротору, а второй вращается с частотой в противоположные стороны. При этом поток вращающийся в противоположную ротору сторону, оказывается неподвижным по отношению к ротору, а второй вращается с частотой 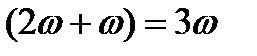 в сторону вращения ротора и наводит в обмотке статора ЭДС тройной синхронной частоты 3 f. В результате ток тройной частоты создает пульсирующий поток тройной частоты. Анализируя подробно процесс убеждаемся, что каждая нечетная гармоника однофазного переменного тока статора вызывает очередную четную гармонику в обмотке возбуждения, а каждая четная гармоника в обмотке возбуждения вызывает следующую нечетную гармонику тока статора. в сторону вращения ротора и наводит в обмотке статора ЭДС тройной синхронной частоты 3 f. В результате ток тройной частоты создает пульсирующий поток тройной частоты. Анализируя подробно процесс убеждаемся, что каждая нечетная гармоника однофазного переменного тока статора вызывает очередную четную гармонику в обмотке возбуждения, а каждая четная гармоника в обмотке возбуждения вызывает следующую нечетную гармонику тока статора.
При наличии демпферной обмотки в поперечной оси ротора, ротор (теоретически) оказывается симметричным в магнитном смысле, магнитное поле вращается, а, высшие гармонические не создаются. Однако практически ротор СМ не обладает такой симметрией, поэтому при любом несимметричном режиме СМ возникают высшие гармоники. Наличие демпферной обмотке только в продольной оси еще более усиливает несимметрию ротора, и только при наличии демпферных обмоток в обеих осях ротора достигается почти полная его симметрия.
Анализ несимметричных процессов значительно упрощается при использовании метода симметричных составляющих. Так как симметричные составляющие токов любой несимметричной системы связаны законом Ома с симметричными составляющими напряжений только одноименной последовательности, то симметричная составляющая падения напряжения на элементе, обладающем по отношению к симметричным составляющим токов прямой 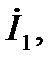 обратной обратной 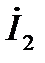 и нулевой и нулевой 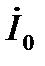 последовательностей соответственно сопротивлениями последовательностей соответственно сопротивлениями 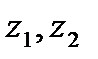 и и 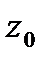 будут будут 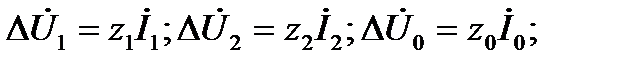
Комплексная форма записи справедлива не только для стационарного режима, но также и для переходного режима, поскольку токи и напряжения при переходном процессе можно представить проекциями на соответствующую ось вращающихся, а также неподвижных векторов. При этом уравнения могут быть представлены в операторном виде. Однако, из-за наличия высших гармоник в явнополюсных СМ при несимметричных режимах в подавляющем большинстве практических расчетов несимметричных переходных процессов обычно довольствуются учетом лишь основной гармоники токов и напряжений.
Именно только при таком ограничении представляется возможным применить метод симметричных составляющих в его обычной форме, характеризуя для этого СМ в схеме обратной последовательности соответствующей реактивностью 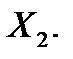
При анализе несимметричных режимов принимаем, что устройства АРВ СМ включены через фильтры прямой последовательности.
С учетом изложенного основные уравнения Кирхгофа для произвольного несимметричного короткого замыкания имеют вид:
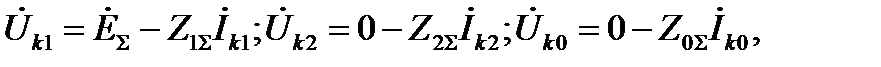 где где 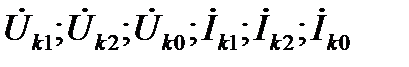 - симметричные составляющие напряжения и тока в месте короткого замыкания; - симметричные составляющие напряжения и тока в месте короткого замыкания; 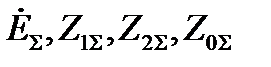 - соответственно результирующая ЭДС и сопротивления схем соответствующих последовательностей относительно точки короткого замыкания. - соответственно результирующая ЭДС и сопротивления схем соответствующих последовательностей относительно точки короткого замыкания.
Для определения искомых переменных эти три уравнения дополняют тремя уравнениями из граничных условий.
|