
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несимметричная нагрузка синхронного генератораСодержание книги
Поиск на нашем сайте
Несимметричная нагрузка возникает при не равномерном распределении однофазных приемников по фазам, а также при обрыве фаз и несимметричном установившимся коротком замыкании. При анализе несимметричного режима используется метод симметричных составляющих, согласно которому каждая из трех фаз может быть представлена в виде трех симметричных составляющих: прямой, обратной и нулевой последовательности.
Где
Системы различных последовательностей можно рассмотреть отдельно, предлагая, что насыщение отсутствует. Токи прямой последовательности создают МДС реакции якоря, вращающуюся синхронно с ротором, как это имеет место в СГ при симметричной нагрузке. При несимметрии нагрузки в СГ возникают токи обратной последовательности, которые создают обратно–синхронную МДС и обратное синхронное поле, которые вращаются с синхронной частотой в направлении противоположном вращению ротора. Токи нулевой последовательности создают лишь пульсирующие поля рассеяния, соответствующие высшим гармоникам Токи различных последовательностей можно определить через реальные несимметрические токи согласно следующим выражениям
Для других фаз имеем
где Выражения (3.5,…,3.7) справедливы и для несимметричной системы напряжений
С другой стороны это выражение можно записать в виде:
Сравнивая (3.8) и (3.9) будем иметь:
Здесь При симметрической нагрузке существуют лишь токи прямой последовательности и каждое из фазных напряжений СГ определяется первым уравнением системы (3.10). При этом где
В случае явнополюсной СМ будем иметь
Полное сопротивление обратной последовательности
Здесь При этом
Индуктивное сопротивление Сопротивление обратной последовательности можно определить экспериментально. Для этого надо замкнуть обмотку возбуждения и привести ротор во вращение с синхронной частотой вращения в сторону, противоположную вращению магнитного поля, которое создается статором. При выполнении опыта измеряется напряжение, ток и мощность.
В случае явнополюсной СМ обратное синхронное поле демпфируется по продольной и поперечной осям неодинаково. Поэтому, будут неодинаковые и полные сопротивления по продольной и поперечной осям В этом случае при определении сопротивления обратной последовательности следует исходить из среднего значения тока обратной последовательности
Так как Обычно Сопротивление нулевой последовательности
Несимметричная нагрузка сопровождается нежелательными явлениями. Обратное синхронное поле вызывает дополнительные потери в пассивных частях ротора и его обмотке (от токов двойной частоты.) При этом уменьшается КПД и сильно увеличивается температура ротора. Возможно искажение симметрии напряжений. В результате взаимодействия обратного синхронного поля и поля возбуждения появляется усилия двоичной частоты, что приводит к шуму и вибрации.
Несимметричные установившиеся короткие замыкания Несимметричные установившиеся короткие замыкания являются предельными случаями несимметричной нагрузки. Рассмотрим однофазное установившееся короткое замыкание (рис. 3.38,а).
Тогда напряжение фазы
отсюда
Установившийся ток однофазного короткого замыкания
При двухфазном установившемся коротком замыкании (рис.3.38,б) будем иметь
Токи прямой, обратной и нулевой последовательности соответственно будут
Напряжения фаз:
Отсюда имеем: или Преобразуя последнее уравнение с учетом изложенного выше, будем иметь
или Тогда Так как активные сопротивления невелики, то можно считать что
В соответствии с этим
Здесь
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.25.125 (0.008 с.) |

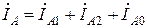 ,
, , (3.5)
, (3.5) .
. – токи прямой последовательности,
– токи прямой последовательности,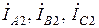 – токи обратной последовательности,
– токи обратной последовательности, – токи нулевой последовательности.
– токи нулевой последовательности. , а основная гармоника поля будет отсутствовать.
, а основная гармоника поля будет отсутствовать.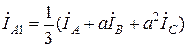 ,
, , (3.6)
, (3.6)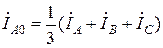 .
. ,
,  ,
,  ,
,  ,
,  , (3.7)
, (3.7) и
и  .
. . (3.8)
. (3.8) . (3.9)
. (3.9) ,
, , (3.10)
, (3.10) .
. – полные сопротивления прямой, обратной и нулевой последовательности.
– полные сопротивления прямой, обратной и нулевой последовательности. ,
,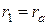 - активное сопротивление обмотки статора,
- активное сопротивление обмотки статора,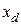 - синхронное индуктивное сопротивление неявнополюсной СМ.
- синхронное индуктивное сопротивление неявнополюсной СМ. – полное сопротивление прямой последовательности по продольной оси,
– полное сопротивление прямой последовательности по продольной оси, – полное сопротивление прямой последовательности по поперечной оси.
– полное сопротивление прямой последовательности по поперечной оси.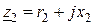 .
.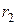 – активное сопротивление обратной последовательности.
– активное сопротивление обратной последовательности. , это связано с тем, что токи обратной последовательности обуславливают дополнительные потери в пассивных элементах ротора и успокоительной обмотке.
, это связано с тем, что токи обратной последовательности обуславливают дополнительные потери в пассивных элементах ротора и успокоительной обмотке.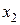 - индуктивное сопротивление обратной последовательности.
- индуктивное сопротивление обратной последовательности.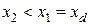 . Это связано с тем, что токи обратной последовательности создают обратное синхронное поле, вращающиеся с двойной синхронной скоростью относительно ротора. Следовательно, это поле наводит в элементах ротора и в частности в успокоительной обмотке, расположенной в полюсных наконечниках, токи двойной частоты, которые демпфируют обратное поле, существенно уменьшая его.
. Это связано с тем, что токи обратной последовательности создают обратное синхронное поле, вращающиеся с двойной синхронной скоростью относительно ротора. Следовательно, это поле наводит в элементах ротора и в частности в успокоительной обмотке, расположенной в полюсных наконечниках, токи двойной частоты, которые демпфируют обратное поле, существенно уменьшая его. .
. .
. ,
, .
. , то
, то  .
.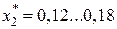 для неявнополюсных СГ,
для неявнополюсных СГ,  для явнополюсных СГ.
для явнополюсных СГ.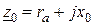 , где
, где  ,
,  – индуктивное сопротивление нулевой последовательности, (
– индуктивное сопротивление нулевой последовательности, (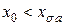 при укороченном шаге). Сопротивление нулевой последовательности можно определить экспериментально. При этом обмотку возбуждения замыкают накоротко, и ротор приводят во вращение с синхронной скоростью. Фазные обмотки статора соединяются последовательно, и к ним подводится напряжение (рис. 3.37).
при укороченном шаге). Сопротивление нулевой последовательности можно определить экспериментально. При этом обмотку возбуждения замыкают накоротко, и ротор приводят во вращение с синхронной скоростью. Фазные обмотки статора соединяются последовательно, и к ним подводится напряжение (рис. 3.37).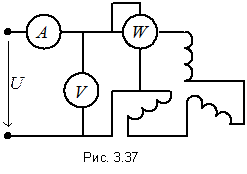
 .
. В этом случае
В этом случае  ,
, 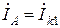 ,
,  . Токи прямой, обратной и нулевой последовательности соответственно будут
. Токи прямой, обратной и нулевой последовательности соответственно будут .
. ,
, .
. .
.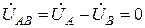 ,
,  ,
, ,
,  .
. ,
,  ,
, .
.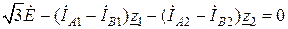
 .
.
 .
. .
. .
. ,
,  ,
,  .
. Последние выражения позволяют определить индуктивные сопротивления прямой, обратной и нулевой последовательности (рис. 3.39), если известна характеристика холостого хода, а также характеристик одно–, двух и трехфазного симметричного короткого замыкания.
Последние выражения позволяют определить индуктивные сопротивления прямой, обратной и нулевой последовательности (рис. 3.39), если известна характеристика холостого хода, а также характеристик одно–, двух и трехфазного симметричного короткого замыкания. ;
; 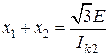 ;
;  ;
;  ;
; 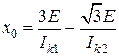 .
. – индуктивное сопротивление прямой последовательности,
– индуктивное сопротивление прямой последовательности, – индуктивное сопротивление нулевой последовательности.
– индуктивное сопротивление нулевой последовательности.


