
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоскости, проходящей через три данные точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости Возьмем на плоскости произвольную точку
Раскрывая определитель по элементам первой строки, получим уравнение плоскости вида (1), т. е. уравнение (2) есть уравнение плоскости, проходящей через три данные точки. Уравнение плоскости в отрезках на осях Пусть плоскость отсекает на осях
Раскрыв определитель, имеем
Уравнение (3) называется уравнением плоскости в отрезках на осях. Им удобно пользоваться при построении плоскости. Основные задачи, использующие уравнения плоскости. Угол между двумя плоскостями. Условия параллельности И перпендикулярности двух плоскостей. Пусть заданы две плоскости
Под углом между плоскостями Угол Поэтому угол можно найти как угол между нормалями плоскостей по известной формуле
или
Для нахождения острого угла следует взять модуль правой части. Если плоскости
Полученное равенство есть условие перпендикулярности двух плоскостей Если плоскости
Это и есть условие параллельности двух плоскостей Расстояние от точки до плоскости. Пусть задана точка
Вывод этой формулы такой же, как вывод формулы расстояния от точки Уравнения прямой в пространстве. Векторное уравнение прямой. Положение прямой в пространстве вполне определено, если задать какую-либо точку
Вектор
В результате получим уравнение
Полученное уравнение называется векторным уравнением прямой.
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 618; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.009 с.) |

 , проходящей через три данные точки
, проходящей через три данные точки  ;
;  и
и  , не лежащие на одной прямой.
, не лежащие на одной прямой. и составим векторы
и составим векторы  ,
,  ,
,  . Эти векторы лежат на плоскости
. Эти векторы лежат на плоскости  . Смешанное произведение векторов можно вычислить через определитель третьего порядка:
. Смешанное произведение векторов можно вычислить через определитель третьего порядка: . (2)
. (2) ,
,  и
и  соответственно отрезки
соответственно отрезки  ,
,  и
и  , т. е. проходит через три точки
, т. е. проходит через три точки  ,
,  и
и  (рис.1).
(рис.1). Подставляя координаты этих точек в уравнение (2), получаем
Подставляя координаты этих точек в уравнение (2), получаем
 .
. , т. е.
, т. е.  или
или . (3)
. (3) и
и  общими уравнениями:
общими уравнениями: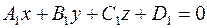 ,
, .
. между нормальными векторами
между нормальными векторами  и
и  плоскостей
плоскостей 
 . (4)
. (4) (и наоборот). Но тогда скалярное произведение нормалей равно нулю:
(и наоборот). Но тогда скалярное произведение нормалей равно нулю:  , т. е.
, т. е. . (5)
. (5) и
и  (и наоборот). Но тогда, как известно, координаты векторов пропорциональны:
(и наоборот). Но тогда, как известно, координаты векторов пропорциональны: . (6)
. (6) и плоскость
и плоскость  . Расстояние
. Расстояние  от точки
от точки  до плоскости
до плоскости  . (7)
. (7) до прямой
до прямой 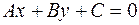 .
. на прямой и вектор
на прямой и вектор  , параллельный этой прямой. Вектор
, параллельный этой прямой. Вектор  задана ее точкой
задана ее точкой  . Возьмем на прямой
. Возьмем на прямой  соответственно через
соответственно через  и
и  . Очевидно, что три вектора
. Очевидно, что три вектора  связаны соотношением
связаны соотношением . (8)
. (8) , где
, где  — скалярный множитель, называемый параметром, может принимать различные значения в зависимости от положения точки
— скалярный множитель, называемый параметром, может принимать различные значения в зависимости от положения точки 

 (9)
(9)


