
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: аналитическая геометрия в пространствеСодержание книги
Поиск на нашем сайте
Тема: АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ Л е к ц и я 6 ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ ПЛАН Поверхность и ее уравнение. Уравнения плоскости в пространстве. Основные задачи, использующие уравнения плоскости. Уравнения прямой в пространстве. Основные задачи, использующие уравнения прямой в пространстве. Взаимное расположение прямой и плоскости в пространстве. Поверхность и ее уравнение. Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса Уравнением данной поверхности в прямоугольной системе координат Уравнения плоскости в пространстве. Простейшей поверхностью является плоскость. Плоскость в пространстве Общее уравнение плоскости Общим уравнением плоскости называется уравнение первой степени с тремя переменными
причем по крайней мере один из коэффициентов Вектор Частные случаи общего уравнения плоскости: 1. Если
Этому уравнению удовлетворяет точка 2. Если 3. Если 4. Если 5. Если Основные задачи, использующие уравнения плоскости. Угол между двумя плоскостями. Условия параллельности Уравнения прямой в пространстве. Векторное уравнение прямой. Положение прямой в пространстве вполне определено, если задать какую-либо точку
Вектор
В результате получим уравнение
Полученное уравнение называется векторным уравнением прямой. Тема: АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ Л е к ц и я 6
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 359; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.52.104 (0.006 с.) |

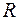 с центром в точке
с центром в точке 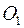 есть геометрическое место всех точек пространства, находящихся от точки
есть геометрическое место всех точек пространства, находящихся от точки 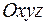 называется такое уравнение
называется такое уравнение 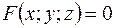 с тремя переменными х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х, у и z в уравнении поверхности называются текущими координатами точек поверхности.
с тремя переменными х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х, у и z в уравнении поверхности называются текущими координатами точек поверхности.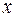 ,
, 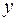 и
и 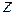 :
: , (1)
, (1)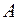 ,
, 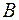 или
или 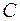 не равен нулю.
не равен нулю.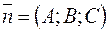 называется нормальным вектором плоскости, он перпендикулярен плоскости (1).
называется нормальным вектором плоскости, он перпендикулярен плоскости (1).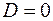 , то уравнение (1) принимает вид
, то уравнение (1) принимает вид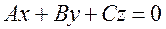 .
.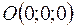 . Следовательно, в этом случае плоскость проходит через начало координат.
. Следовательно, в этом случае плоскость проходит через начало координат.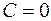 , то имеем уравнение
, то имеем уравнение 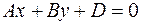 . Нормальный вектор
. Нормальный вектор 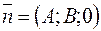 перпендикулярен оси
перпендикулярен оси  . Следовательно, плоскость параллельна оси
. Следовательно, плоскость параллельна оси  ,
, 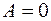 – параллельна оси
– параллельна оси  .
.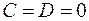 , то уравнение плоскости примет вид
, то уравнение плоскости примет вид 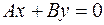 , в этом случае плоскость проходит через ось
, в этом случае плоскость проходит через ось 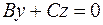 и
и 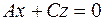 отвечают плоскости, проходящие соответственно через оси
отвечают плоскости, проходящие соответственно через оси 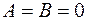 , то уравнение (1) принимает вид
, то уравнение (1) принимает вид 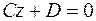 , т. е.
, т. е. 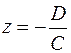 . Плоскость параллельна плоскости
. Плоскость параллельна плоскости 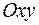 . Аналогично, уравнениям
. Аналогично, уравнениям 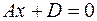 и
и 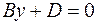 отвечают плоскости, соответственно параллельные плоскостям
отвечают плоскости, соответственно параллельные плоскостям 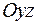 и
и 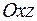 .
.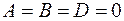 , то уравнение (1) примет вид
, то уравнение (1) примет вид 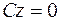 , т. е.
, т. е. 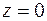 . Это уравнение плоскости
. Это уравнение плоскости 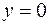 — уравнение плоскости
— уравнение плоскости 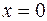 — уравнение плоскости
— уравнение плоскости  на прямой и вектор
на прямой и вектор  , параллельный этой прямой. Вектор
, параллельный этой прямой. Вектор  задана ее точкой
задана ее точкой  и направляющим вектором
и направляющим вектором  . Возьмем на прямой
. Возьмем на прямой  . Обозначим радиус-векторы точек
. Обозначим радиус-векторы точек  соответственно через
соответственно через  и
и  . Очевидно, что три вектора
. Очевидно, что три вектора  связаны соотношением
связаны соотношением . (8)
. (8) , где
, где  — скалярный множитель, называемый параметром, может принимать различные значения в зависимости от положения точки
— скалярный множитель, называемый параметром, может принимать различные значения в зависимости от положения точки 

 (9)
(9)


