Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность сложной функцииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема. Пусть функция z = Доказательство 1. Для доказательства теоремы воспользуемся определением непрерывности функции в точке на “языке последовательностей”. 2. Возьмём из множества X любую последовательность точек: 3. Тогда соответствующая последовательность значений функции будет иметь вид: 4. По условию теоремы функция z =
5. Тогда и предел соответствующей последовательности значений функции 6. Последнее утверждение означает, что некоторая последовательность { z n} сходится к z 0 при n ® ¥: 7. По условию теоремы функция y = f (z) непрерывна в точке z 0 = j(x 0), при 8. Тогда по определению непрерывности функции в точке на «языке последовательностей»: соответствующая последовательность значений функции { f (z n)} будет сходится к f (z 0) при n ® ¥: 9. С учётом того, что z n = j(x n), z 0 = j (x 0) перепишем последнее равенство:
10. Так как произвольная последовательность значений аргумента "{ x n} сходится к x 0 при n ® ¥:
ч.т.д. Замечание. 1. Так как
т.е. операция предельного перехода перестановочна с операцией взятия непрерывной функции. 2. При отыскании пределов непрерывных функций эту тему удобно использовать в виде правила замены непрерывной переменной. 3. Так пусть z = j (x) непрерывна в точке х 0, а функция y = f (z) непрерывна в точке z 0 = j (x 0). Тогда Пример. Найти предел Решение 1. Пусть 2. Воспользуемся правилом замены переменной, получим:
Точки разрыва монотонных функций Определение 1 Функция Определение 2 Если при условии Определение 3 Все виды указанных в определениях №№ 1 и 2 функций объединяют под общим названием монотонных. Но возрастающие и убывающие функции называют строго монотонными. Теорема 1 Монотонно невозрастающая (неубывающая) функция Доказательство Доказательство данной теоремы очевидно. Оно следует из определения функции в точке и на промежутке, а также из определения монотонности функции. Очевидно, что если функция Теорема 2 Монотонная функция может иметь точки разрыва только первого рода. Доказательство 1. Пусть функция 2. Будем считать для определённости 3. Возьмем любую внутреннюю точку отрезка 4. Так как точка 5. Поэтому множество значений функции 6. Очевидно, что 7. Согласно определению верхней грани для 8. Так как функция
9. В соответствии с определением левого предела функции в точке:
10. Или 11. Очевидно, что 12. Аналогично доказывается, что в точке 13. Если левый и правый пределы существуют, а это уже доказано, и совпадают со значением функции в точке 14. Если же, по крайней мере, один из этих пределов не равен Замечание Для убывающей функции доказательства теоремы проводится аналогично. Инъективные функции Определение Функция Если Так всякая строго монотонная функция, определённая во множестве действительных чисел, инъективна. Но обратное утверждение неверно. Пример Так функция Теорема Непрерывная и инъективная функция
ﻫ Непрерывность обратной функции Понятие обратной функции Определение Пусть Если в каждой упорядоченной паре этого множества числа Обозначают обратную функцию так: Замечание Обратная функция, вообще говоря, не является функцией, так как каждое число Пример 1. Для функции 2. Для функции
3. Для функции
Геометрически данный факт очевиден.
Замечание Из определения следует, что если обратная функция однозначна, т.е. является функцией в обычном смысле, то множество значений функции График обратной функции Перейдём к выяснению вопроса о взаимном расположении графиков прямой и обратной функций. 1. Так как связь между переменными
2. Если же обратную функцию представить в обычно принятых обозначениях: аргумент обозначить за 3. Если аргумент функции
4. Чтобы получить его новое расположение нужно перегнуть плоскость чертежа по биссектрисе первого и третьего координатных углов. Можно сказать, что график обратной функции является зеркальным отражением (отображением) графика прямой функции Пример
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 963; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.139 (0.011 с.) |

 непрерывна в точке х 0, а функция y = f (z) непрерывна в точке z 0 = j(x 0). Тогда сложная функция
непрерывна в точке х 0, а функция y = f (z) непрерывна в точке z 0 = j(x 0). Тогда сложная функция  непрерывна в точке х 0, т.е.
непрерывна в точке х 0, т.е.  .
. сходящихся к x 0: { x n} ® x 0 при n ® ¥ или
сходящихся к x 0: { x n} ® x 0 при n ® ¥ или 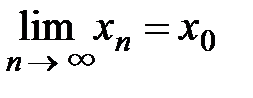 . X – область определения функции
. X – область определения функции  .
. .
. непрерывна в точке х 0, т.е.
непрерывна в точке х 0, т.е.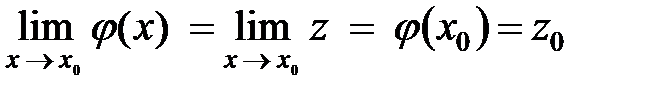 .
. {j(xn)} тоже будет равен z 0 или j(x 0):
{j(xn)} тоже будет равен z 0 или j(x 0):  (на основании определения непрерывных функций в точке на «языке последовательностей»).
(на основании определения непрерывных функций в точке на «языке последовательностей»). :
:  .
. :
: 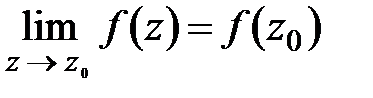 .
. .
. .
. , а соответствующая ей последовательность значений функции { f [j(x n)]} сходится к f [j(x 0)] при n ®¥:
, а соответствующая ей последовательность значений функции { f [j(x n)]} сходится к f [j(x 0)] при n ®¥: 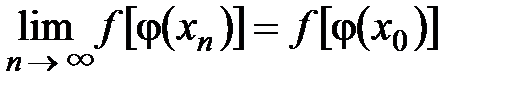 , то, согласно определения непрерывности функции в точке на “языке последовательностей”, сама функция y = f [
, то, согласно определения непрерывности функции в точке на “языке последовательностей”, сама функция y = f [  . А это есть условие непрерывности сложной функции
. А это есть условие непрерывности сложной функции  в точке x = х 0.
в точке x = х 0. , то утверждение теоремы можно записать в виде формулы:
, то утверждение теоремы можно записать в виде формулы: вместо
вместо 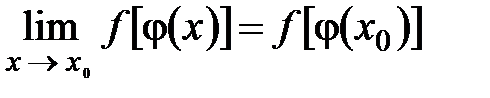 ,
,

 . Тогда при
. Тогда при  .
.
 , заданная на некотором промежутке, называется возрастающей (убывающей) на этом промежутке, если для любой пары точек промежутка:
, заданная на некотором промежутке, называется возрастающей (убывающей) на этом промежутке, если для любой пары точек промежутка:  и
и 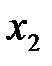 , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется соотношение
, выполняется соотношение  (
( ).
). выполняется соотношение
выполняется соотношение 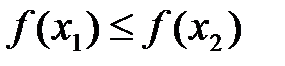 (или соотношение
(или соотношение  ), то
), то  называется неубывающей (невозрастающей) на этом промежутке.
называется неубывающей (невозрастающей) на этом промежутке. , заданная на некотором промежутке, имеет конечные односторонние пределы в каждой точке этого промежутка.
, заданная на некотором промежутке, имеет конечные односторонние пределы в каждой точке этого промежутка. , то она на этом отрезке ограничена, имеет наибольшее и наименьшее значения, которые принимаются функцией на концах отрезка.
, то она на этом отрезке ограничена, имеет наибольшее и наименьшее значения, которые принимаются функцией на концах отрезка.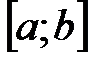 .
.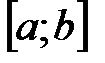 .
. , т.е.
, т.е.  .
. не самая левая точка отрезка
не самая левая точка отрезка 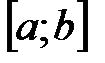 , то на полуотрезке
, то на полуотрезке 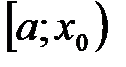 функция
функция  ограничена сверху, ибо выполняется неравенство
ограничена сверху, ибо выполняется неравенство  при
при  ,
,  .
. имеет точную верхнюю грань
имеет точную верхнюю грань  в соответствии с теоремой «всякое непустое ограниченное сверху множество имеет точную верхнюю грань».
в соответствии с теоремой «всякое непустое ограниченное сверху множество имеет точную верхнюю грань». , так как функция
, так как функция  , а
, а  .
. найдётся такая точка
найдётся такая точка  , что при
, что при 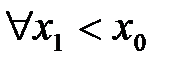 будет выполняться неравенство
будет выполняться неравенство  .
. , удовлетворяющих неравенству
, удовлетворяющих неравенству  тем более будет верно неравенство
тем более будет верно неравенство .
.
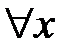 :
:  ,
, 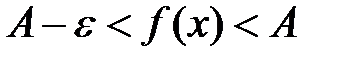 .
. 
 .
.  – левый предел.
– левый предел. .
. .
. функция
функция  имеет и правый предел
имеет и правый предел  , причём
, причём  .
. , то функция
, то функция  , то точка
, то точка  , то
, то  .
. инъективна, но не монотонна на множестве действительных чисел.
инъективна, но не монотонна на множестве действительных чисел. , строго монотонна.
, строго монотонна. и
и 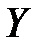 - некоторые множества. И пусть задана функция
- некоторые множества. И пусть задана функция  , причем
, причем  ,
,  . Во множестве упорядоченных пар чисел
. Во множестве упорядоченных пар чисел  каждое
каждое  входит в одну и только одну пару, а каждое число
входит в одну и только одну пару, а каждое число 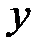 , по крайней мере, в одну пару.
, по крайней мере, в одну пару. поменять местами, то получим множество упорядоченных пар чисел
поменять местами, то получим множество упорядоченных пар чисел  , которое называется обратной функцией к функции
, которое называется обратной функцией к функции  .
. ,
,  или
или  .
. обратная функция
обратная функция  однозначна, поскольку каждое
однозначна, поскольку каждое  входит только в одну пару чисел
входит только в одну пару чисел  обратная функция
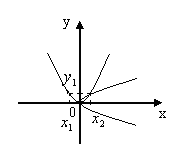
обратная функция  двузначна (так как каждое
двузначна (так как каждое  ,
,  ).
).
 обратная функция
обратная функция  – многозначная (каждое
– многозначная (каждое  ,
,  ,
,  …).
…).
 ) является областью определения обратной функции
) является областью определения обратной функции  . А область определения функции
. А область определения функции  ) является множеством значений обратной функции
) является множеством значений обратной функции  .
. и
и 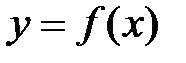 и обратной ей функции
и обратной ей функции  одна и та же, то графики этих функций совпадают.
одна и та же, то графики этих функций совпадают.
 . При этом функцию
. При этом функцию  мы по-прежнему будем называть обратной по отношению к функции
мы по-прежнему будем называть обратной по отношению к функции  .
.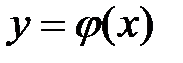 откладывать по горизонтальной оси, то график обратной функции повернётся.
откладывать по горизонтальной оси, то график обратной функции повернётся.
 в биссектрисе первого и третьего координатных углов.
в биссектрисе первого и третьего координатных углов. - прямая функция.
- прямая функция.  - ей обратная. В стандартном виде обратная функция будет иметь вид
- ей обратная. В стандартном виде обратная функция будет иметь вид  .
.