
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Степенная функция с натуральным показателем
Степенной функцией с натуральным показателем n называют функцию
Определение этой функции общеизвестно y=x для n>1 Из самого ее определения следует, что при любом натуральном k:
Функция
 , то , то  , а потому график функции , а потому график функции 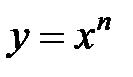 проходит через начало координат(рис.1) [4]. проходит через начало координат(рис.1) [4].
Исследуем функцию Вначале проведем это исследование на полусегменте Пусть
Так как Поскольку функция Функция По теореме о бесконечно больших функциях получаем, что б) Пусть
Если Эта функция строго возрастает при Функция По теоремам о бесконечно больших функциях получаем, что
П. 2. Степенная функция с целым отрицательным показателем
Определение: Степенной функцией с целым отрицательным показателем называют функцию Функцию Для а) Пусть
Функция Как и в случае натурального показателя б) Пусть m - чётное, m = 2k, k
Тогда функция непрерывна на всей области определения, исключая точку 0. Функция
При положительных При этом Модуль Тема №5 Непрерывность основных Элементарных функций. Равномерная непрерывность функции на множестве Лекция №19 1. Функция арифметического корня 2. Свойства арифметического корня. 3. Функция корня при n - нечетном. 4. Степенная функция во множестве действительных чисел. 5. Степенно – показательная функция. 6. Некоторые пределы, связанные с показательными и логарифмическими функциями. 7. Обратные тригонометрические функции.
|
||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 521; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.51.241 (0.006 с.) |
 , где n Î N, x Î R. (1)
, где n Î N, x Î R. (1) и
и 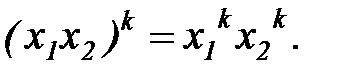
 определена на всей числовой оси[9].
определена на всей числовой оси[9].
 - нечетно, т. е.
- нечетно, т. е.  , k
, k  N, тогда функция
N, тогда функция  - нечетная.
- нечетная. [9].
[9]. имеем:
имеем:
 , то
, то  , а так как
, а так как  и
и  , то и
, то и  , следовательно,
, следовательно,  , т. е. функция (1) монотонно возрастает на полусегменте
, т. е. функция (1) монотонно возрастает на полусегменте 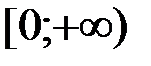 [4].
[4]. нечетная, то на полусегменте
нечетная, то на полусегменте  монотонно возрастает, так как если
монотонно возрастает, так как если  , то
, то  .
. непрерывна на всей числовой оси, как
непрерывна на всей числовой оси, как  непрерывных функций
непрерывных функций  .
. и
и  [2].
[2]. ,
,  .
. Тогда функция - четная функция. Очевидно так же, что при четном
Тогда функция - четная функция. Очевидно так же, что при четном  , то
, то  , следовательно, график функции проходит через начало координат (рис.2).
, следовательно, график функции проходит через начало координат (рис.2). , так как при
, так как при 
 . А на полуоси
. А на полуоси 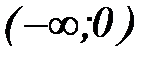 функция строго убывает, так как если
функция строго убывает, так как если  , то
, то  .
. непрерывна на всей числовой прямой, как произведение
непрерывна на всей числовой прямой, как произведение 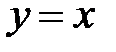 , непрерывность которых уже доказана [4].
, непрерывность которых уже доказана [4]. ,
,  .
. , где
, где  . (2)
. (2) выражение
выражение  не определяют, так что областью определения функции (2) является совокупность двух интервалов
не определяют, так что областью определения функции (2) является совокупность двух интервалов  [9].
[9]. - нечетное, m=2k- 1, k
- нечетное, m=2k- 1, k  N.
N.
 непрерывна на всей числовой прямой, исключая точку x=0.
непрерывна на всей числовой прямой, исключая точку x=0. нечетна. Так как при положительных x
нечетна. Так как при положительных x  и
и  из неравенства
из неравенства  следует неравенство
следует неравенство  , то на интервале
, то на интервале  функция (2) монотонно убывает. Отсюда в свою очередь следует, что в интервале
функция (2) монотонно убывает. Отсюда в свою очередь следует, что в интервале  функция строго убывает, т.е. функция строго убывает на области определения, при этом
функция строго убывает, т.е. функция строго убывает на области определения, при этом 
 ,
,  и
и  [4].
[4]. N.
N.
 четна, т. е. она неотрицательна для всех
четна, т. е. она неотрицательна для всех  из своей области определения.
из своей области определения. и
и  следует что на интервале
следует что на интервале  функция монотонно убывает. А в интервале
функция монотонно убывает. А в интервале  функция монотонно возрастает, так как из
функция монотонно возрастает, так как из  следует неравенство
следует неравенство  .
.
 и
и  ,
,  [2].
[2]. .
.


