
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства гиперболических функцийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
1. Так как функции 2. Так как
то функция 3. Так как
то функция 4. Так как
то функция 5. Так как
то функция 6. На промежутке а) 7. На промежутке а) 8. На промежутке
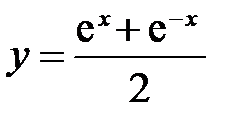 возрастает от 1 до возрастает от 1 до  на промежутке на промежутке  . Но . Но 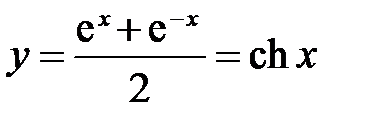 , значит, функция , значит, функция 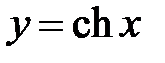 возрастает от 1 до возрастает от 1 до 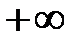 на промежутке на промежутке  (рис.7). (рис.7).
10. На промежутке
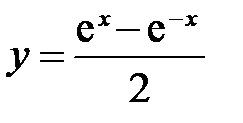 возрастает от 0 до возрастает от 0 до 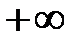 на промежутке на промежутке  . Но . Но 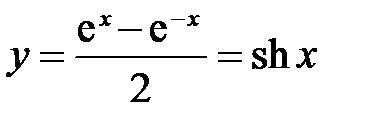 , значит, функция , значит, функция  возрастает от 0 до возрастает от 0 до 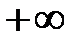 на промежутке на промежутке  (рис.8). (рис.8).
12. На промежутке
13. Но
14. На промежутке
 , значит, функция , значит, функция 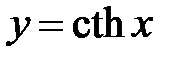 убывает от убывает от 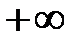 до 1 на промежутке до 1 на промежутке  (рис.10). (рис.10).
16. Заметим, что из всех гиперболических функций только одна функция гиперболического тангенса является ограниченной: 17. Кривая 9. Непрерывные и равномерно непрерывные функции на Определение №2. Функция Определение №3. Функция
Примеры: 1. Функция 2. Функция Доказательство: 1. Возьмем из 2. Тогда
3. Очевидно, что при каждом определенном значении
4. Поэтому в любой точке
если только 5. Это доказывает непрерывность 6. Возьмем теперь из 7. Тогда
8. Очевидно, что если значение при 9. Поэтому для будет
10. Это доказывает, что функция Равномерная непрерывность функции на промежутке означает, что в любом месте этого промежутка одна и та же разность значений аргументов Понятие равномерной непрерывности функции относится к наиболее сложным и трудным для усвоения понятиям математического анализа.
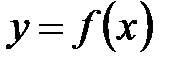 есть некоторая тонкая, но жесткая стальная нить. Задача состоим в том, чтобы изготовить такую муфту длины есть некоторая тонкая, но жесткая стальная нить. Задача состоим в том, чтобы изготовить такую муфту длины 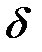 с цилиндрическим отверстием диаметра с цилиндрическим отверстием диаметра 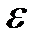 (Рис.11), которая могла бы свободно передвигаться вдоль этой стальной нити от точки (Рис.11), которая могла бы свободно передвигаться вдоль этой стальной нити от точки 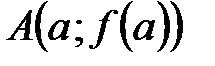 до точки до точки 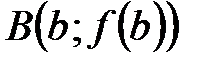 , сохраняя при этом положение, , сохраняя при этом положение,  при котором ее ось параллельна оси при котором ее ось параллельна оси 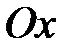 . Очевидно, что длина . Очевидно, что длина 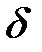 такой фунты будет зависеть только от величины диаметра ее отверстия такой фунты будет зависеть только от величины диаметра ее отверстия 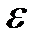 : чем меньше диаметр отверстия : чем меньше диаметр отверстия 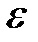 , тем короче должна быть муфта, тем меньше должно быть , тем короче должна быть муфта, тем меньше должно быть 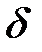 . Если для заданной кривой . Если для заданной кривой 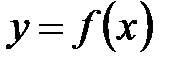 такую муфту можно изготовить с любым сколь угодно малым наперед заданным диаметром такую муфту можно изготовить с любым сколь угодно малым наперед заданным диаметром 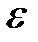 , то функция , то функция  равномерно непрерывна на равномерно непрерывна на  . Действительно, в этом случае для любой пары точек . Действительно, в этом случае для любой пары точек  и и  , удовлетворяющих неравенству , удовлетворяющих неравенству  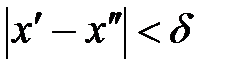 , будет выполняться неравенство , будет выполняться неравенство 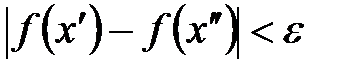 . .Пытаясь построить такую модель для функции Пытаясь построить такую модель для функции
Тем более интересна следующая теорема, которая показывает, что если функция Теорема Кантора Теорема. Если функция Доказательство: 1. Доказательство проведем методом от противного. 2. Допустим, что функция 3. Это означает, что не для любого 4. Поэтому существует такое
5. Возьмем последовательность значений
6. Для Для …………………………………………………………………………………. Для ………………………………………………………………………………… Этот процесс продолжаем бесконечно. 7. В результате из отрезка
8. Рассмотрим последовательность 9. Пусть это будет подпоследовательность
Причем, очевидно, что 10. По условию теоремы функция
11. В соответствии с определением непрерывности функции в точке на языке последовательностей: соответствующая последовательность значений функции
12. Из неравенства
Действительно:
или
Так как если 13. Тогда соответствующая последовательность значений функции
14. Равенства п. 11 и п. 13 можно переписать в виде таких неравенств при следующих условиях
15.
и
16. По свойству модуля разности двух действительных чисел:
или
17. Но по самому выбору точек
18. Следовательно, функция ч.т.д. Замечание. То, что в условии берется отрезок, является существенным. Так, например, функция Колебание функции 1. Из первой теоремы Вейерштрасса следует, что если функция 2. Обозначим через Определение №4. Колебанием функции
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.181.69 (0.01 с.) |

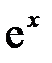 и
и 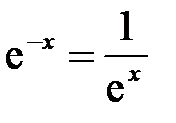 определены и непрерывны на промежутке
определены и непрерывны на промежутке 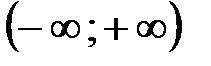 , то по теореме о непрерывности суммы, разности и частного непрерывных функций следует, что гиперболические функции
, то по теореме о непрерывности суммы, разности и частного непрерывных функций следует, что гиперболические функции 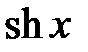 ,
, 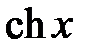 ,
, 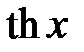 ,
, 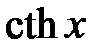 также определены и непрерывны на промежутке
также определены и непрерывны на промежутке  (за исключением точки
(за исключением точки  для
для  ,
, – четная, а значит, график функции симметричен относительно оси
– четная, а значит, график функции симметричен относительно оси 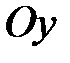 .
. ,
, – нечетная, а значит, график функции симметричен относительно начала координат.
– нечетная, а значит, график функции симметричен относительно начала координат. ,
, – нечетная, а значит, график функции симметричен относительно начала координат.
– нечетная, а значит, график функции симметричен относительно начала координат.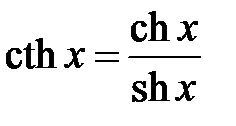 ,
, – нечетная, а значит, график функции симметричен относительно начала координат.
– нечетная, а значит, график функции симметричен относительно начала координат.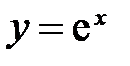 возрастает от 1 до
возрастает от 1 до 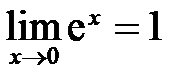 ; б)
; б) 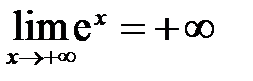 .
.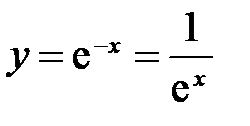 убывает от 1 до 0, так как
убывает от 1 до 0, так как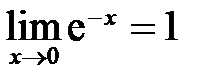 ; б)
; б) 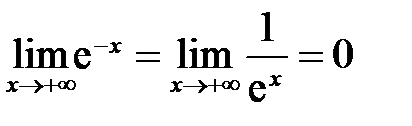 .
.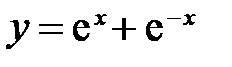 возрастает от 2 до
возрастает от 2 до 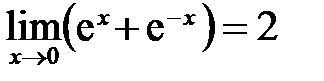 ; б)
; б) 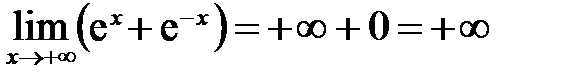 .
.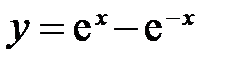 возрастает от 0 до
возрастает от 0 до  а)
а) 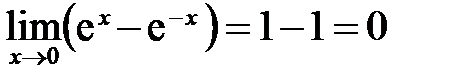 ; б)
; б)  .
.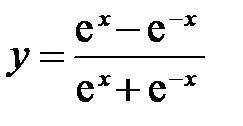 возрастает от 0 до 1, так как
возрастает от 0 до 1, так как 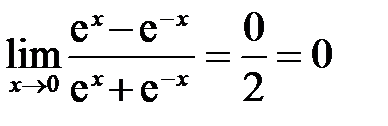 ; б)
; б) 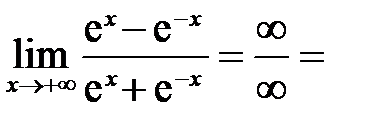

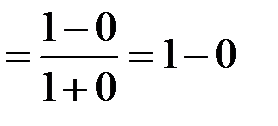 .
. , значит, функция
, значит, функция 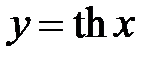 возрастает от 0 до 1 на промежутке
возрастает от 0 до 1 на промежутке 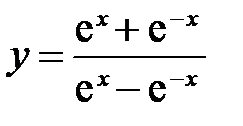 убывает от
убывает от 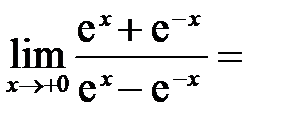
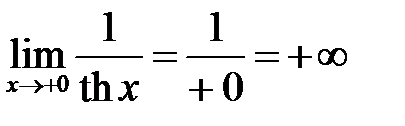 ; б)
; б) 
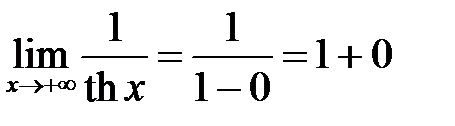 .
.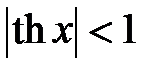 .
. носит название цепной линии. Это название кривая получила из-за того, что цепь или канат, закреплённые с двух концов, принимают под действием собственного веса такую форму прогиба.
носит название цепной линии. Это название кривая получила из-за того, что цепь или канат, закреплённые с двух концов, принимают под действием собственного веса такую форму прогиба.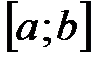
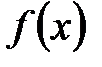 называется непрерывной на отрезке
называется непрерывной на отрезке 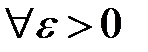 можно найти такое
можно найти такое 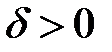 , что для любых
, что для любых 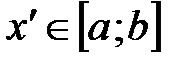 и
и 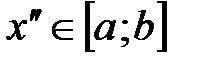 , удовлетворяющих условию
, удовлетворяющих условию 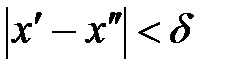 , выполняется неравенство:
, выполняется неравенство: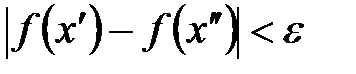 .
. равномерно непрерывна на всей числовой прямой. Достаточно взять
равномерно непрерывна на всей числовой прямой. Достаточно взять  , так как
, так как 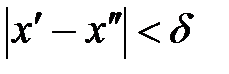 и
и 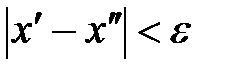
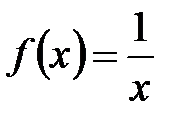 на
на 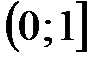 непрерывна, но не является равномерно непрерывной. Докажем это.
непрерывна, но не является равномерно непрерывной. Докажем это.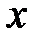 и
и 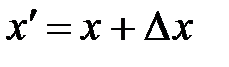 .
.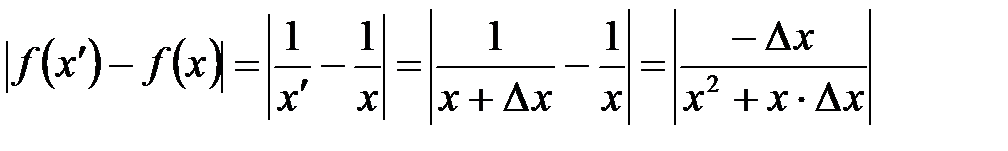 .
. из полуинтервала
из полуинтервала  .
.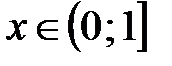 по заданному
по заданному 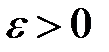 можно найти такое
можно найти такое 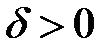 , что будет верно неравенство:
, что будет верно неравенство: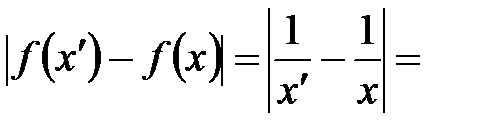

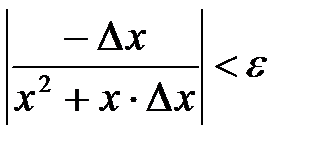 ,
, .
.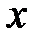 из
из 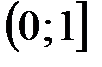 .
.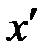 и
и  .
.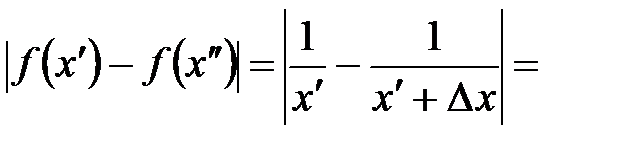
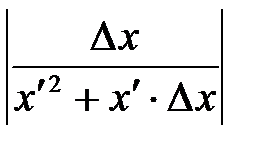 .
.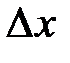 , как угодно мало, но уже выбрано, то
, как угодно мало, но уже выбрано, то величина
величина 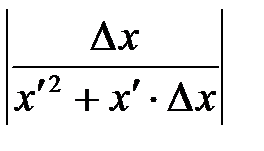 неограниченно возрастает.
неограниченно возрастает.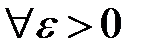 , каким бы малым
, каким бы малым 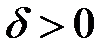 ни было, всегда можно найти на полуинтервале
ни было, всегда можно найти на полуинтервале  и
и  , что
, что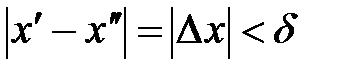 и тем не менее окажется, что
и тем не менее окажется, что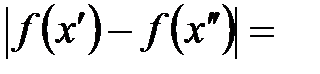

 .
.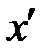 и
и  обеспечивает заданную выбором
обеспечивает заданную выбором 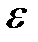 разницу соответствующих значений функций
разницу соответствующих значений функций 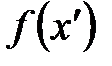 и
и 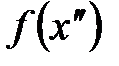 .
.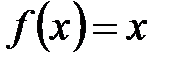 , легко убедиться, что она является равномерно непрерывной на
, легко убедиться, что она является равномерно непрерывной на  .
.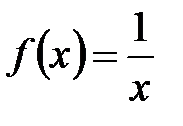 , легко убедиться, что она на
, легко убедиться, что она на  мы ее не изготовили (Рис.12) [2].
мы ее не изготовили (Рис.12) [2]. непрерывна на отрезке, то она обладает свойством равномерной непрерывности.
непрерывна на отрезке, то она обладает свойством равномерной непрерывности. непрерывна на отрезке
непрерывна на отрезке  , то она равномерно непрерывна на этом отрезке.
, то она равномерно непрерывна на этом отрезке.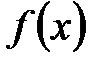 , непрерывная на отрезке
, непрерывная на отрезке 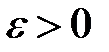 можно найти такое
можно найти такое  , чтобы из неравенства
, чтобы из неравенства  всегда выполнялось неравенство
всегда выполнялось неравенство 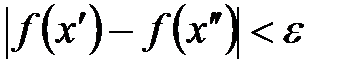 .
.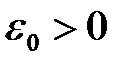 , что каким бы малым
, что каким бы малым 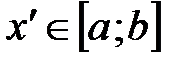 и
и 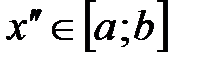 , что хотя и будет выполняться неравенство
, что хотя и будет выполняться неравенство 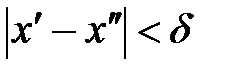 , тем не менее окажется, что
, тем не менее окажется, что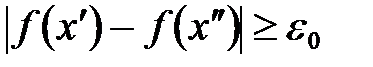 .
. , сходящуюся к нулю:
, сходящуюся к нулю: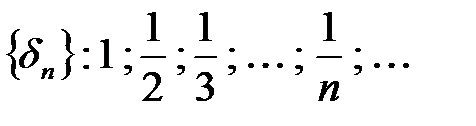 ,
,  ,
,  .
.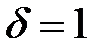 найдутся на отрезке
найдутся на отрезке  и
и 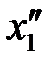 , что вслед за неравенством
, что вслед за неравенством 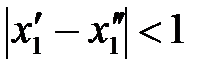 будет выполняться
будет выполняться 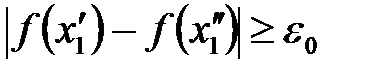 .
.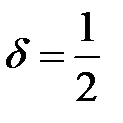 найдутся на отрезке
найдутся на отрезке  и
и  , что вслед за неравенством
, что вслед за неравенством  будет выполняться
будет выполняться  .
.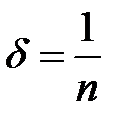 найдутся на отрезке
найдутся на отрезке 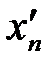 и
и 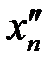 , что вслед за неравенством
, что вслед за неравенством 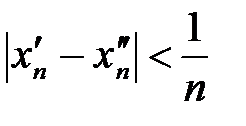 будет выполняться
будет выполняться 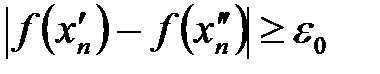 .
.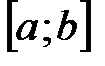 выделяются две ограниченные последовательности:
выделяются две ограниченные последовательности:
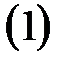

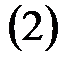
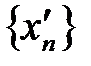 . Она ограничена, так как содержится на отрезке. По теореме Больцано-Вейерштрасса из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
. Она ограничена, так как содержится на отрезке. По теореме Больцано-Вейерштрасса из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.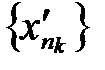 , сходящаяся к
, сходящаяся к 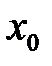 , т.е.
, т.е.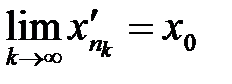 .
. .
.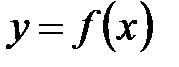 непрерывна на отрезке
непрерывна на отрезке 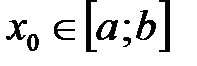 , т.е.
, т.е.
 .
. тоже будет сходится к
тоже будет сходится к  :
: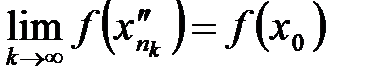 .
.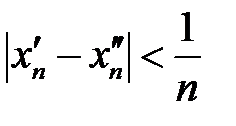 видно, что при
видно, что при 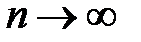 и другая подпоследовательность
и другая подпоследовательность 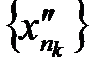 , выделенная из ограниченной последовательности
, выделенная из ограниченной последовательности 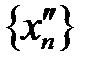 , тоже будет сходиться к
, тоже будет сходиться к 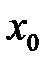 при
при  :
: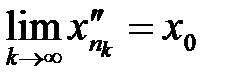 .
.
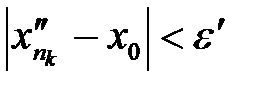

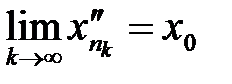 .
.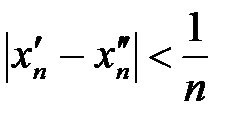 , то и
, то и 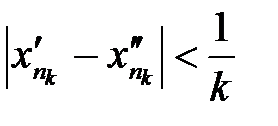 .
.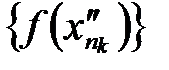 тоже будет сходиться к
тоже будет сходиться к 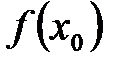 при
при 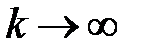 :
: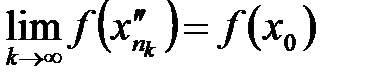 .
. :
: :
: 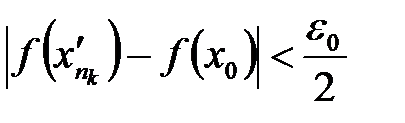 ;
;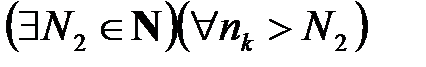 :
: 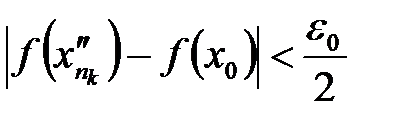 .
.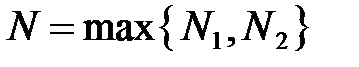 при
при 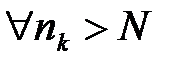 одновременно будут выполняться неравенства:
одновременно будут выполняться неравенства: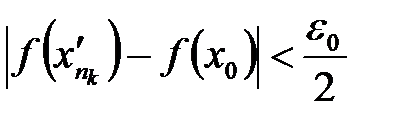
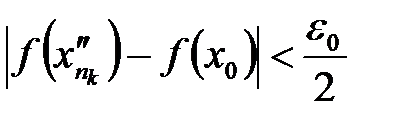 .
.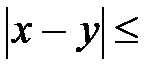
 , получим:
, получим: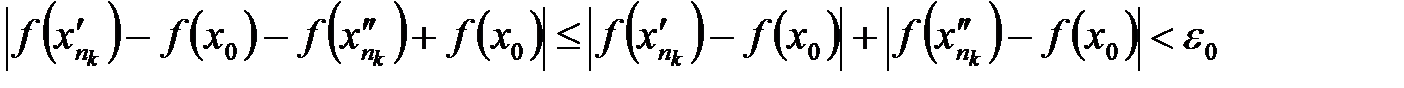
 для
для  .
. и
и 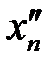 предполагалось, что
предполагалось, что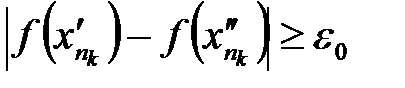 .
. Полученное противоречие показывает, что наше допущение, что функция
Полученное противоречие показывает, что наше допущение, что функция 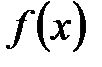 на отрезке
на отрезке 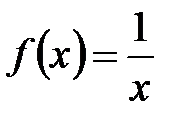 непрерывна на интервале
непрерывна на интервале 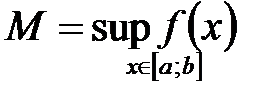 и
и  .
. (
(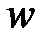 – разность между наибольшим и наименьшим значениями функции).
– разность между наибольшим и наименьшим значениями функции).


