
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Передаточных функций звеньев системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При исследовании и расчете систем автоматического управления исходят из математического описания происходящих в них физических процессов. Обычно это описание бывает представлено в виде системы дифференциальных уравнений, выражающих связи между переменными величинами и их производными. Такой подход, когда уравнения описывают поведение исследуемой системы в целом, является наиболее общим в математическом плане и применимым во всех случаях. Вместе с тем для большого класса систем автоматического управления (линейных систем) широко применяется и другой способ, связанный с использованием операторного метода. При этом способе исследуемая система разделяется на части — звенья направленного действия, обладающие свойством передачи сигнала только в одном направлении: от входа к выходу. Совокупность этих звеньев совместно с линиями связи между ними, характеризующими их взаимодействие, образует структурную схему системы управления. Между функциональными и структурными схемами есть определенная общность — те и другие отражают процесс передачи и переработки информации в замкнутом контура системы управления. Однако между ними существует и четкое различие: функциональные схемы характеризуют систему по составу входящих в нее элементов, рассматриваемых с точки зрения их назначения, т. е. выполняемых ими функций; структурные схемы, состоящие из звеньев направленного действия, описывают математически динамические свойства системы. Исходя из структуры системы и вида входящих в нее функциональных элементов, можно произвести разделение систем на звенья направленного действия в общем виде так, чтобы для каждого из них можно было наиболее просто определить передаточную функцию звена как отношение операторные изображений выходной величины звена к входной и соединить отдельные звенья между собой линиями связи. Передаточная функция каждого звена представляет собой записанное в операторной форме и разрешенное относительно изображения выходной величины дифференциальное уравнение данного звена. Таким образом, задача составления дифференциальных уравнений системы автоматического управления в целом сводится к составлению уравнений отдельных звеньев. Получаемый при этом выигрыш в части трудоемкости становится более очевидным, так как на практике в подавляющем большинстве случаев структурные схемы систем автоматического управления представляют собой различные комбинации небольшого числа так называемых типовых звеньев, передаточные функции и динамические свойства которых могут быть известны. Весьма важным преимуществом структурных схем является их физическая наглядность, дающая более ясное представление о процессах, происходящих в исследуемой системе, по сравнению с общей формой записи дифференциальных уравнений. На основе полученной функциональной схемы составим структурную схему системы и определим ее передаточные функции. Первым звеном можно считать преобразующий элемент - потенциометр П, входной величиной которого служит ошибка Q, а выходной - сигнал ошибки Uc, поступающий на вход усилителя. Так как это звено можно считать безынерционным, то его передаточная функция вырождается в передаточный коэффициент:
Вторым звеном, также безынерционным, будем считать усилитель с передаточным коэффициентом
где Uy— напряжение на управляющей обмотке двигателя. В качестве третьего звена примем асинхронный двигатель вместе с редуктором. Входной величиной этого звена является напряжение Uy. В качестве выходной величины принимают: 1) угол поворота выходной оси Qвых, являющийся выходной величиной следящей системы, или 2) угловую скорость вращения выходной оси Wвых, а затем добавляют отдельное интегрирующее звено, с помощью которого скорость вращения выходной оси преобразуется в угол поворота последней. Выберем второй вариант и запишем передаточную функцию третьего звена
а передаточную функцию последнего (интегрирующего) звена
При таком разделении следящей системы на звенья ее структурная схема примет вид, изображенный на рис. 3.
Рис. 3. Структурная схема следящей системы с асинхронным двухфазным двигателем
Передаточная функция разомкнутой системы, состоящей из последовательно включенных звеньев примет вид:
Передаточная функция для выходной величины следящей системы определяется по формуле:
Передаточная функция для ошибки имеет вид:
Учитывая, что передаточная функция двигателя может быть определена как:
где се - скоростной коэффициент двигателя, jp - передаточное число редуктора, Тм - электромеханическая постоянная времени, структурная схема системы имеет вид рис.4.
Рис.4. Структурная схема следящей системы с асинхронным двухфазным двигателем
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 568; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.126 (0.007 с.) |

 .
.





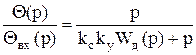 .
. ,
,



