
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электромагнитные свойства средыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ВВЕДЕНИЕ Практическое использование свойств электромагнитных колебаний началось с 1895 года, когда Попов А.С. обнародовал результаты своих исследований в области радио. Все последующие годы шло довольно интенсивное изучение и практическое применение этого открытия в различных отраслях науки и техники. В последнее десятилетие, как известно, взамен кабельных линий связи стали применять волоконно-оптические линии. В связи с этим в ряде высших учебных заведений связевого профиля открылись новые специальности. В ДВГУПС на факультете «Управление, автоматизация и телекоммуникации» открыли новую специализацию, где изучаются системы передачи информации с использованием волоконно-оптических линий. В настоящее время совершенно не издаётся литература (ни учебная, ни техническая) по названной теме. Это сильно затрудняется обучение студентов по новой специальности. Выпуск предлагаемого конспекта лекций поможет облегчить студентам изучение и освоение довольно сложного в математическом плане и практическом воплощении раздела учебной программы. Компьютерный набор текста осуществлен студентом факультета
ИСТОРИЧЕСКАЯ СПРАВКА Основным объектом изучения электродинамики является электромагнитное поле. Электромагнитное поле представляет собой особый вид материи. Главнейшие этапы развития теории и практики электродинамики следующие. В 1753 и в 1756 годах Ломоносов высказал мысль о динамической природе электричества, о связи между электрическими и световыми явлениями. В 1820 году Ампер исследовал влияние тока на ток, в 1831 году Фарадей открыл явление электромагнитной индукции. В 1873 году Максвелл опубликовал «Трактат об электричестве и магнетизме», где математически изложил основные законы электромагнитного поля. В 1888 году Герц дал метод решения уравнений Максвелла и экспериментально доказал возможность существования электромагнитных волн в пространстве. В 1895 году Попов осуществил первую в мире радиосвязь с помощью электромагнитных волн. В 1899 году Лебедев экспериментально доказал давление света, то есть электромагнитных волн, на тела. Энштейн в 1916 году высказал мысль об искривлении светового луча в поле тяготения, а Эддингтон в 1919 году измерил отклонение светового луча в гравитационном поле Солнца. В 1960 году Паунд взвесил световой луч. Электромагнитное поле является носителем энергии, способной преобразовываться в другие виды энергии, что широко используется в настоящее время.
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ Электрические заряды обусловливают электрические и магнитные явления, например, силовые взаимодействия между заряженными частицами и телами. Взаимодействие между заряженными частицами или телами осуществляется через электромагнитное поле. Электромагнитное поле определяется как особый вид материи, характеризующийся способностью распространяться в вакууме со скоростью, близкой к 3×108 м/с и оказывающий силовое воздействие на заряженные частицы. Электромагнитное поле представляет собой единство двух своих составляющих Графически структура векторного поля чаще всего изображается с помощью линий поля, которые являются касательными к векторам поля в каждой точке пространства. Плотность этих линий пропорциональна величине вектора в данной точке. Векторы поля D и Н – это функции источников. Вектор электрического смещения D,
где Вектор напряженности магнитного поля Н,
Векторы Е и В являются силовыми характеристиками электромагнитного поля. Эта сила является суперпозицией сил, создаваемых электрической и магнитной составляющими поля:
где
Вектор магнитной индукции можно определить из соотношения
Размерность вектора В находится как отношение Уравнения Максвелла Макроскопическая теория электромагнетизма основывается на уравнениях Максвелла. Система уравнений электромагнитного поля была постулированна Максвеллом, т.е. введена в теорию аксиоматически. Исходными из этих уравнений являются уравнения Максвелла в интегральной форме, как непосредственно основанные на опыте.
Циркуляция магнитного поля Циркуляция вектора напряженности магнитного поля
где Таким образом, можно записать: Если циркуляция вектора
Так как площадка S может быть ориентированна в любом направлении, то Итак, ротор вектора напряженности магнитного поля в любой его точке равен сумме плотности истинного электрического тока и скорости изменения вектора электрического смещения в этой точке. Таким образом, магнитное поле создается при любом движении электрических зарядов (электрическом токе) и изменении во времени вектора электрического смещения.
Граничные условия На границе между материалами (телами) параметры среды Для решения задач электродинамики, кроме уравнений Максвелла, необходимо знать граничные условия – соотношения между векторами, находящимся по обе стороны раздела сред. Можно показать, что нормальная составляющая вектора электрической индукции D при переходе через граничную поверхность претерпевает скачок, численно равный поверхностной плотности электрического заряда:
Поверхностный заряд образуется на поверхности проводников лишь в электрическом поле. В переменном поле такие заряды могут возникнуть только на поверхности идеального проводника. Поэтому при переменных полях в реальных средах нормальная составляющая вектора магнитной индукции на границе не изменяется. Такое же заключение можно сделать относительно нормальной составляющей вектора магнитной индукции: при переходе через границу он не изменяется. Относительно касательных составляющих полей можно теоретически доказать, что касательная составляющая вектора напряженности магнитного поля непрерывна на границе любых реальных сред. То же относится и к электрической составляющей (касательной).
Идеального проводника В электростатике при любой проводимости материала электрические поля в нем отсутствуют. Переменные же поля проникают в материал с конечной проводимостью. Однако если проводник считать идеальным, то заряды внутри него столь подвижны, что мгновенно реагируют на сколь угодно быстрое изменение поля, создавая на его поверхности поверхностную плотность заряда:
здесь Аналогично при изменении во времени магнитного поля поверхностные заряды перемещаются и создают поверхностный ток
где Итак, в идеально проводящей среде электромагнитное поле отсутствует:
Тангенциальная составляющая напряженности электрического поля и нормальная составляющая напряженности магнитного поля у поверхности идеального проводника отсутствуют. Нормальная составляющая электрического поля определяется распределением поверхностного заряда. Плотность электрического тока на поверхности равна величине и перпендикулярна по направлению касательной составляющей напряженности магнитного поля у поверхности. Комплексные проницаемости Электрические потери. Электрическое поле вызывает два вида потерь в среде. Это, во-первых, потери обусловленные проводимостью материала. Во-вторых, это поляризационные (диэлектрические) потери, которые объясняются трением при смещении заряженных частиц вещества в переменном поле. Это ведет к отставанию вектора
где Магнитные потери. В магнитных материалах при перемагничивании также возникают потери на трение, в результате которых вектор
Волны в диэлектрике Диэлектрик характеризуется комплексной диэлектрической проницаемостью:
Определим составляющие коэффициента распространения используя малость
Так как для степенного ряда
где В вакууме он равен Фазовая скорость электромагнитной волны в вакууме (т.е. скорость света) определяется выражением:
Фазовую скорость волны в любом диэлектрике можно определить по формуле:
Длина волны в среде зависит от ее параметров:
Частота колебаний в среде не меняется. Волновое сопротивление вакуума
Модуль волнового сопротивления диэлектрической среды:
Волны в проводнике Среда считается проводником, если
Эта величина на высоких частотах не превышает долей миллиметра. Закон изменения напряженности поля представляет экспоненту На глубине, равной длине волны, поле убывает в 535 раз, а мощность примерно в 300 тысяч раз. Поэтому металлы нельзя применять как среду для передачи электромагнитных волн.
ТЕОРЕМА ЕДИНСТВЕННОСТИ Энергия представляет собой количественную меру движения материи. Закон сохранения энергии – один из фундаментальных законов природы, которому подчиняется явление электромагнетизма. Электромагнитное поле подчиняется закону сохранения массы:
Макроскопическая теория поля основана (кроме уравнений Максвелла) на следующих двух предположениях. 1. Электромагнитная энергия распределена в пространстве с объемной плотностью v,
2. Плотность потока электромагнитной энергии
где
Она может изменяться во времени вследствие: - перехода внутри объема - приобретения полем внутри объема V энергии от сторонних источников. Скорость увеличения энергии поля равна мощности сторонних сил - излучения электромагнитных волн путем перехода их из одного объема V через ограничивающую поверхность S. Эта мощность определяется соотношением:
Между названными составляющими существует баланс энергии (по закону сохранения энергии):
Закон сохранения энергии можно представить в интегральной форме:
где v – объемная плотность энергии, находящейся в объеме; Рn – объемная плотность мощности потерь; Этот же закон в дифференциальной форме:
Объемная плотность мощности потерь:
Поле отдает энергию, если угол между
Это есть закон Джоуля-Ленца в дифференциальной форме. После интегрирования получим известную формулировку закона Ома:
Если сторонний ток по отношению к В соответствии со сказанным объемная плотность мощности сторонних сил:
Теорема Пойтинга Теорема Пойтинга устанавливает соответствие баланса электромагнитной энергии (см. п. 1.7) системе уравнений Максвелла. Произведем с уравнениями Максвелла в дифференциальной форме некоторые преобразования. Умножим почленно второе уравнение скалярно на
Это и есть уравнение Пойтинга в дифференциальной форме. Вычислим скорость электромагнитной волны как скорость переноса энергии и массы поля (рис. 5).
Найти: Решение: за время
откуда энергетическая скорость электромагнитной волны определится как
Выполняя те же операции с уравнениями Максвелла в комплексной форме, получим выражение:
где Последнее уравнение есть уравнение Пойтинга в комплексной форме. В процессе распространения волны электрическая энергия непрерывно переходит в магнитную и обратно. Поскольку существует равновесие электрического и магнитного полей в распространяющейся волне, то для скорости распространения волны можно получить следующее соотношение:
Сравнивая полученное выражение с выражением для фазовой скорости волны, получаем важный вывод: в диэлектрике с малыми потерями энергетическая скорость волны совпадает по величине и направлению с ее фазовой скоростью. Теорема единственности Методы решения задач электродинамики, основанные на рассмотренных выше уравнениях, могут быть различными. Однако решение, полученное каким-либо способом, единственно, т.е. электромагнитное поле определяется однозначно по заданному распределению источников. Рассмотрим внутреннюю и внешнюю задачи. Для области пространства, ограниченной поверхностью S верна следующая теорема. Монохроматическое электромагнитное поле в определенной ограниченной области V определится однозначно, если: - в каждой точке области среда обладает электрическими либо магнитными потерями ( - заданы источники в этой области; - заданы значения тангенциальной составляющей электрического или магнитного вектора на границе этой области. Очевидно, что при отсутствии потерь в среде возможно существование свободных незатухающих колебаний, не связанных с источниками. В этом случае решение внутренней задачи становится неоднозначным. Внешняя задача. Пусть рассматриваемое пространство неограниченно, т.е. внешней границы S не существует. Это эквивалентно сфере с бесконечно большим радиусом. В этом случае монохроматическое поле определяется в безграничной области однозначно, если: - в каждой точке пространства среда обладает либо электрическими, либо магнитными потерями; - заданы источники в этой области; - заданы значения тангенциальной составляющей электрического или магнитного вектора на внутренней границе области; - все источники находятся на конечном расстоянии от начала координат; - поля убывают на бесконечности быстрее, чем Первые три условия совпадают с соответствующими условиями для внутренней задачи. Таким образом, найденные любым способом решение корректно поставленной задачи отвечает действительному распределению поля, и никакого другого решения быть не может.
Идеальных диэлектриков Полное прохождение. Для волн с параллельной поляризацией существует угол падения, именуемый углом Брюстера В соответствии с законом преломления (Снеллиуса):
Этот угол называют также углом полной поляризации. Для перпендикулярной поляризации не существует такого угла. Вышеназванное свойство имеет большое практическое применение. Примеры. 1. Если волна с произвольной поляризацией на диэлектрическую пластину под углом Брюстера 2. Диэлектрические пластины и шайбы, служащие для герметизации в различных устройствах, ставят под углом Брюстера. Тогда они полностью прозрачны для проходящих волн. Полное отражение. Рассмотрим случай, когда волна проходит из среды оптически более плотной в менее плотную ( Из приведенного ранее закона Снеллиуса
получим: Критическим углом называется угол:
Самым характерным примером использования явления полного отражения является оптический кабель (волновод), показанный на рис. 9.
Электрического вибратора Известно, что мощность излучения можно определить по формуле:
Подынтегральное выражение не зависит от азимутального угла
Поэтому: Сравним с выражением: Следовательно, часть выражения перед
Видим, что чем больше RS, тем больше излучаемая мощность.
4.2. Инвариантность уравнений поля к элементам электрических И магнитных полей В теории электромагнитных полей (электродинамике) доказывается, что, не изменяя уравнений Максвелла, можно заменить все электрические величины магнитными, а магнитные электрическими при соблюдении определенных правил знаков. Правила замен можно свести вместе в следующую таблицу:
В этом случае вводится понятие магнитного излучателя и вместо электрического тока действует магнитный ток. Подобны также диаграммы направленности. В поле магнитного вибратора Е и Н меняются местами. Мощность излучения элементарного магнитного вибратора вычисляется по формуле:
Проводимость излучения из этой формулы:
Примерами магнитного излучателя могут служить катушка с током (с сердечником или без него) или щель в плоской проводящей поверхности. Чаще всего размеры (длина) щели равны
ВОЛНОВОДЫ И РЕЗОНАТОРЫ Основные сведения. Электромагнитная волна в устройствах и системах связи должна распространяться по определенному пути и достигать пункта назначения с наименьшими потерями. Эту функцию выполняют направляющие системы; их называют также линиями передачи или волноводами. Направляющие системы должны удовлетворять следующим требованиям: - малое затухание; - обеспечение заданной передаваемой мощности, что связано с недопустимостью электрического пробоя; - экономическая целесообразность (малый вес, доступные материалы, простота конструкции и технологии производства). Применяются следующие конструкции направляющих систем: - двухпроводные линии (килогерцы); - коаксиальный кабель (мегагерцы); - линии поверхностной волны (мегагерцы – гигагерцы); - металлические волноводы (оптические волокна), (терагерцы).
Классы волн Е и Н Эти волны имеют одну продольную составляющую Е-волны, или «электрические», имеют электрическую продольную составляющую и, естественно, поперечные компоненты E и H. Другое их название ТМ-волны. Н-волны, или «магнитные» имеют продольную магнитную составляющую
Круглый волновод Довольно часто наряду с прямоугольными волноводами применяют круглые волноводы. Здесь основной волной является волна Картина поля волны
Рис. 16
Для сравнения приведем картину поля волны
Рис. 17
Режимы волны По направляющей системе могут распространяться волны либо одного, либо нескольких типов волн. В первом случае эту систему называют одномодовой, во втором – многомодовой. В частности, одномодовый режим характерен для двухпроводной линии с ТЕМ-волной в широком диапазоне частот. Если на конце одномодовой направляющей системы включена нагрузка, то, кроме падающей волны с амплитудой
При движении вдоль линии амплитуда и фаза волны меняются по закону
а отраженной по закону:
Коэффициент отражения в произвольном сечении двух встречно бегущих волн равен
В линии без потерь модуль Суперпозиция двух встречных волн создает в линии стоячую волну. Параметры нагрузки и режим волны в линии можно охарактеризовать комплексным коэффициентом отражения или комплексным нормированным сопротивлением. Нормированная волна – это волна, несущая мощность в 1 Вт. Режим работы линии можно характеризовать коэффициентом стоячей волны
Существует также такая связь между этими коэффициентами, где модуль коэффициента отражения равен
В общем случае в линии устанавливается режим смешанной волны. Чисто стоячая волна возникает в случае равенства по модулю амплитуд отраженной и падающей волн ( Режим бегущей волны устанавливается при полном отсутствии отраженной волны.
ВОЗБУЖДЕНИЕ ВОЛНОВОДОВ Возбуждением волноводов называется создание в нем высокочастотного электромагнитного поля. Устройство, служащее для этой цели, называют элементом связи или возбудителем. В основном используют следующие способы возбуждения волноводов: - с помощью штыря; - петли связи; - щели в стенке волновода; - отверстия (чаще всего круглого). При возбуждении решается задача возбудить определенный тип волн, не допуская нежелательного типа. Доказано, что амплитуда возбужденной волны максимальна, если: - сторонний электрический ток протекает вдоль электромагнитного поля возбужденной волны, т.е. ось штыря располагается параллельно Е; - сторонний магнитный ток – вдоль магнитного поля (ось петли или осевая линия щели параллельны вектору Н); - возбудитель располагается в максимуме соответствующего компонента поля. Отметим, что элемент связи, обеспечивающий эффективную передачу мощности в волновод, согласно теореме взаимности, будет столь же эффективно принимать мощность от волны того же типа и передавать ее в смежную линию.
Запредельные волноводы В запредельных волноводах волновые процессы невозможны. Имеется только затухающее, чисто реактивное поле, экспоненциально убывающее при удалении от возбудителя. При
Коаксиальные линии В коаксиальных кабелях распространяется волна типа ТЕМ. Частотный диапазон (до» 100 МГц), который зависит от конструкции радиочастотных кабелей и мощности волны в кабеле. Уязвимое место – граница на поверхности внутри диэлектрика. Это опасное место с точки зрения пробоя. Пробивное напряжение:
где Применение коаксиальных кабелей: - гибкие кабели небольшой длины применяют в радиоэлектронной аппаратуре для соединения отдельных блоков и внутриблочных соединений до частот 10 ГГц; - антенные фидеры используют до частот в сотни МГц; - на магистральных линиях связи для передачи сигналов телевидения и многоканальной телефонии – до частот в 10 МГц. Иногда конструктивно объединяют несколько коаксиальных линий.
Полосковые линии
Широкие пластины соединяются между собой и с землей. Поэтому экранирование получается достаточно хорошим. Если в качестве диэлектрика используется воздух, то потери в таком волноводе значительно меньше. В таких линиях устанавливается волна типа ТЕМ.
ОБЪЕМНЫЕ РЕЗОНАТОРЫ Резонатор – это колебательная система, используемая в сантиметровом и дециметровом диапазонах. Постепенное превращение колебательной системы в виде контура в резонатор показано на рис. 19.
Рис. 19
Как любой контур, объемный резонатор характеризуется резонансной частотой, добротностью, полосой пропускания. В зависимости от типа колебаний резонатора он характеризуется несколькими резонансными частотами. Добротность можно определить следующим образом
до
|
||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 604; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.67.248 (0.011 с.) |

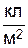 , равен
, равен ,
, – орт, направленный вдоль радиус-вектора.
– орт, направленный вдоль радиус-вектора. , характеризует связь электрического тока с собственным магнитным полем:
, характеризует связь электрического тока с собственным магнитным полем:
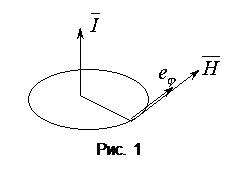 где
где  – орт в цилиндрической системе координат, у которой ось z совпадает с направлением тока (см. рис. 1).
– орт в цилиндрической системе координат, у которой ось z совпадает с направлением тока (см. рис. 1).

 ,
, – вектор скорости движения заряда. Отсюда вектор напряженности электрического поля Е,
– вектор скорости движения заряда. Отсюда вектор напряженности электрического поля Е,  ,
, .
. .
. (тесла).
(тесла).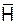 по любому замкнутому контуру (магнитодвижущая сила) равна сумме истинного электрического тока и тока смещения, протекающего сквозь поверхность, ограничивающую этим контуром:
по любому замкнутому контуру (магнитодвижущая сила) равна сумме истинного электрического тока и тока смещения, протекающего сквозь поверхность, ограничивающую этим контуром: ,
, – истинный электрический ток (ток проводимости), а также конвекционный ток;
– истинный электрический ток (ток проводимости), а также конвекционный ток;  – скорость изменения потока электрического смещения (ток смещения).
– скорость изменения потока электрического смещения (ток смещения). . Это есть обобщенный закон Ампера (в интегральной форме).
. Это есть обобщенный закон Ампера (в интегральной форме). отличен от нуля. Считая
отличен от нуля. Считая  .
. (дифференциальная форма закона Ампера).
(дифференциальная форма закона Ампера). скачкообразно изменяются. При этом неизбежно испытывают скачки некоторые векторы поля.
скачкообразно изменяются. При этом неизбежно испытывают скачки некоторые векторы поля.
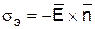 ,
,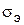 – поверхностная плотность заряда, которая обеспечивает нулевое электрическое поле внутри проводника.
– поверхностная плотность заряда, которая обеспечивает нулевое электрическое поле внутри проводника.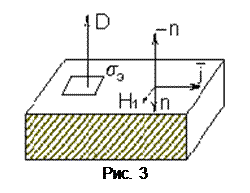
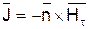 ,
,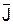 – плотность поверхностного тока на поверхности идеального проводника, благодаря чему магнитное поле внутри проводника отсутствует.
– плотность поверхностного тока на поверхности идеального проводника, благодаря чему магнитное поле внутри проводника отсутствует.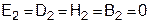 (рис. 3). Таким образом, получаем для изотропной среды:
(рис. 3). Таким образом, получаем для изотропной среды: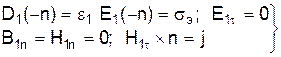
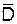 от вектора
от вектора 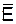 . Следовательно, диэлектрическая проницаемость есть комплексная величина:
. Следовательно, диэлектрическая проницаемость есть комплексная величина: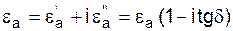 ,
,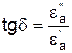 – тангенс угла диэлектрических потерь. В широкой полосе частот
– тангенс угла диэлектрических потерь. В широкой полосе частот 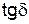 постоянен (до»100 ГГц).
постоянен (до»100 ГГц).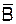 отстает по фазе от вектора
отстает по фазе от вектора 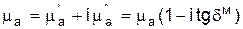 .
. .
. .
. верно приблизительное выражение
верно приблизительное выражение  , то воспользовавшись разложением в степенной ряд получим:
, то воспользовавшись разложением в степенной ряд получим: ,
, – коэффициент распространения,
– коэффициент распространения,  – волновое число (фазовый коэффициент) в идеальном диэлектрике (т.е. без потерь). В реальном диэлектрике с малыми потерями он определяется по той же формуле. Таким образом, для реального диэлектрика с малыми потерями фазовый коэффициент
– волновое число (фазовый коэффициент) в идеальном диэлектрике (т.е. без потерь). В реальном диэлектрике с малыми потерями он определяется по той же формуле. Таким образом, для реального диэлектрика с малыми потерями фазовый коэффициент 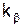 равен волновому числу
равен волновому числу  .
. .
. .
. .
. .
. , Ом, вычисляется по формуле
, Ом, вычисляется по формуле .
. .
. . Электромагнитная волна проникает в проводник на очень небольшую глубину, называемую скин-слоем:
. Электромагнитная волна проникает в проводник на очень небольшую глубину, называемую скин-слоем:
 .
. .
.
 .
. ,
, 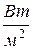 , равна векторному произведению напряженности электрического и магнитного полей:
, равна векторному произведению напряженности электрического и магнитного полей:
 , определяется объемным интегралом:
, определяется объемным интегралом: .
. ;
; .
. .
. ,
, – объемная плотность мощности сторонних сил.
– объемная плотность мощности сторонних сил. .
. , так как
, так как  .
.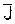 и
и  меньше
меньше  . Ток проводимости
. Ток проводимости  , тогда
, тогда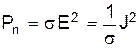 .
. .
. .
. , а первое – на
, а первое – на 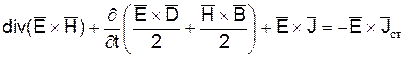 .
. Дано:
Дано:  – плотность потока энергии; v – объемная плотность энергии волны.
– плотность потока энергии; v – объемная плотность энергии волны. – энергетическую скорость электромагнитной волны.
– энергетическую скорость электромагнитной волны. энергия
энергия 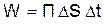 заполняет объем
заполняет объем  , где
, где 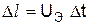 .
. 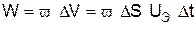 . Приравнивая оба выражения для
. Приравнивая оба выражения для  получим:
получим: ,
, .
.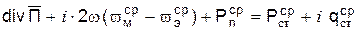 ,
, – мнимая часть сторонней мощности (символ «
– мнимая часть сторонней мощности (символ « » означает усреднение за период).
» означает усреднение за период). .
. ); величина этих потерь может быть весьма мала;
); величина этих потерь может быть весьма мала; .
. , при котором отраженная волна отсутствует, т.е. волна полностью переходит во вторую среду.
, при котором отраженная волна отсутствует, т.е. волна полностью переходит во вторую среду. ;
; 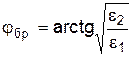 .
. , то отраженная волна имеет только перпендикулярную поляризацию, т.к. параллельно поляризованная компонента беспрепятственно проходит через пластину.
, то отраженная волна имеет только перпендикулярную поляризацию, т.к. параллельно поляризованная компонента беспрепятственно проходит через пластину. ) при малых потерях в обеих средах.
) при малых потерях в обеих средах.
 .
. .
. При превышении этого угла волна будет полностью отражаться от поверхности раздела сред.
При превышении этого угла волна будет полностью отражаться от поверхности раздела сред. .
. и интегрирование по нему дает
и интегрирование по нему дает  . Интегрирование по
. Интегрирование по  приводит к результату:
приводит к результату: .
. .
.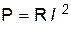 .
. есть некое сопротивление, оно называется сопротивлением излучения RS, Ом:
есть некое сопротивление, оно называется сопротивлением излучения RS, Ом: .
.



 .
. .
. .
. или
или  .
. , где есть одна вариация по радиусу и одна вариация по углу
, где есть одна вариация по радиусу и одна вариация по углу 
 (рис. 17).
(рис. 17).
 , может возникнуть отраженная волна
, может возникнуть отраженная волна 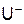 . Коэффициент отражения нагрузки
. Коэффициент отражения нагрузки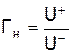 .
. ,
, .
. .
.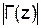 одинаков в любом сечении.
одинаков в любом сечении. или коэффициентом бегущей волны
или коэффициентом бегущей волны  :
: ;
; .
. .
. ). Тогда
). Тогда  ,
,  ;
;  ,
,  .
. волноводы используются в качестве аттенюаторов, т.е. устройств, ослабляющих на определенную величину мощность волны в линии передачи.
волноводы используются в качестве аттенюаторов, т.е. устройств, ослабляющих на определенную величину мощность волны в линии передачи. ,
, – пробивная напряженность поля в диэлектрике кабеля.
– пробивная напряженность поля в диэлектрике кабеля. Полосковые (или ленточные) линии получили широкое распространение в связи с внедрением в технику сверхвысоких частот технологии печатных плат. Они используются преимущественно в сантиметровом и дециметровом диапазонах волн. Их изготавливают на основе диэлектрических пластин, покрытых металлической фольгой толщиной 10–100 мкм. В качестве диэлектрика используют фторопласт, стирофлекс и другие высокочастотные диэлектрики (рис. 18).
Полосковые (или ленточные) линии получили широкое распространение в связи с внедрением в технику сверхвысоких частот технологии печатных плат. Они используются преимущественно в сантиметровом и дециметровом диапазонах волн. Их изготавливают на основе диэлектрических пластин, покрытых металлической фольгой толщиной 10–100 мкм. В качестве диэлектрика используют фторопласт, стирофлекс и другие высокочастотные диэлектрики (рис. 18).
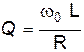 ,
,


