
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Излучение и дифракция электромагнитного поляСодержание книги
Поиск на нашем сайте На практике приходится решать две противоположные задачи: проектировать излучающие устройства, которые должны излучать по возможности всю подводимую к ним энергию, и создавать направляющие устройства, которые должны только передавать электромагнитные волны, не излучая их за пределы этого устройства. Очевидно, что обе задачи сводятся к определению во всем пространстве электромагнитного поля, созданного некоторым распределением сторонних токов. В качестве исходной примем систему уравнений Максвелла для однородной изотропной среды в комплексной форме. Для решения поставленных задач вводится понятие векторного потенциала магнитного поля
(равноценное название – электродинамический потенциал). Вводится также понятие скалярного электродинамического потенциала:
Здесь скаляр В результате решения названных уравнений Максвелла получаем неоднородное волновое уравнение для векторного электродинамического потенциала:
и для скалярного электродинамического потенциала соответственно:
Здесь
Используя введенное понятие электродинамического потенциала, с помощью первого уравнения Максвелла в комплексной форме находим напряженность электрического поля:
В качестве стороннего источника обычно рассматривают элементарный электрический диполь, который представляет собой отрезок линейного проводника с неизменным по длине переменным током Определим электромагнитное поле, создаваемое таким элементарным излучателем, помещенным в среду с малыми потерями
Получим следующее выражение:
где
Видим, что относительный вес отдельных слагаемых меняется в функции от Различают в связи с этим три зоны в поле получателя: ближнюю Будем считать среду слабопоглощающей, т.е. Поле в ближней зоне. Здесь основную роль играют высшие степени
Поле в промежуточной зоне имеет сложную структуру, где все составляющие играют определенную роль. Поле в дальней зоне представляет наибольший интерес; здесь
где Общие для всех зон закономерности: - осевая симметрия; - ортогональность электрического и магнитного векторов; - пропорциональность всех составляющих моменту тока
|
||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

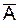 (с размерностью
(с размерностью 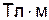 ):
):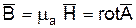
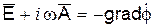 или
или  .
.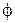 – и есть вновь введенное понятие.
– и есть вновь введенное понятие.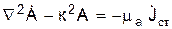
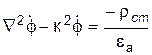 .
.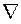 – Лапласиан (оператор Лапласа):
– Лапласиан (оператор Лапласа):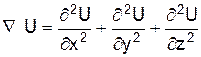 .
. .
.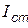 . Диполь имеет длину
. Диполь имеет длину  и поперечные размеры значительно меньше длины волны (вибратор Герца).
и поперечные размеры значительно меньше длины волны (вибратор Герца).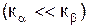 .
.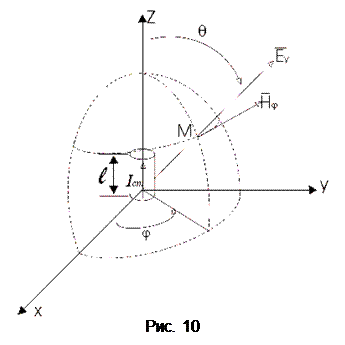 Используя вышеприведенную формулу, определим напряженность электрической составляющей. При этом будем считать, что присутствуют в полярных координатах только две составляющие поля
Используя вышеприведенную формулу, определим напряженность электрической составляющей. При этом будем считать, что присутствуют в полярных координатах только две составляющие поля 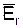 и
и 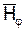 (рис. 10).
(рис. 10).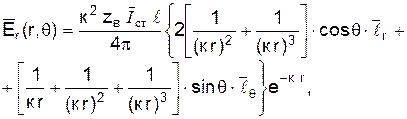
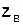 – волновое сопротивление среды.
– волновое сопротивление среды.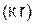 , что приводит к качественным различиям поля.
, что приводит к качественным различиям поля.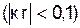 , промежуточную
, промежуточную 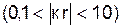 и дальнюю
и дальнюю 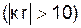 .
. .
.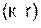 , тогда
, тогда .
.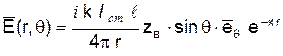 ,
, – волновое число,
– волновое число,  – коэффициент распространения,
– коэффициент распространения, 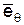 – единичный орт. Напомним, что
– единичный орт. Напомним, что 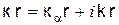 .
.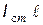 .
.


