
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поток электрического смещенияСодержание книги
Поиск на нашем сайте Обобщенная теорема Гаусса – интегральная форма уравнений Максвелла: поток электрического смещения через любую замкнутую поверхность равен электрическому заряду, заключенному внутри этой поверхности, т.е.
Отсюда следует, что, если внутри указанной поверхности нет зарядов, то поток электрического смещения через эту поверхность равен нулю. Следствием теоремы Гаусса является закон Кулона:
где Связь между объемной плотностью электрического заряда и вектором электрического смещения устанавливается обобщенной теоремой Гаусса в дифференциальной форме. Будем сжимать поверхность S вокруг избранной точки так, чтобы заключенный внутри ее объем стремился к нулю. Эта операция математически запишется следующим образом:
Левая часть уравнения есть дивергенция вектора (или расходимость), т.е. можно записать:
Дивергенция и ротор векторного поля Дивергенцией или расхождением поля Д называется скаляр, определенный в каждой точке поля и являющийся объемной производной этого поля:
Вычисляется по формуле:
Ротор (иначе ротация) поля D есть вектор, определенный в каждой точке поля и являющийся объемной производной этого поля, взятой с обратным знаком:
По другому определению ротацией поля Д называется вектор, образуемый следующим образом (см. рис. 2): 1) через точку r проводят небольшую площадку S; 2) вычисляют циркуляцию 3) рассматривают отношение этой циркуляции к площади S, когда S стремится к нулю, стягиваясь к точке r, причем положение площади остается неизменным; 4) изменяя положение этой площадки, устанавливают направление, при котором полученный предел достигает максимума; 5)
Формула для вычисления в декартовых координатах имеет следующее выражение
Таким образом, в каждой точке поля дивергенция вектора D равна объемной плотности электрического заряда.
Циркуляция магнитного поля Циркуляция вектора напряженности магнитного поля
где Таким образом, можно записать: Если циркуляция вектора
Так как площадка S может быть ориентированна в любом направлении, то Итак, ротор вектора напряженности магнитного поля в любой его точке равен сумме плотности истинного электрического тока и скорости изменения вектора электрического смещения в этой точке. Таким образом, магнитное поле создается при любом движении электрических зарядов (электрическом токе) и изменении во времени вектора электрического смещения.
|
||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 484; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

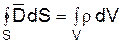 .
. ,
, – единичный орт,
– единичный орт,  и
и 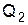 – величины зарядов, r – расстояние между зарядами.
– величины зарядов, r – расстояние между зарядами.
 .
.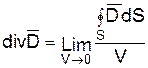 .
. (в декартовых координатах).
(в декартовых координатах).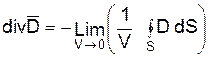 .
. вдоль контура, ограничивающего эту площадку;
вдоль контура, ограничивающего эту площадку; в точке r определяется вектор
в точке r определяется вектор  , модуль которого равен полученному максимуму, а направление совпадает с направлением вектора площадки Smax, т.е.
, модуль которого равен полученному максимуму, а направление совпадает с направлением вектора площадки Smax, т.е.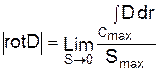 .
. .
.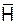 по любому замкнутому контуру (магнитодвижущая сила) равна сумме истинного электрического тока и тока смещения, протекающего сквозь поверхность, ограничивающую этим контуром:
по любому замкнутому контуру (магнитодвижущая сила) равна сумме истинного электрического тока и тока смещения, протекающего сквозь поверхность, ограничивающую этим контуром: ,
, – истинный электрический ток (ток проводимости), а также конвекционный ток;
– истинный электрический ток (ток проводимости), а также конвекционный ток;  – скорость изменения потока электрического смещения (ток смещения).
– скорость изменения потока электрического смещения (ток смещения). . Это есть обобщенный закон Ампера (в интегральной форме).
. Это есть обобщенный закон Ампера (в интегральной форме). отличен от нуля. Считая
отличен от нуля. Считая  .
. (дифференциальная форма закона Ампера).
(дифференциальная форма закона Ампера).


