
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электромагнитная индукция. Закон ФарадеяСодержание книги
Поиск на нашем сайте Интегральная форма. Циркуляция вектора напряженности электрического поля Е по любому замкнутому контуру равна скорости изменения магнитного потока, пронизывающего этот контур, с обратным знаком в правой системе координат:
где Дифференциальная форма. Ротор вектора напряженности электрического поля в любой его точке равен по величине и противоположен по знаку скорости изменения вектора магнитной индукции в этой точке, т.е.
Известно, что поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. Линии вектора В замкнуты либо уходят в бесконечность. Известно также, что магнитные заряды в природе отсутствуют.
Основные уравнения электромагнитного поля Сведем вместе основные законы макроскопической электродинамики в неподвижных средах, которые вкратце были рассмотрены ранее. Уравнения Максвелла в интегральной форме:
Уравнения Максвелла в дифференциальной форме:
Первое уравнение системы представляет собой обобщенный закон Ампера, второе – обобщенный закон Фарадея, третье – обобщенную теорему Гаусса, четвертое отображает соленоидальность поля магнитной индукции. Материальные уравнения для изотропных сред:
Уравнение силы Лоренца: Уравнения Максвелла в дифференциальной форме составляют основу всей электродинамики. Известно, что переменные электрические и магнитные поля не существуют независимо друг от друга, они непрерывно переходят одно в другое и образуют электромагнитную волну. Интегральные уравнения остаются справедливыми даже в том случае, если входящие в них поверхности и контуры пересекают границы, где физические свойства среды резко изменяются.
Граничные условия На границе между материалами (телами) параметры среды Для решения задач электродинамики, кроме уравнений Максвелла, необходимо знать граничные условия – соотношения между векторами, находящимся по обе стороны раздела сред. Можно показать, что нормальная составляющая вектора электрической индукции D при переходе через граничную поверхность претерпевает скачок, численно равный поверхностной плотности электрического заряда:
Поверхностный заряд образуется на поверхности проводников лишь в электрическом поле. В переменном поле такие заряды могут возникнуть только на поверхности идеального проводника. Поэтому при переменных полях в реальных средах нормальная составляющая вектора магнитной индукции на границе не изменяется. Такое же заключение можно сделать относительно нормальной составляющей вектора магнитной индукции: при переходе через границу он не изменяется. Относительно касательных составляющих полей можно теоретически доказать, что касательная составляющая вектора напряженности магнитного поля непрерывна на границе любых реальных сред. То же относится и к электрической составляющей (касательной).
|
||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 или
или  ,
, – электродвижущая сила,
– электродвижущая сила,  – магнитный поток или поток вектора магнитной индукции.
– магнитный поток или поток вектора магнитной индукции. .
.

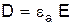 ;
;  ;
; 
 .
.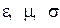 скачкообразно изменяются. При этом неизбежно испытывают скачки некоторые векторы поля.
скачкообразно изменяются. При этом неизбежно испытывают скачки некоторые векторы поля.



