
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергия электромагнитного поля.Содержание книги
Поиск на нашем сайте ТЕОРЕМА ЕДИНСТВЕННОСТИ Энергия представляет собой количественную меру движения материи. Закон сохранения энергии – один из фундаментальных законов природы, которому подчиняется явление электромагнетизма. Электромагнитное поле подчиняется закону сохранения массы:
Макроскопическая теория поля основана (кроме уравнений Максвелла) на следующих двух предположениях. 1. Электромагнитная энергия распределена в пространстве с объемной плотностью v,
2. Плотность потока электромагнитной энергии
где
Она может изменяться во времени вследствие: - перехода внутри объема - приобретения полем внутри объема V энергии от сторонних источников. Скорость увеличения энергии поля равна мощности сторонних сил - излучения электромагнитных волн путем перехода их из одного объема V через ограничивающую поверхность S. Эта мощность определяется соотношением:
Между названными составляющими существует баланс энергии (по закону сохранения энергии):
Закон сохранения энергии можно представить в интегральной форме:
где v – объемная плотность энергии, находящейся в объеме; Рn – объемная плотность мощности потерь; Этот же закон в дифференциальной форме:
Объемная плотность мощности потерь:
Поле отдает энергию, если угол между
Это есть закон Джоуля-Ленца в дифференциальной форме. После интегрирования получим известную формулировку закона Ома:
Если сторонний ток по отношению к В соответствии со сказанным объемная плотность мощности сторонних сил:
Теорема Пойтинга Теорема Пойтинга устанавливает соответствие баланса электромагнитной энергии (см. п. 1.7) системе уравнений Максвелла. Произведем с уравнениями Максвелла в дифференциальной форме некоторые преобразования. Умножим почленно второе уравнение скалярно на
Это и есть уравнение Пойтинга в дифференциальной форме. Вычислим скорость электромагнитной волны как скорость переноса энергии и массы поля (рис. 5).
Найти: Решение: за время
откуда энергетическая скорость электромагнитной волны определится как
Выполняя те же операции с уравнениями Максвелла в комплексной форме, получим выражение:
где Последнее уравнение есть уравнение Пойтинга в комплексной форме. В процессе распространения волны электрическая энергия непрерывно переходит в магнитную и обратно. Поскольку существует равновесие электрического и магнитного полей в распространяющейся волне, то для скорости распространения волны можно получить следующее соотношение:
Сравнивая полученное выражение с выражением для фазовой скорости волны, получаем важный вывод: в диэлектрике с малыми потерями энергетическая скорость волны совпадает по величине и направлению с ее фазовой скоростью. Теорема единственности Методы решения задач электродинамики, основанные на рассмотренных выше уравнениях, могут быть различными. Однако решение, полученное каким-либо способом, единственно, т.е. электромагнитное поле определяется однозначно по заданному распределению источников. Рассмотрим внутреннюю и внешнюю задачи. Для области пространства, ограниченной поверхностью S верна следующая теорема. Монохроматическое электромагнитное поле в определенной ограниченной области V определится однозначно, если: - в каждой точке области среда обладает электрическими либо магнитными потерями ( - заданы источники в этой области; - заданы значения тангенциальной составляющей электрического или магнитного вектора на границе этой области. Очевидно, что при отсутствии потерь в среде возможно существование свободных незатухающих колебаний, не связанных с источниками. В этом случае решение внутренней задачи становится неоднозначным. Внешняя задача. Пусть рассматриваемое пространство неограниченно, т.е. внешней границы S не существует. Это эквивалентно сфере с бесконечно большим радиусом. В этом случае монохроматическое поле определяется в безграничной области однозначно, если: - в каждой точке пространства среда обладает либо электрическими, либо магнитными потерями; - заданы источники в этой области; - заданы значения тангенциальной составляющей электрического или магнитного вектора на внутренней границе области; - все источники находятся на конечном расстоянии от начала координат; - поля убывают на бесконечности быстрее, чем Первые три условия совпадают с соответствующими условиями для внутренней задачи. Таким образом, найденные любым способом решение корректно поставленной задачи отвечает действительному распределению поля, и никакого другого решения быть не может.
|
||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 194; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 .
.
 .
. ,
, 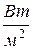 , равна векторному произведению напряженности электрического и магнитного полей:
, равна векторному произведению напряженности электрического и магнитного полей:
 , определяется объемным интегралом:
, определяется объемным интегралом: .
. ;
; .
. .
. ,
, – объемная плотность мощности сторонних сил.
– объемная плотность мощности сторонних сил. .
. , так как
, так как  .
.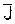 и
и  меньше
меньше  . Ток проводимости
. Ток проводимости  , тогда
, тогда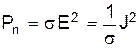 .
. .
. .
. , а первое – на
, а первое – на 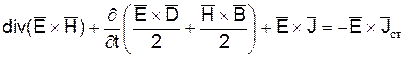 .
. Дано:
Дано:  – плотность потока энергии; v – объемная плотность энергии волны.
– плотность потока энергии; v – объемная плотность энергии волны. – энергетическую скорость электромагнитной волны.
– энергетическую скорость электромагнитной волны. энергия
энергия 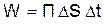 заполняет объем
заполняет объем  , где
, где 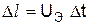 .
. 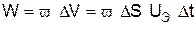 . Приравнивая оба выражения для
. Приравнивая оба выражения для  получим:
получим: ,
, .
.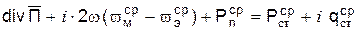 ,
, – мнимая часть сторонней мощности (символ «
– мнимая часть сторонней мощности (символ « » означает усреднение за период).
» означает усреднение за период). .
. ); величина этих потерь может быть весьма мала;
); величина этих потерь может быть весьма мала; .
.


