Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы для расчета моментов инерцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Момент инерции сечения сложной фигуры относительно какой-то оси равен сумме моментов инерции простых элементов этой фигуры относительно той же оси. Jx= JxI+ JxII+ JхIII.
Сумма осевых моментов инерции сечения относительно перпендикулярных осей есть величина постоянная и равна полярному моменту инерции относительно точки пересечения этих осей:
Момент инерции сечения фигуры относительно оси параллельной центральной оси равен центральному моменту инерции плюс произведение площади на квадрат расстояния между осями. Из рисунка 2.5: у = yc + а; х = b + xc;
Jy= Jуc+ b2A; Jxy= Jхcyc+ а bA. Моменты инерции сечения относительно осей xaи ya, повернутых на угол a относительно исходных осей x и y: Jхa= Jхcos2a + Jysin2a - Jxysin2a Jуa= Jхsin2a + Jycos2a + Jxysin2a Jхaуa= [(Jx- Jy)/2] sin2a + Jxy× cos2a. Очевидно, что Jxa+ Jya= Jx+ Jy= const. Таким образом, моменты инерции сечения являются непрерывными функциями угла a. Возможно, такое положение осей координат, при котором Jxaya= 0: [(Jx- Jy)/2] sin2a + Jxycos2a = 0, откуда tg2a = - 2Jxy/(Jx- Jy). Оси, относительно которых центробежный момент инерции сечения равен нулю, называют главными осями инерции. Осевые моменты инерции относительно главных осей имеют наибольшее и наименьшее значение из всех возможных
Моменты сопротивления Осевым моментом сопротивления сечения называется отношение момента инерции относительно данной оси к расстоянию до наиболее удаленной точки от этой оси: Wx= Jx/ymax; Wy= Jy/xmax. Полярный момент сопротивления сечения - это отношение полярного момента инерции сечения к расстоянию от центра до наиболее удаленной точки: Wr= Jr/rmax. Моменты сопротивления характеризуют сопротивление сечения кручению и изгибу. Поэтому их необходимо знать при инженерных расчетах на прочность. Моменты сопротивления измеряют в единицах длины в третьей степени, мм3, м3.
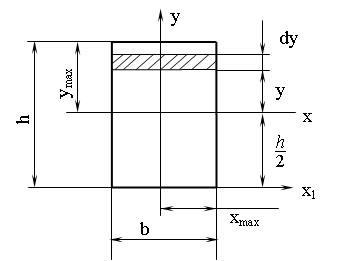
2.2.4 Моменты инерции и моменты сопротивления сечения простых фигур Определим моменты инерции прямоугольника высотой h и шириной b (рисунок 2.6). Момент инерции Выделим в прямоугольнике элементарную полоску высотой dу и шириной b. Элементарная площадь dA = b dy. При этом координата у изменяется от - h/2 до + h/2, тогда
Откуда Jx= b h3/12; аналогично Jy= h b3/12. Момент инерции относительно оси x1, проходящей через основание Jx1= b h3/3. Моменты сопротивления Wx= Jx/уmax= Jx/(h/2) = b h2/6; Wy= h b2/6. Круглое сечение диаметром - d (рисунок 2.7, а). Для круглого сечения Jx= Jy; Jx+ Jy= Jr; 2 Jx= Jr; или Jx= Jy= Jr/2. Полярный момент инерции Выделим элементарное кольцо толщиной dρ на текущем радиусе - ρ. Площадь элементарного кольца dA = 2p×ρ×dρ. D/2 Тогда Jr = ò r2 2 p r dr = 2p ò r3 dr, т.е. Jr = pD4/32» 0,1D4. A 0 Осевые моменты инерции Jx= Jy= 1/2 Jr= pD4/64. Полярный момент сопротивления Wr= Jr/rmax= Jr/(D/2) = p D3/16» 0,2 D3. Осевые моменты сопротивления Wx= Wy= Jx/rmax= Jx/(D/2) = p D3/32» 0,1 D3. Кольцевое сечение с наружным D и внутренним d диаметрами (рисунок 2.7, б).
Рисунок 2.7
Полярные и осевые моменты инерции могут быть получены как разность соответственно полярных и осевых моментов инерции большого и малого круга Jr= p D4/32 - p d4/32 = (p D4/32) [1 – (d/D)4]» 0,1D4× [1 – (d/D)4]. Jx= Jy= (p D4/64) × [1 – (d/D)4]. Моменты сопротивления: Полярный Wr= Jr/rmax= (p D3/16) [1 – (d/D)4] = 0,2 D3× [1 – (d/D)4]. Осевые Wx= Wy= Jx/rmax= (p D3/32)×[1 – (d/D)4] = 0,1 D3× [1 – (d/D)4]. Моменты инерции и моменты сопротивления прокатных профилей (рисунок 2.8) приводятся в таблицах справочников сортамента.
Рисунок 2.8
2.3 Механические свойства материалов
2.3.1 Испытание на растяжение В расчетах на прочность элементов конструкций необходимо знать механические свойства материалов. Для определения механических характеристик материалов проводят испытания цилиндрических или плоских образцов на растяжение. При приложении к испытуемому образцу материала равных по величине противоположно направленных сил образец претерпевает деформацию растяжения. Первоначальная длина l0 увеличивается до l1, поперечные размеры уменьшаются, например первоночальный диаметр уменьшается до d1 (рисунок 2.9). Разность l1 – l0 = Dl называется абсолютным удлинением (при сжатии - абсолютное укорочение). Отношение Dl / l0 = (l1 – l0) / l = e1 называется относительной продольной деформацией. По аналогии d0 – d1 = Dd - абсолютное поперечное сужение.
Рисунок 2.9
D d /do= (do- d1)/do= e2 - относительная поперечная деформация. e1= - μ·e2. μ - коэффициент Пуассона, 0 ≤ μ ≤ 0,5. Для стали μ=0,25-0,3. Испытания на растяжение проводят на машинах, снабженных силоизмерителем и аппаратом для автоматической записи диаграммы растяжения (сжатия) в координатах «сила - удлинение». График зависимости F = j (Dl) называют диаграммой растяжения. Вид диаграммы зависит от размеров образца и физических свойств материала (рисунок 2.10, а). Для исключения этой зависимости диаграмму перестраивают в координаты s (напряжение) - e (относительная деформация), где s = F /А0 и e = Dl / l0. В таком виде диаграмма будет характеризовать только свойства материала образца (рисунок 2.10, б). Диаграмму можно условно разделить на четыре зоны. Первая зона называется зоной упругости ОА, здесь свойства материала подчиняются закону Гука, т.е. между напряжениями и деформациями существует линейная зависимость: s = Е e. Наибольшее напряжение, до которого материал следует закону Гука, называют пределом пропорциональности sП. Е - модуль упругости материала первого рода, характеризующий способность материала сопротивляться упругой деформации. По физическому смыслу Е - напряжение, которое вызывает 100 % удлинение стержня, т.е. e = 1. Для сталей Е = 2,15×105 МПа; для титановых сплавов Е = 1,1×105МПа; для алюминиевых сплавов Е = 0,7×105МПа. Вблизи точки А можно отметить точку К, в которой после снятия нагрузки в образце возникает остаточная деформация до 0,005 %. Напряжение sy из точки К называют пределом упругости. Напряжения sП и sy трудно определяются, поэтому их не относят к основным механическим свойствам материалов. Если из точки К опустить перпендикуляр на ось Оe, то он разделит диаграмму на две области: левую - область упругих деформаций и правую - область упругопластических деформаций.
а) б) Рисунок 2.10
Вторая зона КD называется зоной общей пластичности или зоной текучести, для нее характерно существенное увеличение деформации образца без заметного увеличения нагрузки. Если образец разгрузить в т. D, то зависимость s = f(e) выразится прямой DЕ, параллельной прямой ОА. При этом полная деформация уменьшится на величину упругой деформации ee= sy/Е и останется пластическая деформация ep - отрезок OЕ. На основе результатов испытаний образцов на растяжение, используя диаграмму, получают важную характеристику механических свойств материала - предел текучести, sТ - напряжение, при котором в материале появляется заметное удлинение без увеличения нагрузки т. С. Горизонтальный участок СД диаграммы называется площадкой текучести. Для тех материалов, у которых на диаграмме отсутствует площадка текучестипринимают условный предел текучести s 0,2 - напряжение, при котором остаточная деформация составляет 0,2 %. Третья зона DВ - зона упрочнения, здесь деформации образца возрастают более интенсивно с увеличением нагрузки по сравнению с зоной упругости ОК. В т. В напряжение достигает максимума и это максимальное напряжение, которое способен выдержать образец, называют пределом прочности или временным сопротивлением s в =Fmax/Аo. Четвертую зону - ВМ - называют зоной местной текучести или зоной разрушения. Удлинение образца происходит с уменьшением силы и сопровождается у пластичных материалов образованием местного сужения - шейки с последующим разрушением образца. При испытании образцов материала на растяжение определяют также предельные пластические характеристики материала: относительное удлинение при разрыве d = (Dl / l0) 100 % и относительное сужение при разрыве j = (DА/А0) 100 %. Хрупкие материалы характеризуются тем, что разрушение происходит без образования заметных остаточных деформаций. Например, на диаграмме растяжения серого чугуна площадки текучести материала нет и разрушение происходит внезапно. Как правило, хрупкие материалы плохо сопротивляются растяжению, их предел прочности примерно в два раза меньше предела прочности пластичных материалов. Например, для чугуна sвр<200 Н/мм2, а для стали 20 sвр>400 Н/мм2.
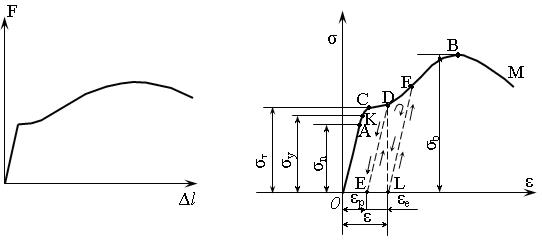
2.3.2 Испытание на сжатие Образцы применяются в виде кубиков или коротких цилиндров: h £ 3d. В начальной части диаграмма сжатия для пластичных материалов совпадает с диаграммой растяжения (рисунок 2.11, а).
Рисунок 2.11
Пределы пропорциональности и текучести у малоуглеродистой стали при растяжении и сжатии можно считать совпадающими (материал изотропный), т.е. sпс = sприsтс = sтр. После точки D образец расплющивается, сила сжатия быстро возрастает и трудно определить sвс, поэтому принимают предел прочности sвс» sвр. Диаграммы напряжений хрупких материалов (чугуна и бетона) даны на рисунке 2.11, б. Основными характеристиками являются предел прочности при сжатии sвс и относительная остаточная деформация при разрушении eост. Для хрупких материалов sвс ³ sвр, т.е. хрупкие материалы сопротивляются сжатию значительно лучше, чем растяжению. В справочниках даются для различных материалов две основные характеристики: sтр(с) и sвр(с), которые называются предельными напряжениями sпред, т.е. такими напряжениями, при которых наступает чрезмерная деформация или разрушение (таблица 2.1). На производстве для оперативного контроля механических свойств материала определяют также его твердость. Под твердостью материала понимают его способность оказывать сопротивление проникновению (внедрению) в него более твердого тела. Наиболее часто определяют твердость по Бринеллю - в поверхность исследуемой детали вдавливается шарик Æ 10 мм из закаленной стали при силе 30 кН. Число твердости НВ равно отношению силы давления к площади поверхности полученного отпечатка. У материалов с большой твердостью,
Таблица 2.1
По величине твердости сталей можно определить приблизительно их временное сопротивление: НВ» 0,34 sв.
2.3.3 Определение допускаемых напряжений На основании результатов испытаний на растяжение (сжатие) в сертификатах или справочниках приводятся две прочностные механические характеристики: предел текучести sтр(с)и предел прочности sвр(с), которые называются предельными напряжениями, при которых наступает чрезмерная деформация или разрушение. Чтобы не доводить детали до разрушения, расчет ведут не по предельным напряжениям, а по несколько меньшим значениям, которые называются допускаемыми напряжениями. Допускаемым напряжением (нагрузкой) называется такое максимальное напряжение (нагрузка), которое можно допустить в опасном сечении детали при условии ее надежной работы в период эксплуатации. Условия прочности: s £ [s]; F£[F]. Левая часть неравенства s, F - фактически действующее в опасном сечении напряжение, нагрузка (расчетная или рабочая). Правая часть - допускаемое напряжение, нагрузка [s], [F]. Запас прочности относительно предельных напряжений (нагрузок) определяется коэффициентом запаса прочности [s]: [s] = sпред /[s]. Для определения допускаемых напряжений необходимо правильно определить предельные напряжения для данного материала и правильно выбрать коэффициент запаса прочности. Механическим характеристикам материалов свойственно сравнительно большое рассеяние при испытаниях серии идентичных образцов, изготовленных из материала даже одной плавки. Например, для стандартных образцов из стали 38ХА sв = 950 - 1200 МПа. Причинами рассеяния являются различия в микроструктуре, размерах образцов, точности измерения нагрузки и т.п. Для совокупности всех плавок металла данной марки рассеяние становится еще большим в связи с дополнительным межплавочным рассеянием механических свойств, вызванных вариациями химического состава, металлургических факторов, прокатки и термообработки. Допускаемые напряжения определяются двумя методами: аналитическим и табличным. Аналитический метод. В качестве предельных напряжений выбирают одну из нормативных механических характеристик материала. Для пластичных материалов при статическом нагружении (опасно появление остаточных деформаций) - предел текучести: sпред.= s т р(с). Для хрупких материалов при статическом нагружении (опасно разрушение) - предел прочности sпред.= sвр(с). Общий коэффициент запаса прочности определяется как произведение частных коэффициентов. Для машиностроения принят метод трех коэффициентов: [s] = s1×s2×s3, где s1 - коэффициент, учитывающий точность расчетов, правильность выбранной схемы, достоверность нагрузок и т.д.: s1= 1...1,4 и > до 2...3; s2 - коэффициент, учитывающий степень ответственности детали s2= 1,0...1,5, большие значения - при большой степени ответственности; s3 - коэффициент, учитывающий надежность материала, механические свойства, технологию обработки и т.д.: s3 = 1,2 - 2,2 - для пластичных материалов; s3 = 2 - 4 - для хрупких материалов. Коэффициенты выбираются из таблиц в зависимости от предельных характеристик. [s т ] = s1×s2×s3 т- коэффициент запаса прочности при предельной характеристике, равной s т р(с) . [sв] = s1×s2×s3в - коэффициент запаса прочности при предельной характеристике sвр(с). Табличный метод. Для ориентировочных или предварительных расчетов, когда не требуется особой точности, пользуются табличным методом определения допускаемых напряжений. Значения, приведенные в таблицах, являются результатом укрупненных вычислений по формуле [s] = sпред./[s] или установлены на основе опыта эксплуатации. Выбор допускаемых напряжений является весьма ответственным этапом расчета, т.к. определяет эксплуатационные и экономические характеристики механизма или конструкции.
2.4 Растяжение и сжатие, смятие и сдвиг
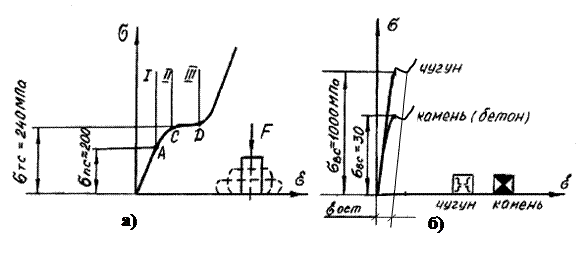
2.4.1 Растяжение (сжатие) Растяжением (сжатием) называется такой вид деформации, при котором в поперечном (перпендикулярном оси) сечении стержня возникает только продольная растягивающая (сжимающая) сила. Модель растягиваемого стержня широко используется в расчетах болтов, ремней передач, стержней ферм, лопаток турбин и др. Для определения величины продольной силы Fz используют метод сечений (рисунок 2.12).
Рисунок 2.12
Продольная сила Fz, приложенная в центре тяжести произвольного сечения стержня, является равнодействующей внутренних сил dFz = s×dА, действующих на бесконечно малые площадки поперечного сечения площадью А: Fz = ò s dА. А Из этого уравнения нельзя найти закон распределения нормальных напряжений по поперечному сечению. Однако, если предположить, что в пределах действия закона Гука плоские поперечные сечения стержня смещаются при растяжении параллельно начальным положениям, оставаясь плоскими, то нормальные напряжения во всех точках сечения должны быть одинаковыми, т.е. s = const, тогда Fz = s×А и s = Fz /А. Таким образом, нормальное напряжение в поперечном сечении стержня при растяжении равно отношению продольной силы к площади сечения. При сжатии стержня напряжения имеют отрицательный знак: нормальная сила направлена в тело стержня. Нормальные напряжения в элементах конструкций не должны превышать допускаемые напряжения: s = Fz / А £ [s]. Данное условие прочности при растяжении позволяет решать задачи расчета элементов конструкций на прочность: 1) при известных размерах поперечного сечения детали А и известном допускаемом напряжении [s] определяют допускаемые нагрузки: F £ А [s]; 2) определяют площадь поперечного сечения по заданной силе и допускаемому напряжению: А ³ Fz /[s], например, для круглого сечения: 3) при известной силе и площади поперечного сечения детали определяют напряжения и проверяют, не превышают ли они допускаемые: s = Fz /А £ [s]. Итак, напряжения при растяжении (сжатии) s = Fz /А. С другой стороны, согласно закону Гука в пределах малых деформаций напряжения прямо пропорциональны вызываемой ими относительной деформации s = Е×e1. Так как относительная деформация e = Dl/lо, тогда Fz /А = E Dl/lо, откуда Dl = Fz lo/(А×Е). То есть, в пределах малых деформаций абсолютное продольное удлинение прямо пропорционально силе Fz и первоначальной длине стержня l oи обратно пропорционально модулю упругости Е и площади поперечного сечения А. Произведение Е×А называется жесткостью сечения стержня при растяжении (сжатии). В некоторых случаях при работе конструкции на сжатие работоспособность ее определяют не величиной допускаемой нагрузки или допускаемого напряжения, а величиной допускаемой деформации. В том случае находят фактическое абсолютное удлинение и сопоставляют его с допускаемым [D l ], такие расчеты называются расчетами на жесткость: Dl = Fz l/(E×А) £ [Dl] - сосредоточенная нагрузка или Dl =q l2/(2E×А) £ [Dl] - распределенная нагрузка. Опыты показывают, что удлинение стержня в осевом направлении при растяжении сопровождается уменьшением его поперечных размеров, т.е. наряду с продольной возникает поперечная деформация стержня: e2= -Db/bo, где Db = bo-b1, b – ширина стержня. Знак минус показывает, что при растяжении поперечные размеры уменьшаются. Отношение поперечной деформации к продольной, взятое по абсолютной величине, называют коэффициентом Пуассона m = |e2/e1 | откуда e2= - me1, учитывая, что e1= s /Е, то e2= -m s /Е. На основе опытных данных: - для сталей m = 0,25 - 0,3; - для алюминиевых сплавов m = 0,3 - 0,35; - для медных сплавов m = 0,35.
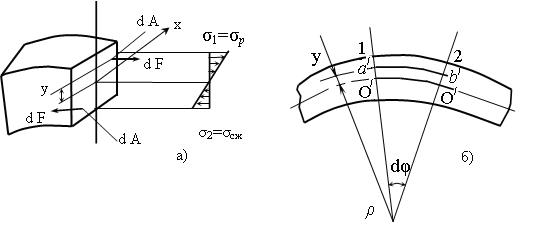
2.4.2 Смятие Если два тела соприкасаются между собой по площади и подвергаются сжимающей нагрузке, то общие поверхности соприкосновения называют поверхностями контакта. На поверхностях контакта возникают напряжения смятия. При расчете на смятие допускают, что силы взаимодействия равномерно распределены по поверхности соприкосновения и в каждой точке нормальны к этой поверхности, т.е. возникают нормальные напряжения. Элементарная сила на элементарной площадке dFсм= sсм×dА. Полная сила:
Тогда, основное условие прочности на смятие: scм= Fcм/Aсм£ [sсм]. Допускаемое напряжение на смятие: [sсм]» 1,5...2,5 [sр](с) (рисунок 2.13, а). Если контакт деталей осуществляется по поверхности полуцилиндра, то площадь смятия определяется как проекция поверхности контакта на диаметральную плоскость Асм= d × l (рисунок 2.13, б).
а) б) Рисунок 2.13
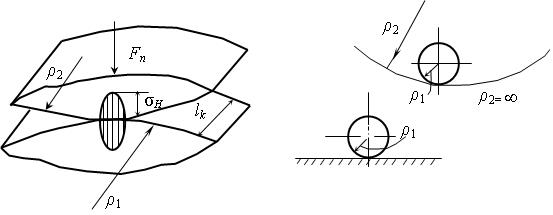
Для многих деталей контакт происходит не по площади, а по линии или точке. В этом случае напряжения смятия определяют по теории контактных напряжений. Под действием нагрузки, прижимающей тела друг к другу в направлении по нормали к их поверхностям, в поверхностных слоях материала деталей возникают местные деформации и контактные напряжения. Давления по площадке контакта распределяются по эллиптическому закону. Максимальные контактные напряжения возникают в центре (точке контакта) (рисунок 2.14, а). Контактные напряжения определяются по формуле Беляева-Герца:
m - коэффициент Пуассона; q = Fп / lк - интенсивность силы давления по длине контактной линии; Епр= 2Е1Е2/(Е1+ Е2) - приведенный модуль упругости материалов, при Е1= Е2= Е; Епр= Е; 1/rпр= 1/r1± 1/r2 - приведенная кривизна поверхностей в месте контакта (рисунок 2.14, а). Знак «-» - одна из поверхностей вогнута. Если одна поверхность прямолинейна, т.е. r2= ¥, то rпр= r1 (рисунок 2.14, б,в).
а) в) Рисунок 2.14
Сдвиг - это деформация, вызываемая противоположно направленными силами, лежащими в близких параллельных плоскостях. Результатом сдвига является срез, например, резание материала ручными или механическими ножницами (рисунок 2.15). При сдвиге происходит перекос прямых углов элементарных параллелепипедов. Степень деформирования определяется величиной, которая называется абсолютной деформацией (абсолютным сдвигом). Деформация сдвига, доведенная до разрушения, называется срезом. Отношение абсолютного сдвига к расстоянию между сдвигающимися сечениями - относительная деформация (относительный сдвиг): D h /a = tg g. В виду малости величин tg g ≈ g = Dh/a. (рисунок 2.15, б). Величина g - относительный сдвиг или угол сдвига. Внутренние силы, уравновешивающие внешние силы, приложенные к отмеченной части, называются поперечными (перерезывающими силами) FQy, т.к. они действуют перпендикулярно оси стержня. Поперечная сила складывается как сумма элементарных внутренних сил:
Если принять допущение, что касательные напряжения распределяются по сечению равномерно и равны, т.е. t = dFQy/ dA = const. FQy= t A = F, откуда t = FQy/A £ [tc] - основное условие прочности при сдвиге. Для пластичных материалов [tc] = (0,5 - 0,6) [sp]. Из диаграммы касательных напряжений в пределах пропорциональности t = G×g, где G - модуль упругости 2 рода (модуль сдвига) (рисунок 2.16). Между G, Е и m существует зависимость: G = Е /[2 (1 + m)]; G = 0,8×105H/мм2- для стали. С учетом вышеприведенных соотношений Dh = F×a/G×А - закон Гука для абсолютной деформации при сдвиге. G×А - жесткость при сдвиге, определяется материалом и размерами поперечного сечения.
Рисунок 2.15
Рисунок 2.16
2.5 Кручение и изгиб
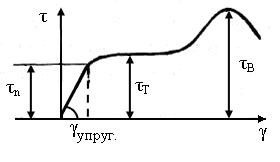
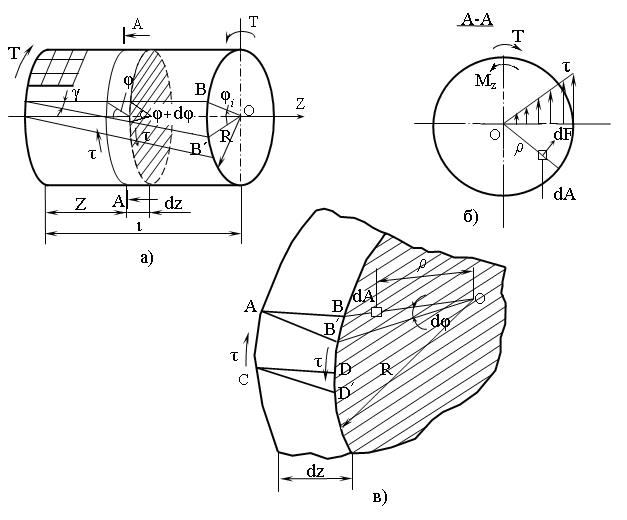
2.5.1 Напряжения при кручении Кручение - это деформация, вызываемая действием пар сил, лежащих в параллельных плоскостях, перпендикулярных оси стержня. На основании опытных данных известно: 1) если на поверхность вала нанести сетку в виде квадратов, то при приложении вращающего момента Т квадраты перекашиваются, обращаясь в ромбы, т.е. подвергаются деформации сдвига (рисунок 2.17, а); 2) образующие поворачиваются на один и тот же угол g; 3) расстояния между поперечными сечениями dz практически не изменяются, следовательно, в направлении параллельном оси стержня Z нормальное напряжение отсутствует s = 0; 4) сечения круглые и плоские до деформации остаются плоскими, но поворачиваются вокруг оси на некоторый угол, называемый углом закручивания j; величина этого угла пропорциональна величине вращающего момента и расстоянию между сечениями; 5) радиусы поперечных сечений при деформации остаются прямыми. На основании этих допущений в расчетах предполагают, что сечения плоские до закручивания остаются плоскими после закручивания; расстояния между поперечными сечениями не изменяются, а радиусы поперечных сечений при деформации остаются прямыми. В соответствии с этими гипотезами материал в поперечных сечениях подвергается чистому сдвигу, т.е. при кручении стержня круглого поперечного сечения по площадкам, перпендикулярным к оси вала, возникают только касательные напряжения (рисунок 2.17, б).
Рисунок 2.17
Разрежем мысленно скручиваемый вал на расстоянии z и отбросим правую часть. Левая оставшаяся часть должна находиться в равновесии под действием вращающего момента Т и крутящего момента Мz от внутренних сил dF, которые заменяют действие отброшенной части (рисунок 2.17, б). Мz = Т. Выделим элементарную площадку dA. Сила, приложенная к ней, будет: dF = t × dA, где t - касательное напряжение в данной точке. Элементарный момент от этой силы dMz= dF×r = t×dA×r. Крутящий момент равен сумме элементарных моментов, т.е. интегралу по площади:
Из полученного уравнения величину касательных напряжений найти не можем, т.к. не знаем, как они распределяются по сечению, то есть, задача статически неопределимая. Для раскрытия статической неопределимости обратимся к рассмотрению упругих деформаций вала. Рассмотрим два сечения на элементарном расстоянии dz (рисунок 2.17, в). Деформации: абсолютного сдвига Dh = B B' = R dj. относительный сдвиг g = В В'/A B = R×dj /dz. По закону Гука при сдвиге касательные напряжения в точке В: tВ= G g = G×R(dj/dz); G = E/[2( 1 +m)] - модуль упругости второго рода, для стали G = 0,8 × 105МПа. Касательные напряжения в любой площадке на расстоянии r: t = G (dj/dz)×r (2.2) Подставим уравнение (2.2) в (2.1): Мz= ò G (dj/dz)×r×dА×r. А При интегрировании по площади ни j, ни z не изменяются, то есть G (dj/dz) = соnst; Мz= G (dj/dz) ò r2dА = G× Jr×(dj/dz); А так как ò r2dА = Jr; или dj/dz = Mz/G×Jr. (2.3) А Подставим уравнение (2.3) в (2.2): t = (Мz/Jr)×r. Наибольшие напряжения будут при r = rmax= R и Mz= Mzmax; tmax= (Mz/Jr) × rmax= Mzmax/Wr, где Wr= Jr/rmax = p d3/16» 0,2 d3 - полярный момент сопротивления круглого вала или момент сопротивления сечения при кручении. Основное условие прочности при кручении: tmax= Mz max/Wr£ [t]. (2.4) Допускаемое напряжение при кручении: [t] = (0,5...0,6)×[s]. 3 _________ Тогда диаметр вала из условия прочности d³ Ö Mz/ 0,2 [t].
2.5.2 Деформации при кручении Деформации при кручении характеризуются углом поворота одного сечения относительно другого или углом закручивания dj/dz = Mz/G×Jr, откуда dj = (Mzdz)/(G×Jr).
На длине равной l угол закручивания будет: l j= ò (Mzdz)/(G×Jr) = (Mz×l)/(G×Jr) - закон Гука при кручении, (2.5) 0 где G×Jr - жесткость сечения стержня при кручении. Принимая l = l/(G×Jr) - крутильная податливость стержня, получим, что j = l×Mz. Если площадь сечения изменяется по длине стержня ступенчато, а Мкр скачкообразно, то полный угол закручивания определяют, суммируя углы закручивания по участкам, в пределах которых Мкр и Jr постоянны. Тогда условие жесткости скручиваемого вала: n j = S (Mzili)/(G×Jri) £ [j] (рад), i=1 n или jo= [S (Mzili)/(G×Jri)] (180o/p) £ [j] (o), i=1 или q = (180o/p) [Мкр/(G×Jr)] град/м. Угол закручивания на единицу длины бруса называют относительным углом закручивания q = j / l = Мz/G×Jr, рад/м. q = (180 o/ π) · Мz/G×Jr, град/м. Допускаемое значение относительного угла закручивания зависит от конструкции [q]» 0,25 до 1,0 град/м. Диаметр вала с учетом обеспечения жесткости:
Таким образом, размеры вала следует определять не только из условия прочности (2.4), но и из условия жесткости (2.5).
2.5.3 Напряжения при изгибе Чистым называют такой изгиб, при котором в сечениях изгибаемой балки возникают только нормальные напряжения. На основании опытных данных известно (рисунок 2.18): 1) при изгибе одни волокна растягиваются (аb), другие сжимаются (сd), следовательно, имеется слой волокон, который отделяет сжатую зону от растянутой (рисунок 2.18, б); 2) изменяются и поперечные размеры балки: ширина балки внизу увеличивается, вверху ширина балки уменьшается, т.к. e2= -m· e1; 3) поперечные сечения 1-1, 2-2 остаются прямыми, но наклоняются друг к другу на некоторый угол dj; 4) линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной осью (ось x); 5) нейтральная ось и ось, проходящая через центр сечения перпендикулярно нейтральной оси, являются главными центральными осями. Ограничения при расчете: Рассматривают участок, где балка подвергается чистому изгибу, т.е. Fy= 0, Мx= сonst (между опорами). Балка имеет хотя бы одну плоскость симметрии, и все внешние силы лежат в этой плоскости, такой изгиб называется плоским, т.к. изогнутая ось лежит в плоскости действия силы.
Рисунок 2.18
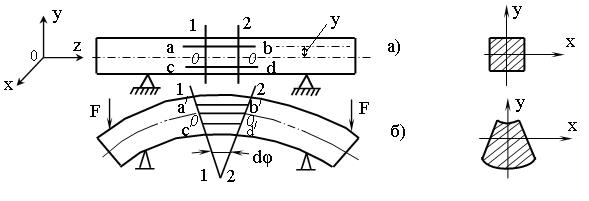
Материал балки подчиняется закону Гука, и модуль упругости при растяжении и сжатии одинаков. Опытные наблюдения дают основания для принятия следующих гипотез: - сечения после изгиба остаются плоскими, но поворачиваются вокруг нейтральной оси на угол dj; - волокна не оказывают давления друг на друга (syи sz= 0), следовательно, подвергаются простому растяжению или сжатию. Рассмотрим сечение балки. Выделим элементарные площадки dA сверху и снизу от нейтральной оси x на расстоянии у (рисунок 2.19, а). Элементарная сила (сверху растягивающая, снизу - сжимающая) будет равна dF = s dA, где s - нормальное напряжение при растяжении. Элементарный изгибающий момент от этой силы: dMx= dF y = sу dA. Изгибающий момент равен сумме элементарных моментов, т.е. интегралу по площади:
Из полученного уравнения величину Мхнайти не можем, т.к. не знаем, как распределяются напряжения по сечению, т. е. задача статически неопределима. Обратимся к рассмотрению деформаций (рисунок 2.19, б). r - радиус кривизны нейтрального слоя. Длина волокна до изгиба аb = OO = l. Длина нейтрального слоя после изгиба остается постоянной ОО = О´О´ = r×dj. Длина волокна ab после изгиба увеличилась l1= a´b´ = (r+у)×dj. Абсолютное удлинение Dl = l1- l = у dj. Относительное удлинение e = Dl/l =(у×dj)/(r×dj)= у/r. По закону Гука: s = Е e = Е (у/r). (2.7) Подставим (2.7) в (2.6): Мx= (Е /r)ò у2dA = E Jx/r, где ò у2dA = Jx - осевой момент инерции, А 1/r = Mx/(E Jx) - кривизна балки (2.8)
Рисунок 2.19
Подставим уравнение (2.8) в (2.7): s = (Мx/Jx) у. Из этой формулы следует ряд важных выводов: - центр тяжести стержня является началом координат для анализа напряжений и приведения внешних сил; - напряжения изгиба зависят от значений Мx, Jx и координаты рассматриваемой точки; - напряжения в любой точке, лежащей на одинаковом расстоянии от нейтральной линии, равны между собой; - нормальные напряжения не зависят от модуля упругости стержня, например, два конструктивно одинаковых стержня из стали (Е = 2×105МПа) и титанового сплава (Е = 1,1×105МПа) при равной внешней нагрузке имеют одинаковые напряжения в соответствующих точках сечений. На нейтральной оси при у = 0, s = 0. Наибольшие напряжения будут при у = уmax; smax= (Mx max/Jx) уmax= Mxmax/Wx, где Wx= Jx/уmax - осевой момент сопротивления относительно нейтральной оси или момент сопротивления сечения изгибу. Условие прочности при изгибе: smax= Mxmax/Wx |
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 1277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.017 с.) |

 , где
, где 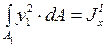 и т.д.
и т.д.
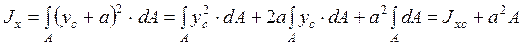 ;
;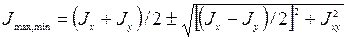 .
.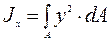 .
.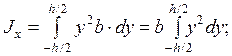
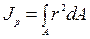



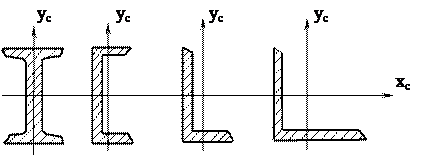

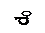


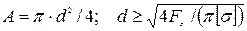 ;
;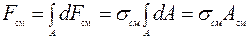 .
.
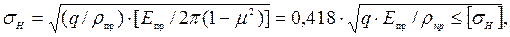

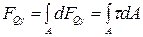 (рисунок 2.15, в).
(рисунок 2.15, в).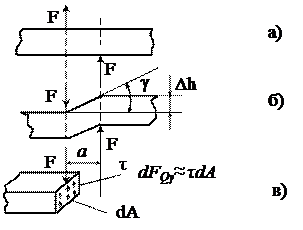

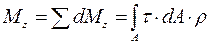 (2.1)
(2.1)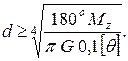
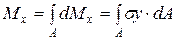 (2.6)
(2.6)