
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные параметры эвольвентных зубчатых колесСодержание книги
Поиск на нашем сайте
Боковые профили зубьев ограничены эвольвентами, которые построены на основных окружностях (рисунок 3.12). По высоте зубья ограничены окружностью впадин и окружностью головок. Все понятия и параметры зубчатых колес стандартизованы. Различают индексы, относящиеся: - b – к основной окружности - f – к окружности впадин - а – к окружности головок Расстояние pi между одноименными профилями двух соседних зубьев, измеренное по дуге любой окружности, называют окружным шагом зубьев. Окружной шаг состоит из окружной толщины зуба - si и окружной ширины впадины - li
Центральный угол Угловой шаг зависит от числа зубьев. У зубчатых колес, работающих в паре, Для непрерывной передачи окружной шаг должен быть одинаков у обоих колес
откуда где На каждом колесе есть базовая окружность для определения элементов зубьев и их размеров, которую называют делительной. На делительной окружности ширина зуба – s равна ширине впадины - l.
где m – делительный модуль или просто модуль – стандартный основной параметр, используемый для расчета размеров зубчатого колеса с данным числом зубьев, мм. Делительная окружность в торцевом сечении делит зуб на две части: головку и ножку (рисунок 3.12).
Рисунок 3.12
Делительной головкой зуба (головкой) называется часть зуба, расположенная между делительной окружностью и окружностью головок. Высота головки зуба - ha. Делительной ножкой зуба (ножкой) называется часть зуба, расположенная между делительной окружностью и окружностью впадин, высота ее - hf. Общая высота зуба h=ha+hf. Высота ножки зуба больше высоты головки, чтобы вершины зубьев одного колеса не упирались во впадины другого. У парных зубчатых колес зубья одинаковые. Наименьшее расстояние – с между окружностью вершин одного колеса и окружностью впадин другого, носит название радиального зазора c=hf -ha. При проектных расчетах удобно пользоваться относительными величинами по делительной окружности, для которой модуль имеет стандартную величину и которая является базовой для определения размеров зубьев. Высота головки зуба, мм
где Радиальный зазор, мм
где с * = 0,25 – коэффициент радиального зазора. Высота ножки зуба, мм
Полная высота зуба, мм
Диаметр делительной окружности, мм
Диаметр основной окружности, мм
Диаметр окружности выступов, мм
Диаметр окружности впадин, мм
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.15 (0.006 с.) |

 ;
; ;
; .
. .
.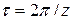 называется угловым шагом.
называется угловым шагом. при
при 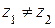 .
. . Окружной шаг можно измерить по любой окружности и для любой окружности должно быть целое число шагов и зубьев
. Окружной шаг можно измерить по любой окружности и для любой окружности должно быть целое число шагов и зубьев
 ,
, - линейная величина в
- линейная величина в  раз меньше окружного шага зубьев
раз меньше окружного шага зубьев 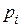 называется окружным модулем.
называется окружным модулем.
 ,
,


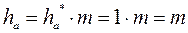 ,
, - коэффициент высоты головки.
- коэффициент высоты головки.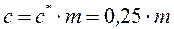 ,
, .
. .
.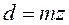 .
.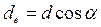 .
.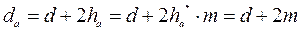 .
. .
.


