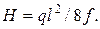Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Допускаемое напряжение на устойчивостьСодержание книги
Поиск на нашем сайте
где ny - коэффициент запаса устойчивости. Коэффициент запаса устойчивости: Установим связь между допускаемыми напряжениями
Обозначим
где φ - коэффициент продольного изгиба или коэффициент уменьшения допускаемых напряжений. Величина φ зависит от материала и гибкости Условие устойчивости С учетом (2.29) можно записать окончательно:
Для стержней из сталей Ст 2, Ст 3, Ст 5, 10ХСНД, 10Г2С1 и др. средние значения λ и φ следующие: λ... 10 20 40 60 80 100 120 140 160 φ... 1 0,95 0,9 0,8 0,65 0,5 0,35 0,3 0,25 Проверка сжатых стержней на устойчивость не исключает проверки на прочность для чистого сжатия. При проектном расчете из условия устойчивости (2.30) определяют площадь сечения:
Для подбора сечений стержней, работающих на продольный изгиб, применяют метод последовательных приближений. Задаемся величиной коэффициента φ (обычно 0,5 - 0,6). Из формулы (2.31) определяем площадь по первому вычислению. По минимальному моменту инерции находим радиус инерции и гибкость
По таблицам для этой гибкости уточняем величину коэффициента продольного изгиба φ. Подставляем значение φ в условие устойчивости. Находим расчетные напряжения на устойчивость:
Если расчетное значение напряжения отличается от допускаемого больше, чем на (+10%), (-5%), то сечение соответственно надо, либо увеличить, либо уменьшить и вновь повторить проверку. Рациональные формы сечения при расчете на устойчивость Рациональной является такая форма сечения, которая обеспечивает устойчивость сжатого стержня при наименьшем расходе материала. Вопрос о выборе формы поперечного сечения является не менее важным, чем вопрос о величине площади сечения. Следует добиваться равенства осевых моментов инерции сечения. Как показывает практика, наиболее выгодными следует признать кольцевые, а так же коробчатые тонкостенные сечения (рисунок 2.44). Если сечение состоит из двух профилей, причем
из условия
Рисунок 2.44 Расчет гибких нитей Совершенно гибкой называется нить, которая способна сопротивляться только растяжению. Из шести компонентов внутренних сил в поперечных сечениях такой нити только осевая растягивающая сила не равна нулю. В инженерной практике широко распространены системы, которые с известным приближением могут рассматриваться как гибкие нити. Таковыми являются воздушные линии электрических проводов, провода телеграфной сети, контактные провода электрофицированных железных дорог и трамваев, цепи висячих мостов, тросы канатных дорог и т.п.
Точки подвеса нити могут находиться на одном или на разных уровнях. При расчете на прочность длинных гибких нитей, кроме других нагрузок, существенное значение имеет их собственный вес. Пусть весомая гибкая нить постоянного поперечного сечения подвешена в двух точках, расположенных на одном уровне (рисунок 2.45, а) или на разных уровнях (рисунок 2.45, б).
Рисунок 2.45
Под действием собственного веса нить провисает по некоторой кривой l1 - расстояние между точками А и В подвеса нити; l - пролет, равный горизонтальной проекции расстояния l1; h - разность уровней точек подвеса нити; f - удаление нити от прямой АВ, соединяющей точки подвеса нити, измеренное посредине пролета; L - длина неподвешенной нити; q - интенсивность нагрузки на единицу длины нити. В случае одинакового уровня точек подвеса величина f является удалением низшей точки нити от горизонтальной линии АВ и называется стрелой провисания. Нагрузка q может быть не только собственным весом, но и включать в себя другие нагрузки, например, вес льда при обледенении проводов, давление ветра. Эти нагрузки предполагаются также равномерно распределенными по длине нити. В случае, когда нагрузка состоит из собственного веса нити, то где qn - вес единицы длины провода; γ - вес единицы объема материала: А - площадь поперечного сечения нити. При обледенении проводов q = qn + qл, где qл - вес льда на единице длины провода. Толщину корки льда в зависимости от климатического района принимают равной 0,5 - 2,5 см. Перечисленные нагрузки действуют в вертикальной плоскости, давление же ветра на провод - в горизонтальной плоскости. Интенсивность его qв определяют, умножая давление ветра р на площадь диаметрального сечения единицы длины провода:
где к = 1,2 - аэродинамический коэффициент; α = 0,85 - коэффициент неравномерности ветра;
d - диаметр провода с учетом его увеличения за счет обледенения. Выражая
Здесь скорость ветра v - в метрах в секунду, а диаметр провода d - в метрах. Суммарную интенсивность нагрузки на провод найдем в результате геометрического сложения вертикальной и горизонтальной нагрузки:
При этом, естественно, плоскость действия суммарной нагрузки, совпадающая с плоскостью провисания нити, не будет вертикальной. На практике провисание нити чаще всего бывает небольшим - таким, при котором длина нити по кривой провисания мало отличается от длины пролета (обычно не более, чем на 10%). Ограничимся рассмотрением только таких пологих нитей. В этом случае для упрощения расчетов с достаточной степенью точности можно считать, что нагрузка, действующая на подвешенную нить, равномерно распределена не по длине нити, а по длине линии АВ, соединяющей точки подвеса (рисунок 2.46,а). Для удобства вычислений эту нагрузку q заменяем статически эквивалентной нагрузкой Очевидно, Рассмотрим равновесие нити. Так как нить предполагается совершенно гибкой, то растягивающая сила в каждом поперечном сечении должна быть направлена по касательной к кривой провисания нити. В точках прикрепления эти силы равны реакциям опор. Обозначим последние соответственно через ТА и Тв. Выберем, начало координат в левой точке подвеса нити, и направим оси координат так, как показано на рисунке 2.46.
Рисунок 2.46
Заменяя реакции опор их горизонтальными и вертикальными составляющими, запишем уравнения равновесия нити:
Из этих уравнений следует, что: НА = НB = Н;
Так как из трех уравнений равновесия нельзя определить четыре неизвестных (НА, RA, НВ и RB), то задача является один раз статически неопределимой. Рассмотрим равновесие части нити, отсеченной любым сечением (рисунок 2.46, б):
Как видно из выражения, горизонтальная составляющая растягивающей силы в любом поперечном сечении нити постоянна и равна величине Н. Сила Н называется горизонтальным натяжением нити, она может быть определена через провисание f: Таким образом, растягивающая сила в произвольном сечении Как видно, наибольшая растягивающая сила
Для пологих нитей различие между наибольшей растягивающей силой, действующей у более высокой точки подвеса, и натяжением Н невелико. Поэтому с достаточной для практики точностью можно считать, что растягивающая сила в нити постоянна и равна величине натяжения Н. По этой величине обычно и ведут расчет нити на прочность. Удлинение
Стрелу провисания нити f определяют из статического уравнения
Установим физические зависимости, выражающие изменение длины нити от растягивающей силы и от изменения температуры. Как указывалось, для пологих нитей растягивающую силу можно принять равной натяжению Н. При определении удлинений длину нити заменим длиной
Температурное удлинение нити определяется по формуле
где То° - температура в момент подвешивания нити; Т ° - температура, для которой производится расчет нити. Суммарное изменение исходной длины нити
Две последние формулы выражают одну и ту же величину - удлинение подвешенной нити. Приравняв правые части этих равенств, найдем, что
Это уравнение называют уравнением совместности деформаций, оно совместно со статическим уравнением Определив натяжение нити Н, по формуле 2.32 можно вычислить растягивающую силу в произвольном сечении нити, а значит, и
с учетом формулы При расчете нитей удобно ввести понятие удельной нагрузки γ, которая представляет собой интенсивность погонной нагрузки q, отнесенную к площади поперечного сечения нити: С учетом сказанного условие прочности можно записать так:
Заметим, что при расчете электрических проводов сечение нити определяется из электротехнических соображений, а затем выполняется проверочный расчет. Приведем расчетные формулы для часто встречающегося случая нити с точками подвеса, расположенными на одном уровне (рисунок 2.47), т.е. при В этом случае h = 0, реакции в точках подвеса одинаковы: RA = RB = ql/2, наибольшее провисание f будет посредине пролета. Как и ранее, оно связано с натяжением формулами:
Уравнение совместности деформаций принимает вид:
Рисунок 2.47
|
||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.110 (0.012 с.) |

 (2.28)
(2.28) - критическое напряжение;
- критическое напряжение; - для стальных и
- для стальных и 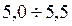 - для чугунных стержней.
- для чугунных стержней. и
и  :
:

 или
или  (2.29)
(2.29) стержня и приводится в таблицах.
стержня и приводится в таблицах.

 (2.30)
(2.30) (2.31)
(2.31)

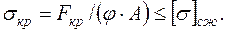
 то можно подобрать таким образом расстояние а, чтобы обеспечить условие:
то можно подобрать таким образом расстояние а, чтобы обеспечить условие:





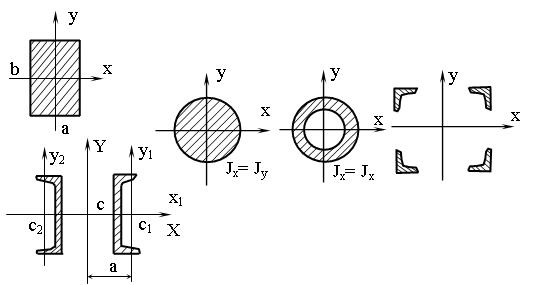

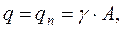



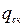 - скоростной напор;
- скоростной напор; кгс/м через скорость ветра v, получаем
кгс/м через скорость ветра v, получаем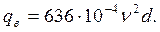

 , распределенной вдоль пролета l.
, распределенной вдоль пролета l. , отсюда
, отсюда 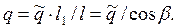



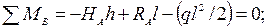


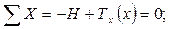
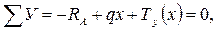 подставим RA, тогда
подставим RA, тогда
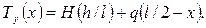
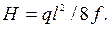
 . (2.32)
. (2.32) действует ввысшей точке подвеса нити (при х = 0):
действует ввысшей точке подвеса нити (при х = 0):
 нити длиной L после подвески определяют по формуле:
нити длиной L после подвески определяют по формуле:

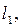 что достаточно точно при малом провисании. Тогда упругое удлинение от растяжения
что достаточно точно при малом провисании. Тогда упругое удлинение от растяжения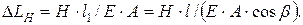



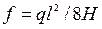 , позволяет определить натяжение нити Н и стрелу провисания f.
, позволяет определить натяжение нити Н и стрелу провисания f. . Зная последнее, проверяем прочность нити:
. Зная последнее, проверяем прочность нити:
 получаем
получаем 
 . Если действует только собственный вес, удельная нагрузка совпадает с объемным весом материала нити.
. Если действует только собственный вес, удельная нагрузка совпадает с объемным весом материала нити.