
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоское (двухосное) напряженное состояниеСодержание книги
Поиск на нашем сайте
Рассмотрим элемент, по граням которого действуют растягивающие напряжения Проведем наклонную площадку (α - сечение) и определим напряжения По принципу независимости действия сил (суперпозиции):
От действия
От действия
Тогда
Наибольшее и наименьшее из всех возможных напряжений в данной точке - это главные напряжения, действующие по площадкам, свободным от касательных напряжений, т.е. при
1) 2) Итак, главные напряжения - это нормальные напряжения, действующие по главным взаимно-перпендикулярным площадкам, причем одно из главных напряжений всегда является наибольшим, а другое наименьшим. Это справедливо и при объемном напряженном состоянии. Максимальные касательные напряжения будут при т.е. равны полуразности главных напряжений и действуют в площадках, наклоненных под углом 45° к главным площадкам.
Рисунок 2.24 Рисунок 2.25
Определим напряжения, действующие по β - площадке, перпендикулярной к α - площадке. По аналогии с одноосным растяжением, формулы (2.12) и (2.13), окончательно получим (рисунок 2.26):
Рисунок 2.26
Сложим (2.16) и (2.18):
согласно (2.14)
Сумма нормальных напряжений по двум любым взаимно-перпендикулярным площадкам есть величина постоянная, равная сумме главных напряжений. Сравнивая (2.17) и (2.19) имеем: Закон парности касательных напряжений справедлив и при плоском (двухосном) напряженном состоянии. Рассмотрим два частных случая: если то и
т.е. на всех элементарных площадках, проходящих через рассматриваемую точку, нормальное напряжение равно σ, а касательное τ=0. Такое напряженное состояние называется равномерным двухосным растяжением (или сжатием). Если тогда а т.е. нормальное напряжение
а) б) Рисунок 2.27
Если главные напряжения равны по величине, но противоположны по знаку (по направлению), то по площадкам, наклоненным к ним на угол Совокупность формул (2.16)...(2.19) дает возможность решать прямую задачу плоского напряженного состояния, т.е. по известным главным напряжениям находить нормальные и касательные напряжения в наклонных площадках. При этом угол α всегда отсчитывают от направления алгебраически большего главного напряжения (против часовой стрелки), а значения главных напряжений подставляют в формулу со своими знаками.
На практике часто имеют дело с обратной задачей, в которой по известным нормальным и касательным напряжениям в наклонных площадках Из формул (2.16)...(2.19):
где α - угол, на который необходимо повернуть нормаль получить направление главного нормального напряжения
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 227; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.183.122 (0.009 с.) |

 и
и  , а третье главное напряжение
, а третье главное напряжение  (рисунок 2.24).
(рисунок 2.24). и
и  , которые вызываются растягивающими напряжениями
, которые вызываются растягивающими напряжениями 




 (2.16)
(2.16) (2.17)
(2.17)



 , тогда
, тогда 
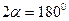
 , тогда
, тогда 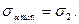
 , т.е.
, т.е.  ,
,  :
: 



 (2.16)
(2.16) (2.17)
(2.17) (2.18)
(2.18) (2.19)
(2.19) (2.20)
(2.20)

 (рисунок 2.27, а)
(рисунок 2.27, а)



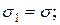


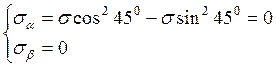 ,
, ,
, а
а 


 возникают только касательные напряжения. Такое напряженное состояние называют чистым сдвигом (рисунок 2.27, б).
возникают только касательные напряжения. Такое напряженное состояние называют чистым сдвигом (рисунок 2.27, б). определяют главные напряжения и положение главных площадок.
определяют главные напряжения и положение главных площадок. (2.21)
(2.21)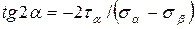 ,
, , чтобы
, чтобы Знак (-) поставлен потому, что угол отсчитывают от нормали рассматриваемой площадки к нормали площадки, где действует
Знак (-) поставлен потому, что угол отсчитывают от нормали рассматриваемой площадки к нормали площадки, где действует 


