
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет статической устойчивости электрической системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Введение Одной из важнейших задач электроэнергетики является обеспечение устойчивости параллельной работы электростанций и энергосистем. Нарушения их устойчивости могут приводить к обесточиванию большого числа потребителей электроэнергии, повреждению оборудования электростанций и сетей и другим тяжелым последствиям. Исследования устойчивости выполняются как на различных этапах проектирования энергосистем, так и при их эксплуатации: при выборе структуры энергосистемы, определении пропускной способности линий электропередачи, выборе средств управления, регулирования, защиты и противоаварийной автоматики. Неотъемлемой частью общей задачи устойчивости является задача устойчивости нагрузки. В энергосистемах возможны случаи, когда нарушение устойчивости генераторов может приводить к нарушениям работы электроприемников, в то же время возможны системные ситуации, которые вызывают торможение и последующее отключение больших групп двигателей при сохранении параллельной работы генераторов, например, при затяжных коротких замыканиях в распределительной сети. В некоторых случаях возможны тяжелые системные аварии, когда нарушается нормальная работа и генераторов и больших масс электроприемников, причем обычно в таких случаях процессы нарушения устойчивости генераторов и электроприемников оказываются взаимосвязанными. Поэтому обеспечение устойчивости двигателей требует к себе такого же внимания, как и обеспечение устойчивости генераторов. При проектировании и эксплуатации систем электроснабжения возникает ряд проблем, для решения которых необходимо провести анализ переходных процессов в узле нагрузки. К таким вопросам относятся определение условий и выбор схемы пуска мощных электродвигателей, определение условий и способов обеспечения успешного самозапуска и ряд других. Настоящее учебно-методическое пособие предназначено для студентов специальностей 140205, 140211, изучающих курс «Переходные процессы в электроэнергетических системах», и для студентов специальности 140610, изучающих курс «Высоковольтное электрооборудование и переходные процессы», и выполняющих в соответствии с учебными планами курсовую работу «Расчет и анализ переходных процессов в электрических системах». Целью курсовой работы является систематизация и углубление теоретических знаний по дисциплине «Переходные процессы в электрических системах», а также освоение упрощенных методов расчета устойчивости.
Задание на курсовую работу Расчет и анализ переходных процессов выполняется применительно к различным схемам электрической системы, в которых электрическая станция связана электропередачей с шинами системы бесконечной мощности. В электрической системе имеется промежуточный отбор мощности для электроснабжения узла нагрузки. Состав узла нагрузки принимается в соответствии с рис.1.1. Трансформаторы Т1 и Т2 связывают узел нагрузки с питающей системой.
Рис.1.1. Расчетная схема исследуемой системы
Программа работы Курсовая работа «Расчет и анализ переходных процессов в электрических системах» состоит из двух частей: первая часть посвящена расчету электромагнитных переходных процессов, а именно расчету токов короткого замыкания в различных точках схемы электроснабжения (К1 – К7). Выполнение этой части расчетов осуществляется согласно рекомендациям, приведенным в [1, 2, 3, 4]. Вторая часть курсовой работы посвящена расчету и анализу электромеханических переходных процессов. В настоящем методическом пособии рассматриваются вопросы именно этой части курсовой работы. Перечень вопросов, предложенный для изучения электромеханических переходных процессов, включает - расчет параметров исходного режима системы, определение напряжений в узлах сети, э.д.с. эквивалентного генератора а) отсутствия АРВ на генераторах электрической станции; б) генератор снабжен АРВ пропорционального действия; в) генератор снабжен АРВ сильного действия. - анализ статической устойчивости эквивалентного асинхронного двигателя. С этой целью определяются параметры эквивалентного асинхронного двигателя и параметры его схемы замещения, строится характеристика мощности, определяется запас устойчивости эквивалентного асинхронного двигателя. - расчет времени пуска асинхронного двигателя. - расчет и анализ процессов самозапуска. - анализ динамической устойчивости системы при коротком замыкании в начале линии, связывающей станцию с системой, определение предельного угла отключения и предельного времени отключения короткого замыкания. Перечень рассматриваемых вопросов может быть изменен по заданию преподавателя.
Электрической системы
Под статической устойчивостью электрической системы понимается ее способность возвращаться к установившемуся режиму после его малых возмущений. Малые возмущения могут возникать в результате изменений режимов работы электрической системы, например, отключения части питающих линий, при оперативных переключениях и т.п. Для расчета и анализа переходных процессов в электрической системе предварительно выполняется расчет исходного установившегося режима ее работы, возмущение этого режима и будет вызывать рассматриваемый переходный процесс. Расчет исходного установившегося режима выполняется с целью определения его параметров: напряжений в узлах сети, э.д.с. генераторных станций и фазовых углов, потоков мощности по участкам сети. Расчеты производятся на основании схемы замещения электрической системы. Расчетная схема замещения электрической системы составляется из схем замещения отдельных элементов системы (генераторов, трансформаторов, линий и т.д.), связанных друг с другом так же, как соединены соответствующие элементы рассматриваемой системы. Расчеты переходных электромеханических процессов удобно выполнять в системе относительных единиц. При этом как параметры элементов схемы замещения системы (сопротивления контуров), так и параметры режима (э.д.с., напряжения, мощности) выражаются в долях от соответствующих величин, принятых за базисные. В качестве таких величин обычно принимают мощность
На других ступенях трансформации базисные напряжения пересчитываются с учетом действительных коэффициентов трансформации трансформаторов к рассматриваемой ступени. Параметры эквивалентных элементов электрической системы определяются по следующим выражениям: - сопротивления генераторов
где
- сопротивления трансформаторов
где
- сопротивления линий
где
Заданные параметры режима (мощность
Рассмотрим определение параметров исходного режима для простейшей схемы выдачи мощности генераторной станции на шины приемной системы бесконечной мощности (рис. 2.1). В системе имеется промежуточный отбор мощности. Мощность нагрузки
Рис. 2.1. Расчетная схема исследуемой системы
Схема замещения рассматриваемой системы при отсутствии АРВ генераторов электрической станции представлена на рисунке 2.2.
Рис. 2.2. Схема замещения расчетной системы
При составлении схемы замещения генераторы без АРВ замещаются э.д.с. Рассмотрим расчет исходного режима при следующих заданных его параметрах: напряжении на шинах системы Предварительно определим расчетную мощность в узле 2:
где Схема замещения преобразуется к виду:
Рис. 2.3. Схема замещения исследуемой системы после преобразования по (2.8)
Расчет потоков мощности по участкам сети выполняется от начала электропередачи к ее концу по следующим выражениям:
На втором этапе при заданном напряжении на шинах приемной системы с учетом потоков мощности, определенных на первом этапе по выражениям (2.9), определяются напряжения в каждой узловой точке сети. При совмещении вектора
где угол ния шин системы Совместив вектор
где угол При совмещении вектора
где Э.д.с. генераторной станции равна:
где Векторная диаграмма напряжений и э.д.с. генератора представлена на рис. 2.4.
Рис. 2.4. Векторная диаграмма напряжений и э.д.с.
Из рисунка 2.4 видно, что напряжения в узлах Полный угол электропередачи
И запаса устойчивости При передаче больших мощностей от крупных электростанций и в ряде других случаев возникает необходимость специального исследования устойчивости энергосистем с целью определения предельных по устойчивости режимов. При выполнении этих расчетов нагрузка в схемах замещения электрических систем упрощенно представляется неизменными сопротивлениями
Емкостные сопротивления
При замещении нагрузки в виде последовательно соединенных активного и индуктивного сопротивлений расчетная схема замещения (рис.2.3) будет иметь вид, изображенный на рис.2.5.
Рис.2.5. Схема замещения сети при представлении нагрузки неизмененными сопротивлениями
Выражение для характеристики мощности генераторной станции имеет вид:
где
Определение собственных и взаимных проводимостей производится методом единичного тока, либо методом преобразования схемы замещения, либо с помощью ЭВМ по специально разработанным программам, например, TKZ-3. Метод единичного тока предполагает расчет режима схемы замещения сети при действии только одного источника питания. С целью определения проводимостей
Рис.2.6. Схема замещения сети, преобразованная для расчета проводимостей
Найденные напряжения источников питания и токи в ветвях позволяют вычислить проводимости
Собственные и взаимные углы потерь определяются как углы, дополняющие до 900 углы
Максимальная мощность, которую можно передать от генераторной станции, определяется как амплитуда угловой характеристики (2.16) и равна:
Предельный угол электропередачи определяется из условия:
откуда Условием обеспечения статической устойчивости системы является условие
Режим работы при передаче максимальной мощности Анализ статической устойчивости по критерию (2.20) сводится к определению максимальной мощности (предела передаваемой мощности)
Согласно [5] коэффициент запаса устойчивости электропередачи по активной мощности должен быть не менее 20 % в нормальном режиме и не менее 8 % в вынужденном (послеаварийном) режиме.
Решение. При отсутствии АРВ генераторов, представлении линии П-образной схемой замещении, неучете активных сопротивлений трансформаторов и их ветвей намагничивания, схема замещения рассматриваемой системы имеет вид, изображенный на рис.2.2. Определим параметры схемы замещения в относительных единицах. Примем в качестве базисных условий: Базисное напряжение на ступени 220 кВ составит:
Базисное сопротивление на ступени 220 кВ равно:
При принятых базисных условиях параметры схемы замещения в соответствии с (
Определим заданные параметры режима в относительных единицах. Напряжение на шинах эквивалентного генератора:
В дальнейшем в расчетах используются параметры, приведенные к базисным условиям, обозначение «*» для краткости опускается. Мощность, выдаваемая с шин генераторной станции:
Мощность нагрузки:
Полученные данные нанесем на схему замещения (рис.2.8).
Рис.2.8. К примеру 2.1. Схема замещения электрической системы
Определим э.д.с. генераторной станции по выражению (2.13):
Внутренний угол генератора равен
Напряжение в узле 1 равно:
Мощность
Зарядная мощность в начале линии W1 определяется величиной напряжения в узле 1:
Мощность
Мощность конца линии 1 – 2:
Напряжение в узле 2 равно:
Зарядные мощности
Найдем расчетную мощность узла 2:
Емкостной характер расчетной мощности обусловлен превышением суммарной зарядной мощности линий 220 кВ, примыкающих к узлу 2, над реактивной мощностью нагрузки. Представим расчетную нагрузку неизменным сопротивлением
Мощность начала линии W2 равна
Мощность конца этой линии равна:
Напряжение на шинах приемной системы равно:
Внешний угол электропередачи равен сумме углов
Полный угол электропередачи равен сумме внутреннего
Определим собственные и взаимные проводимости методом единичного тока. С этой целью рассчитаем распределение токов и напряжений в рассматриваемой схеме, приняв напряжение второго источника питания ( Расчетная схема замещения для расчета проводимостей методом единичного тока представлена на рис.2.9.
Рис. 2.9. К примеру 2.1. Расчетная схема для расчета собственных и взаимных проводимостей
В результате последовательного расчета режима такой схемы находим:
Собственные и взаимные проводимости в соответствии с (2.17), (2.18) равны:
Собственные и взаимные углы потерь равны:
Подставив полученные значения
Для проверки вычислим активную мощность в исходном режиме. С этой целью значение полного угла электропередачи
Результат вычислений совпал с заданным значением активной мощности генераторной станции, следовательно расчеты выполнены верно. Предел передаваемой мощности находится как максимум полученной характеристики мощности:
Полный угол электропередачи, соответствующий этому пределу, определим из соотношения:
Коэффициент запаса статической устойчивости согласно (2.21) равен:
Для построения угловой характеристики вычислим значения мощности при различных углах
Табл.2.1 Результаты расчета мощности генераторной станции при различных углах
Рис. 2.10. Угловая характеристика мощности электропередачи
Вывод: статическая устойчивость рассматриваемой системы при заданных условиях обеспечивается, поскольку полный угол электропередачи в исходном режиме меньше предельного:
Асинхронного двигателя Те или иные свойства нагрузки оказывают непосредственное влияние на устойчивость параллельной работы станций. Однако, характеристики нагрузки существенны не только с этой точки зрения. В определенных условиях нагрузка сама может оказаться неустойчивой. Основными причинами, которые могут вызывать нарушение статической устойчивости электродвигателей, является значительное увеличение внешнего сопротивления, например, в результате отключения части питающих линий, и, чаще всего, снижение напряжения в узле нагрузки. Снижение напряжения в узле нагрузки приводит к торможению двигателей, увеличению потребляемой ими реактивной мощности и дальнейшему снижению напряжения. Это может вызвать нарушение устойчивости других, еще работающих двигателей. В результате может возникнуть лавина напряжения – аварийный режим в электрической системе, характеризуемый глубоким снижением напряжения в ее узлах, вначале медленным, потом более быстрым, ростом реактивной и снижением активной мощности в сети.
Расчетные условия В курсовой работе рассматривается статическая устойчивость узла нагрузки, представленного группой асинхронных двигателей, питающихся от источника питания через внешнюю сеть (рис.3.1). На рис.3.1. представлен один из возможных вариантов схемы электроснабжения узла нагрузки. По заданию преподавателя анализ устойчивости может выполняться для случая, когда выключатели
Рис.3.1. Расчетная схема исследуемой системы
Внешняя питающая сеть при учете лишь индуктивных сопротивлений ее элементов может быть представлена схемой замещения, приведенной на рис.3.2.
Рис. 3.2 Схема замещения внешней питающей сети
Полученная схема замещения питающей сети приводится к расчетному виду (рис.3.3):
Рис. 3.3. Эквивалентная схема замещения внешней сети
При этом эквивалентное сопротивление схемы
Мощность нагрузки Н, подключенной к шинам низшего напряжения трансформаторов Т4, Т5 (рис.3.1) много меньше суммарной мощности асинхронных двигателей, поэтому из расчетной схемы нагрузка Н может быть исключена, т.к. не может существенным образом повлиять на условия обеспечения устойчивости асинхронных двигателей.
Определение параметров Рис.3.4. Последовательные этапы эквивалентирования группы двигателей а – исходная схема, б – промежуточная схема, в – конечная схема
Процедура эквивалентирования состоит из двух этапов. На первом этапе параметры двигателя преобразуются так, чтобы без изменения условий его устойчивости исключить сопротивление реактора
I этап: исключение сопротивлений реактора
Смысл этого преобразования состоит в том, чтобы заменить каждый двигатель, подключенный к шинам с напряжением Условием эквивалентирования является равенство активных и реактивных мощностей, потребляемых от шин Параметры двигателя в схеме, приведенной на рис.3.4,б будем снабжать индексом «¢», чтобы отличить их от исходных. Наличие реактора не изменяет потребляемой из сети активной мощности, поэтому В приближенных расчетах для определения реактивной мощности асинхронного двигателя в номинальном режиме может быть использовано выражение [6]:
где
В схеме, приведенной на рис.3.4,а от общих шин потребляется реактивная мощность
Эквивалентный двигатель в схеме на рис.3.4,б от тех же шин потребляет при номинальной нагрузке реактивную мощность:
Из требований
Величина максимального момента
Номинальное скольжение
Таким образом, определены параметры двигателя в схеме, показанной на рис.3.4,б.
II этап: определение параметров эквивалентного асинхронного двигателя
Рассмотрим методику замены группы из n двигателей, содержащихся в исходной схеме (рис.3.4,б) одним эквивалентным. Критерием эквивалентности является равенство параметров всей группы исходных двигателей и параметров эквивалента при одинаковых скольжениях [6]. 1. Активная, реактивная и полная мощности эквивалентного двигателя определяются по выражениям:
| ||||||||||||||||||||
|
| Поделиться: |


 и соответствующих им взаимных фазовых углов при различных типах автоматических регуляторов возбуждения (АРВ) генераторов электрических станций, определение модулей собственных и взаимных проводимостей системы и углов потерь, расчет и построение характеристик мощности электропередачи, определение предела передаваемой мощности и коэффициентов запаса устойчивости для случаев:
и соответствующих им взаимных фазовых углов при различных типах автоматических регуляторов возбуждения (АРВ) генераторов электрических станций, определение модулей собственных и взаимных проводимостей системы и углов потерь, расчет и построение характеристик мощности электропередачи, определение предела передаваемой мощности и коэффициентов запаса устойчивости для случаев: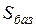 и напряжение
и напряжение  на одной из ступеней трансформации. Тогда на этой ступени трансформации базисное сопротивление будет равно:
на одной из ступеней трансформации. Тогда на этой ступени трансформации базисное сопротивление будет равно: (2.1)
(2.1)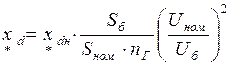 , (2.2)
, (2.2) , (2.3)
, (2.3)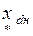 ,
,  - синхронное и переходное индуктивные сопротивления генераторов в относительно номинальных единицах;
- синхронное и переходное индуктивные сопротивления генераторов в относительно номинальных единицах; - номинальная мощность генератора;
- номинальная мощность генератора; - номинальное напряжение генератора;
- номинальное напряжение генератора;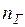 - число генераторов на станции;
- число генераторов на станции; , (2.4)
, (2.4) - напряжение короткого замыкания трансформатора, в %;
- напряжение короткого замыкания трансформатора, в %; , (2.5)
, (2.5)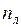 - число цепей;
- число цепей; ,
,  - погонные сопротивления линии, Ом/км;
- погонные сопротивления линии, Ом/км; - длина линии.
- длина линии. и напряжение U)в относительных единицах приводятся к базисным условиям следующим образом:
и напряжение U)в относительных единицах приводятся к базисным условиям следующим образом: , (2.6)
, (2.6)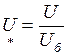 . (2.7)
. (2.7) .
.

 , приложенной за синхронным индуктивным сопротивлением
, приложенной за синхронным индуктивным сопротивлением  , трансформаторы представляются индуктивным сопротивлением
, трансформаторы представляются индуктивным сопротивлением  , линии электропередачи – П-образной схемой замещения (
, линии электропередачи – П-образной схемой замещения ( ,
,  ,
,  ).
). и мощности, выдаваемой с шин генераторной станции
и мощности, выдаваемой с шин генераторной станции 
 . Расчет установившегося режима сети в этом случае, как известно, ведется методом последовательных приближений [13]. На первом этапе выполняется расчет мощностей по участкам сети при допущении, что напряжение в узлах сети равно номинальному. На втором этапе по рассчитанным потокам мощности определяются действительные напряжения в узлах сети и фазовые углы.
. Расчет установившегося режима сети в этом случае, как известно, ведется методом последовательных приближений [13]. На первом этапе выполняется расчет мощностей по участкам сети при допущении, что напряжение в узлах сети равно номинальному. На втором этапе по рассчитанным потокам мощности определяются действительные напряжения в узлах сети и фазовые углы. , (2.8)
, (2.8) ,
,  .
.
 (2.9)
(2.9) ,
, .
. , (2.10)
, (2.10) - характеризует сдвиг вектора
- характеризует сдвиг вектора  относительно вектора напряже-
относительно вектора напряже- .
. , (2.11)
, (2.11)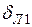 - характеризует сдвиг вектора
- характеризует сдвиг вектора  относительно вектора
относительно вектора  будет равно:
будет равно: , (2.12)
, (2.12) - угол сдвига вектора напряжения на шинах генератора
- угол сдвига вектора напряжения на шинах генератора  , (2.13)
, (2.13) - внутренний угол генератора, характеризующий сдвиг вектора э.д.с.
- внутренний угол генератора, характеризующий сдвиг вектора э.д.с.  относительно вектора напряжения на шинах генератора
относительно вектора напряжения на шинах генератора 
 , равный сумме углов, которые определяют сдвиг по фазе напряжений в начале и в конце каждого из участков С-2, 2-1, 1-Г:
, равный сумме углов, которые определяют сдвиг по фазе напряжений в начале и в конце каждого из участков С-2, 2-1, 1-Г:  .
. , характеризующий сдвиг вектора э.д.с.
, характеризующий сдвиг вектора э.д.с.  .
.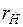 и
и 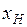 . Значения этих сопротивлений при последовательном их соединении определяются по расчетной мощности
. Значения этих сопротивлений при последовательном их соединении определяются по расчетной мощности 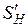 (2.8) и напряжению в узле
(2.8) и напряжению в узле 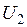 :
: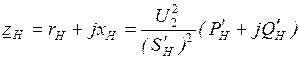 . (2.14)
. (2.14) и
и 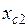 определяются как величины, обратно пропорциональные емкостным проводимостям
определяются как величины, обратно пропорциональные емкостным проводимостям 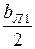 и
и  :
: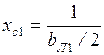 ,
,  (2.15)
(2.15)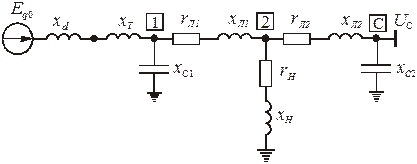
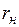 и
и 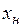
 , (2.16)
, (2.16)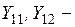 собственные и взаимные проводимости соответственно;
собственные и взаимные проводимости соответственно;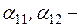 собственные и взаимные углы потерь.
собственные и взаимные углы потерь.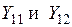 и углов потерь
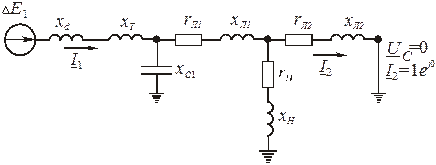
и углов потерь 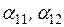 методом единичного тока для схемы замещения, представленной на рис.2.5, напряжение узла С принимают равным нулю -
методом единичного тока для схемы замещения, представленной на рис.2.5, напряжение узла С принимают равным нулю -  , а ток, подтекающий к узлу С, равным единице -
, а ток, подтекающий к узлу С, равным единице - 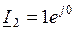 . Преобразованная схема замещения представлена на рис.2.6. Затем определяют напряжение
. Преобразованная схема замещения представлена на рис.2.6. Затем определяют напряжение  , которое должен поддерживать источник напряжения в схеме в таком режиме и ток в ветви этого источника
, которое должен поддерживать источник напряжения в схеме в таком режиме и ток в ветви этого источника 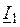 .
.
 методом единичного тока
методом единичного тока по выражениям:
по выражениям: , (2.17)
, (2.17)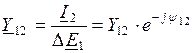 . (2.18)
. (2.18)
 ;
;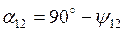 .
. . (2.19)
. (2.19)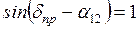 ,
, .
.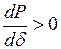 . (2.20)
. (2.20)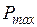 является критическим с точки зрения устойчивости.
является критическим с точки зрения устойчивости. . Если выполняется условие
. Если выполняется условие  , то режим электрической системы при передаче мощности
, то режим электрической системы при передаче мощности 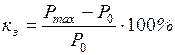 . (2.21)
. (2.21)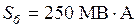 ,
,  кВ.
кВ. кВ.
кВ. ,
, Ом.
Ом. , 2.15) равны:
, 2.15) равны: ,
, ,
,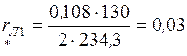 ,
, ,
, ,
, ,
, ,
, .
. ;
;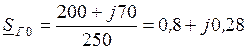 ;
; .
.
 .
. .
. ,
, .
. равна:
равна: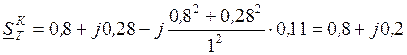 .
. ,
, .
. равна:
равна: ,
, .
. .
. ,
, .
. и
и 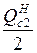 определяется по величине напряжения в узле 2:
определяется по величине напряжения в узле 2: ,
, .
.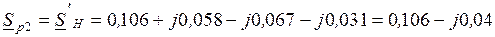 .
. . Согласно (2.14) сопротивление нагрузки равно:
. Согласно (2.14) сопротивление нагрузки равно: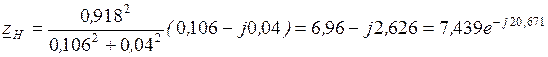 .
. .
. .
.
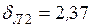 .
. .
. .
. ), равным нулю, а ток, подтекающий к этому узлу, равным единице.
), равным нулю, а ток, подтекающий к этому узлу, равным единице.
 ,
, ,
, ,
, ,
, ,
, ,
,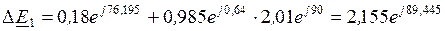 .
.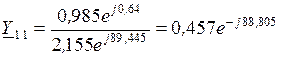 ,
, .
.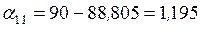 ,
, .
. ,
,  ,
,  ,
,  ,
, 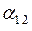 в выражение мощности (2.16) получим:
в выражение мощности (2.16) получим: (2.25)
(2.25) , найденное ранее для нормального установившегося режима, подставим в полученное выражение (2.25) для характеристики мощности:
, найденное ранее для нормального установившегося режима, подставим в полученное выражение (2.25) для характеристики мощности: .
. .
. ,
, .
.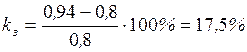 .
. по выражению (2.25). Результаты расчета приведены в табл.2.1. Угловая характеристика мощности представлена на рис.2.10.
по выражению (2.25). Результаты расчета приведены в табл.2.1. Угловая характеристика мощности представлена на рис.2.10.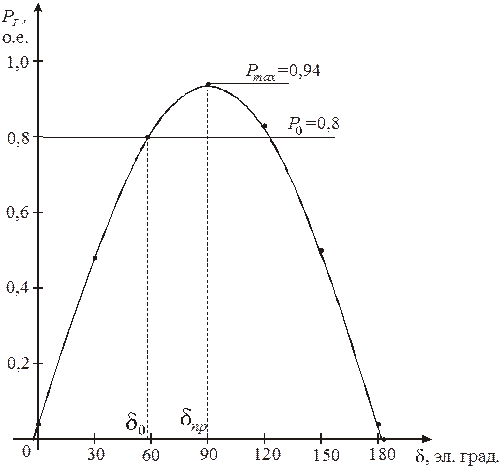
 . Однако коэффициент запаса устойчивости меньше минимально допустимого для нормального режима: 17,5% < 20%. Указанные результаты были получены при отсутствии АРВ генераторов. Обеспечение нормируемого коэффициента запаса возможно при наличии автоматического регулирования возбуждения на генераторах электрической станции.
. Однако коэффициент запаса устойчивости меньше минимально допустимого для нормального режима: 17,5% < 20%. Указанные результаты были получены при отсутствии АРВ генераторов. Обеспечение нормируемого коэффициента запаса возможно при наличии автоматического регулирования возбуждения на генераторах электрической станции. включены, а
включены, а  - отключены, что соответствует, например, условиям ремонтного режима работы трансформатора Т2. В этом случае вся нагрузка питается от одного трансформатора Т1. Также может быть рассмотрен случай подключения узла нагрузки к двум параллельно работающим трансформаторам Т1 и Т2. При определении параметров внешней питающей сети могут быть учтены лишь индуктивные сопротивления ее элементов. Генераторы электрической станции G представляются сопротивлением
- отключены, что соответствует, например, условиям ремонтного режима работы трансформатора Т2. В этом случае вся нагрузка питается от одного трансформатора Т1. Также может быть рассмотрен случай подключения узла нагрузки к двум параллельно работающим трансформаторам Т1 и Т2. При определении параметров внешней питающей сети могут быть учтены лишь индуктивные сопротивления ее элементов. Генераторы электрической станции G представляются сопротивлением  , что соответствует упрощенному учету генераторов с АРВ пропорционального действия в расчетах установившихся режимов.
, что соответствует упрощенному учету генераторов с АРВ пропорционального действия в расчетах установившихся режимов.


 определяется по выражению:
определяется по выражению: (3.1)
(3.1) . Этому соответствует переход к схеме, показанной на рис.3.4,б. На втором этапе выполняется собственно эквивалентирование: свертка схемы и переход к схеме 3.4,в.
. Этому соответствует переход к схеме, показанной на рис.3.4,б. На втором этапе выполняется собственно эквивалентирование: свертка схемы и переход к схеме 3.4,в. через сопротивление реактора
через сопротивление реактора  .
. , (3.2)
, (3.2)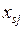 - индуктивное сопротивление рассеяния j -го двигателя;
- индуктивное сопротивление рассеяния j -го двигателя;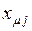 - индуктивное сопротивление ветви намагничивания j -го двигателя.
- индуктивное сопротивление ветви намагничивания j -го двигателя. . (3.3)
. (3.3) .
. , с учетом
, с учетом  , (3.4)
, (3.4) . (3.5)
. (3.5) согласно [6] равна:
согласно [6] равна: . (3.6)
. (3.6) при переходе от схемы на рис.3.4,а к схеме на рис.3.4,б допустимо определять по выражению [6]:
при переходе от схемы на рис.3.4,а к схеме на рис.3.4,б допустимо определять по выражению [6]: . (3.7)
. (3.7) (3.8)
(3.8)


