
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автоматическом регулировании возбуждения генераторовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Расчеты статической устойчивости в зависимости от их назначения проводятся в различном объеме и с различной степенью точности. Современные системы автоматического регулирования возбуждения (АРВ) представляют собой достаточно сложные устройства. Они предназначены для изменения тока возбуждения при изменении режима работы генератора в энергосистеме. Устройства АРВ в зависимости от параметра, на который они реагируют и характера этой реакции разделяются на две большие группы: пропорционального действия АРВ ПД и сильного действия АРВ СД. Автоматические регуляторы возбуждения пропорционального действия реагируют на знак и отклонение напряжения (и тока) от установленного значения. В АРВ СД регулирование возбуждения осуществляется не только по отклонению напряжения, но и по его производной, а также по отклонению и производной каких-либо режимных параметров, т.е. параметров стабилизации, например, частоты. При упрощенных, грубых расчетах устойчивости действие этих устройств отражается введением соответствующих параметров Указанные схемы замещения регулируемых синхронных машин используются при ориентировочных расчетах статической устойчивости, проводимых на стадии проектирования (для выбора номинального напряжения, числа цепей и т.д.), при построении угловых характеристик мощности, определении пропускной способности электропередач, или при эксплуатационных расчетах, когда известно, что возможность самораскачивания в системе исключена. С учетом сказанного расчетная схема замещения исследуемой сети (рис.2.1) при автоматическом регулировании возбуждения генераторов имеет такой же вид, как и при отсутствии АРВ (рис.2.2), с той лишь разницей, что вместо Вычисление э.д.с.
Полный угол электропередачи при использовании на генераторах электростанции АРВ пропорционального действия равен:
Выражения для характеристики мощности генераторной станции при автоматическом регулировании возбуждения генераторов имеют вид: при АРВ ПД:
при АРВ СД:
Проводимости
В курсовой работе следует рассчитать по (2.16), (2.23), (2.24) характеристики мощности для случаев: - отсутствия АРВ на генераторах электрических станций; - при АРВ пропорционального действия; - при АРВ сильного действия. Характеристики мощности Для рассмотренных случаев необходимо сделать заключение об устойчивости системы и об обеспечении требуемых запасов по устойчивости. Следует пояснить влияние автоматического регулирования возбуждения на статическую устойчивость электрических систем. Пример 2.1. Электропередача напряжением
Рис.2.7. Расчетная схема системы
Параметры элементов электрической системы. Генераторы G1, G2: ТВФ-100,
Трансформаторы Т1, Т2:
Линии электропередачи: W1 W2
Заданные параметры исходного режима: напряжение на шинах генератора Требуется: 1. Рассчитать параметры исходного установившегося режима работы электрической системы (рис.2.7): определить величины напряжений в узлах сети, э.д.с. генератора
2. Определить собственные и взаимные проводимости 3. Рассчитать и построить характеристику мощности электропередачи. 4. Определить предел передаваемой мощности и коэффициент запаса устойчивости.
Решение. При отсутствии АРВ генераторов, представлении линии П-образной схемой замещении, неучете активных сопротивлений трансформаторов и их ветвей намагничивания, схема замещения рассматриваемой системы имеет вид, изображенный на рис.2.2. Определим параметры схемы замещения в относительных единицах. Примем в качестве базисных условий: Базисное напряжение на ступени 220 кВ составит:
Базисное сопротивление на ступени 220 кВ равно:
При принятых базисных условиях параметры схемы замещения в соответствии с (
Определим заданные параметры режима в относительных единицах. Напряжение на шинах эквивалентного генератора:
В дальнейшем в расчетах используются параметры, приведенные к базисным условиям, обозначение «*» для краткости опускается. Мощность, выдаваемая с шин генераторной станции:
Мощность нагрузки:
Полученные данные нанесем на схему замещения (рис.2.8).
Рис.2.8. К примеру 2.1. Схема замещения электрической системы
Определим э.д.с. генераторной станции по выражению (2.13):
Внутренний угол генератора равен
Напряжение в узле 1 равно:
Мощность
Зарядная мощность в начале линии W1 определяется величиной напряжения в узле 1:
Мощность
Мощность конца линии 1 – 2:
Напряжение в узле 2 равно:
Зарядные мощности
Найдем расчетную мощность узла 2:
Емкостной характер расчетной мощности обусловлен превышением суммарной зарядной мощности линий 220 кВ, примыкающих к узлу 2, над реактивной мощностью нагрузки. Представим расчетную нагрузку неизменным сопротивлением
Мощность начала линии W2 равна
Мощность конца этой линии равна:
Напряжение на шинах приемной системы равно:
Внешний угол электропередачи равен сумме углов
Полный угол электропередачи равен сумме внутреннего
Определим собственные и взаимные проводимости методом единичного тока. С этой целью рассчитаем распределение токов и напряжений в рассматриваемой схеме, приняв напряжение второго источника питания ( Расчетная схема замещения для расчета проводимостей методом единичного тока представлена на рис.2.9.
Рис. 2.9. К примеру 2.1. Расчетная схема для расчета собственных и взаимных проводимостей
В результате последовательного расчета режима такой схемы находим:
Собственные и взаимные проводимости в соответствии с (2.17), (2.18) равны:
Собственные и взаимные углы потерь равны:
Подставив полученные значения
Для проверки вычислим активную мощность в исходном режиме. С этой целью значение полного угла электропередачи
Результат вычислений совпал с заданным значением активной мощности генераторной станции, следовательно расчеты выполнены верно. Предел передаваемой мощности находится как максимум полученной характеристики мощности:
Полный угол электропередачи, соответствующий этому пределу, определим из соотношения:
Коэффициент запаса статической устойчивости согласно (2.21) равен:
Для построения угловой характеристики вычислим значения мощности при различных углах
Табл.2.1 Результаты расчета мощности генераторной станции при различных углах
Рис. 2.10. Угловая характеристика мощности электропередачи
Вывод: статическая устойчивость рассматриваемой системы при заданных условиях обеспечивается, поскольку полный угол электропередачи в исходном режиме меньше предельного:
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 3184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.131.115 (0.011 с.) |

 и
и  в простейшую схему замещения синхронной машины. Генераторы с АРВ пропорционального действия замещаются э.д.с.
в простейшую схему замещения синхронной машины. Генераторы с АРВ пропорционального действия замещаются э.д.с.  (
( ) приложенной за сопротивлением
) приложенной за сопротивлением  , а при сильном регулировании возбуждения такие расчеты выполняются при
, а при сильном регулировании возбуждения такие расчеты выполняются при  и
и 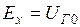 , т.е. при неизменном напряжении на шинах генератора.
, т.е. при неизменном напряжении на шинах генератора. и сопротивления
и сопротивления  используется э.д.с.
используется э.д.с.  .
. . (2.22)
. (2.22) .
. ; (2.23)
; (2.23) . (2.24)
. (2.24) ,
,  и углы потерь
и углы потерь  ,
,  в выражениях (2.23) и (2.24) определяются для соответствующих расчетных схем:
в выражениях (2.23) и (2.24) определяются для соответствующих расчетных схем: при замещении генератора сопротивлением
при замещении генератора сопротивлением  при исключении из расчетной схемы сопротивления генератора
при исключении из расчетной схемы сопротивления генератора  .
. для всех рассмотренных случаев для большей наглядности должны быть построены на одном рисунке. Для всех трех случаев должен быть определен предел передаваемой мощности, предельный угол электропередачи и коэффициент запаса статической устойчивости по активной мощности по выражению (2.21). Также следует выполнить проверку правильности расчетов: при подстановке полного угла электропередачи в выражение для характеристики мощности должно получиться значение заданной активной мощности генераторной станции.
для всех рассмотренных случаев для большей наглядности должны быть построены на одном рисунке. Для всех трех случаев должен быть определен предел передаваемой мощности, предельный угол электропередачи и коэффициент запаса статической устойчивости по активной мощности по выражению (2.21). Также следует выполнить проверку правильности расчетов: при подстановке полного угла электропередачи в выражение для характеристики мощности должно получиться значение заданной активной мощности генераторной станции. кВ, связывающая электрическую станцию (
кВ, связывающая электрическую станцию ( ) с системой бесконечной мощности (С), имеет промежуточную подстанцию, мощность которой составляет
) с системой бесконечной мощности (С), имеет промежуточную подстанцию, мощность которой составляет  . Расчетная схема исследуемой системы приведена на рис.2.7.
. Расчетная схема исследуемой системы приведена на рис.2.7.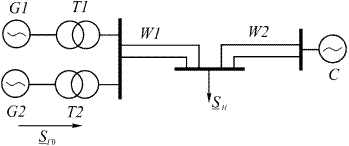
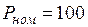 МВт,
МВт,  ,
, ,
,  ,
,  кВ.
кВ. ,
, 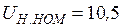 кВ,
кВ, кВ,
кВ, 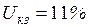 .
.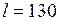 км АСО-300
км АСО-300 км АСО-300
км АСО-300 Ом/км,
Ом/км,  Ом/км,
Ом/км, .
. кВ, мощность, передаваемая с шин генераторной станции составляет
кВ, мощность, передаваемая с шин генераторной станции составляет  .
. и углы потерь
и углы потерь 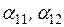 .
.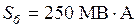 ,
,  кВ.
кВ. кВ.
кВ. ,
, Ом.
Ом. , 2.15) равны:
, 2.15) равны: ,
, ,
,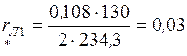 ,
, ,
, ,
, ,
, ,
, .
. ;
;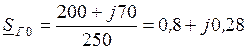 ;
; .
.
 .
. .
. ,
, .
. равна:
равна: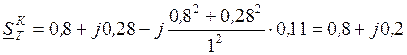 .
. ,
, .
. равна:
равна: ,
, .
. .
.
 ,
, .
. и
и 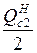 определяется по величине напряжения в узле 2:
определяется по величине напряжения в узле 2: ,
, .
.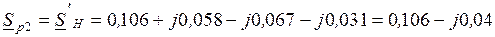 .
. . Согласно (2.14) сопротивление нагрузки равно:
. Согласно (2.14) сопротивление нагрузки равно: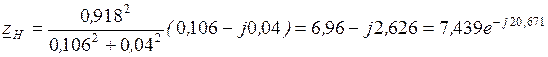 .
. .
. .
.
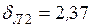 .
. ,
, 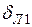 ,
, 
 .
. и внешнего
и внешнего  углов:
углов: .
. ), равным нулю, а ток, подтекающий к этому узлу, равным единице.
), равным нулю, а ток, подтекающий к этому узлу, равным единице.
 ,
, ,
, ,
, ,
, ,
, ,
,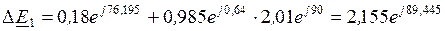 .
.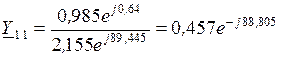 ,
, .
.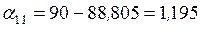 ,
, .
. ,
,  ,
,  ,
,  ,
, 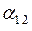 в выражение мощности (2.16) получим:
в выражение мощности (2.16) получим: (2.25)
(2.25) , найденное ранее для нормального установившегося режима, подставим в полученное выражение (2.25) для характеристики мощности:
, найденное ранее для нормального установившегося режима, подставим в полученное выражение (2.25) для характеристики мощности: .
. .
. ,
, .
.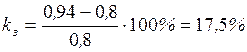 .
. по выражению (2.25). Результаты расчета приведены в табл.2.1. Угловая характеристика мощности представлена на рис.2.10.
по выражению (2.25). Результаты расчета приведены в табл.2.1. Угловая характеристика мощности представлена на рис.2.10.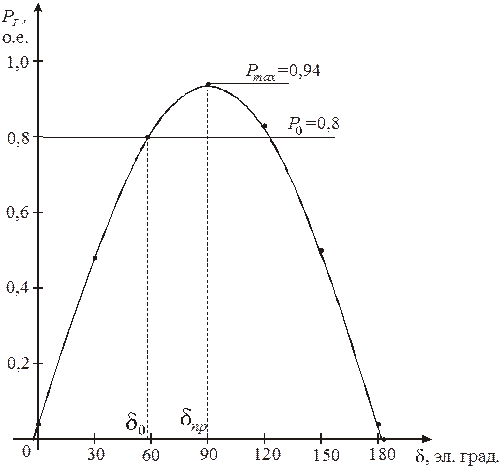
 . Однако коэффициент запаса устойчивости меньше минимально допустимого для нормального режима: 17,5% < 20%. Указанные результаты были получены при отсутствии АРВ генераторов. Обеспечение нормируемого коэффициента запаса возможно при наличии автоматического регулирования возбуждения на генераторах электрической станции.
. Однако коэффициент запаса устойчивости меньше минимально допустимого для нормального режима: 17,5% < 20%. Указанные результаты были получены при отсутствии АРВ генераторов. Обеспечение нормируемого коэффициента запаса возможно при наличии автоматического регулирования возбуждения на генераторах электрической станции.


