
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение параметров исходного режимаСодержание книги
Поиск на нашем сайте
Электрической системы
Под статической устойчивостью электрической системы понимается ее способность возвращаться к установившемуся режиму после его малых возмущений. Малые возмущения могут возникать в результате изменений режимов работы электрической системы, например, отключения части питающих линий, при оперативных переключениях и т.п. Для расчета и анализа переходных процессов в электрической системе предварительно выполняется расчет исходного установившегося режима ее работы, возмущение этого режима и будет вызывать рассматриваемый переходный процесс. Расчет исходного установившегося режима выполняется с целью определения его параметров: напряжений в узлах сети, э.д.с. генераторных станций и фазовых углов, потоков мощности по участкам сети. Расчеты производятся на основании схемы замещения электрической системы. Расчетная схема замещения электрической системы составляется из схем замещения отдельных элементов системы (генераторов, трансформаторов, линий и т.д.), связанных друг с другом так же, как соединены соответствующие элементы рассматриваемой системы. Расчеты переходных электромеханических процессов удобно выполнять в системе относительных единиц. При этом как параметры элементов схемы замещения системы (сопротивления контуров), так и параметры режима (э.д.с., напряжения, мощности) выражаются в долях от соответствующих величин, принятых за базисные. В качестве таких величин обычно принимают мощность
На других ступенях трансформации базисные напряжения пересчитываются с учетом действительных коэффициентов трансформации трансформаторов к рассматриваемой ступени. Параметры эквивалентных элементов электрической системы определяются по следующим выражениям: - сопротивления генераторов
где
- сопротивления трансформаторов
где
- сопротивления линий
где
Заданные параметры режима (мощность
Рассмотрим определение параметров исходного режима для простейшей схемы выдачи мощности генераторной станции на шины приемной системы бесконечной мощности (рис. 2.1). В системе имеется промежуточный отбор мощности. Мощность нагрузки
Рис. 2.1. Расчетная схема исследуемой системы
Схема замещения рассматриваемой системы при отсутствии АРВ генераторов электрической станции представлена на рисунке 2.2.
Рис. 2.2. Схема замещения расчетной системы
При составлении схемы замещения генераторы без АРВ замещаются э.д.с. Рассмотрим расчет исходного режима при следующих заданных его параметрах: напряжении на шинах системы Предварительно определим расчетную мощность в узле 2:
где Схема замещения преобразуется к виду:
Рис. 2.3. Схема замещения исследуемой системы после преобразования по (2.8)
Расчет потоков мощности по участкам сети выполняется от начала электропередачи к ее концу по следующим выражениям:
На втором этапе при заданном напряжении на шинах приемной системы с учетом потоков мощности, определенных на первом этапе по выражениям (2.9), определяются напряжения в каждой узловой точке сети. При совмещении вектора
где угол ния шин системы Совместив вектор
где угол При совмещении вектора
где Э.д.с. генераторной станции равна:
где Векторная диаграмма напряжений и э.д.с. генератора представлена на рис. 2.4.
Рис. 2.4. Векторная диаграмма напряжений и э.д.с.
Из рисунка 2.4 видно, что напряжения в узлах Полный угол электропередачи
|
||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 194; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.209.66 (0.01 с.) |

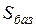 и напряжение
и напряжение  на одной из ступеней трансформации. Тогда на этой ступени трансформации базисное сопротивление будет равно:
на одной из ступеней трансформации. Тогда на этой ступени трансформации базисное сопротивление будет равно: (2.1)
(2.1)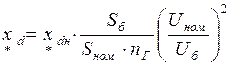 , (2.2)
, (2.2) , (2.3)
, (2.3)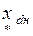 ,
,  - синхронное и переходное индуктивные сопротивления генераторов в относительно номинальных единицах;
- синхронное и переходное индуктивные сопротивления генераторов в относительно номинальных единицах; - номинальная мощность генератора;
- номинальная мощность генератора; - номинальное напряжение генератора;
- номинальное напряжение генератора;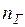 - число генераторов на станции;
- число генераторов на станции; , (2.4)
, (2.4) - напряжение короткого замыкания трансформатора, в %;
- напряжение короткого замыкания трансформатора, в %; , (2.5)
, (2.5)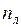 - число цепей;
- число цепей; ,
,  - погонные сопротивления линии, Ом/км;
- погонные сопротивления линии, Ом/км; - длина линии.
- длина линии. и напряжение U)в относительных единицах приводятся к базисным условиям следующим образом:
и напряжение U)в относительных единицах приводятся к базисным условиям следующим образом: , (2.6)
, (2.6)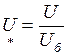 . (2.7)
. (2.7) .
.

 , приложенной за синхронным индуктивным сопротивлением
, приложенной за синхронным индуктивным сопротивлением  , трансформаторы представляются индуктивным сопротивлением
, трансформаторы представляются индуктивным сопротивлением  , линии электропередачи – П-образной схемой замещения (
, линии электропередачи – П-образной схемой замещения ( ,
,  ,
,  ).
). и мощности, выдаваемой с шин генераторной станции
и мощности, выдаваемой с шин генераторной станции 
 . Расчет установившегося режима сети в этом случае, как известно, ведется методом последовательных приближений [13]. На первом этапе выполняется расчет мощностей по участкам сети при допущении, что напряжение в узлах сети равно номинальному. На втором этапе по рассчитанным потокам мощности определяются действительные напряжения в узлах сети и фазовые углы.
. Расчет установившегося режима сети в этом случае, как известно, ведется методом последовательных приближений [13]. На первом этапе выполняется расчет мощностей по участкам сети при допущении, что напряжение в узлах сети равно номинальному. На втором этапе по рассчитанным потокам мощности определяются действительные напряжения в узлах сети и фазовые углы. , (2.8)
, (2.8) ,
,  .
.
 (2.9)
(2.9) ,
, .
. , (2.10)
, (2.10) - характеризует сдвиг вектора
- характеризует сдвиг вектора  относительно вектора напряже-
относительно вектора напряже- .
. , (2.11)
, (2.11)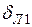 - характеризует сдвиг вектора
- характеризует сдвиг вектора  относительно вектора
относительно вектора  будет равно:
будет равно: , (2.12)
, (2.12) - угол сдвига вектора напряжения на шинах генератора
- угол сдвига вектора напряжения на шинах генератора  , (2.13)
, (2.13) - внутренний угол генератора, характеризующий сдвиг вектора э.д.с.
- внутренний угол генератора, характеризующий сдвиг вектора э.д.с.  относительно вектора напряжения на шинах генератора
относительно вектора напряжения на шинах генератора 
 , равный сумме углов, которые определяют сдвиг по фазе напряжений в начале и в конце каждого из участков С-2, 2-1, 1-Г:
, равный сумме углов, которые определяют сдвиг по фазе напряжений в начале и в конце каждого из участков С-2, 2-1, 1-Г:  .
. , характеризующий сдвиг вектора э.д.с.
, характеризующий сдвиг вектора э.д.с.  .
.


