
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определить с помощью таблиц истинности, является ли приведенная формула алгебры высказывание тавтологиейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте (а \/ b)
В последнем столбце построенной для данной формулы таблицы истинности при всех наборах значений переменных ходящих в нее простых высказываний получены только значения истины, следовательно, она является тавтологией.
Применение основных равносильностей алгебры высказываний для решения содержательных задач
Перевод некоторых (наиболее часто встречающихся) выражений естественного языка на символический язык алгебры логики
Рассмотрим на примере, как используются приведенные выше равносильности алгебры высказываний при решении содержательных задач. Задача: В замке есть две комнаты, в каждой из которых может находиться либо тигр, либо принцесса. На дверях комнат имеются таблички следующего содержания: табличка I - «По крайней мере в одной из комнат находится принцесса», табличка II – «Принцесса находится в другой комнате». Если в первой комнате находится принцесса, то утверждение на табличке I истинно, если тигр – то ложно. Для второй комнаты наоборот, если там находится принцесса, то утверждение на табличке II ложно, а если там находится тигр – то это утверждение истинно. Определить, в какой из комнат находится принцесса. Решение: Введем обозначения для простых высказываний, необходимые для формализации условия задачи, обозначив соответственно через П1 высказывание «принцесса находится в первой комнате», через П2 - высказывание «принцесса находиться во второй комнате», тогда высказывание «тигр находится в первой комнате» есть отрицание переменной П1, а высказывание «тигр находится во второй комнате» - отрицание высказывания П2. Тогда надпись на первой двери (обозначим это сложное суждение через А) можно представить в виде конъюнкции высказываний П1 и П2 (А=П1 Учитывая условие, что при нахождении в первой комнате принцессы утверждение на табличке I истинно, тигра – то ложно, а для второй комнаты при нахождении в ней принцессы утверждение на табличке II ложно, нахождения в ней тигра это утверждение истинно, получим в формализованном виде следующую запись условия нашей задачи:
(П1*А =(П1*(П1 = П1* П2. 1. П1*(П1 = П1*П2
2. (П2*П1 = П2*П1*П1 = П1* П2.
Замечание: жирным шрифтом здесь отмечены нулевые конъюнкции, С учетом введенных обозначений для переменных П1 и П2 (П1- «принцесса находится в первой комнате», П2 – «принцесса находится во второй комнате») и полученной в результате преобразований формуле П1* П2 можем сформулировать ответ на вопрос задачи – принцесса находится в первой комнате.
Примеры: а) Проверьте равносильность двумя способами:
Первый способ проверки равносильностей - при помощи построения таблиц истинности ля левой и правой части формулы. Если истинностные значения в соответствующих столбцах совпадают при любых наборах значений составляющих простых суждений, то равносильность считается доказанной, в противном случае она не имеет места. Составим таблицы истинности для левой и правой частей приведенной формулы (табл. 2, табл.3):
Таблица 2
Второй способ проверки равносильностей алгебры логики- преобразование исходной формулы на основании известных. Ранее доказанных основных равносильностей алгебры высказываний.
Используем для доказательства метод приведения левой части фрмулы к правой: 1) 2) 3) 4) Так как левая часть в результате равносильных преобразований не эквивалентна правой, можно сделать вывод, о том, что данная формула не является равносильностью алгебры высказываний.
в) Найдите отрицание приведенного сложного высказывания: Если урок будет интересным, никто из мальчиков — Петя, Ваня, Коля — не будет смотреть в окно; Ведем обозначения для простых суждений, входящих в состав приведенного сложного суждения и воспользуемся общим правилом отрицания сложных суждений. Пусть П - суждение «Петя посмотрит в окно», В - суждение «Ваня посмотрит в окно», К - суждение «Коля посмотрит в окно», И – «урок будет интересным». Тогда, формализуя исходное сложное суждение и учитывая, что нужно найти его отрицание, получим: (И→ ПВК)↔ И*(П+В+Л) Следовательно, отрицание исходного сложного суждения можно сформулировать в виде: «Урок будет интересным, но хотя бы один их мальчиков (Петя, Ваня, Коля) будет смотреть в окно». Аудиторная самостоятельная работа №10 «Применение основных равносильностей алгебры высказываний К решению задач» Задание №1. Одна жительница древних Афин предостерегала сына: «Если ты будешь говорить правду, тебя возненавидят люди, а если ты будешь лгать, тебя возненавидят боги. Но ты должен или говорить правду, или лгать. Значит, тебя возненавидят люди или тебя возненавидят боги». Сын ответил матери: «Если я буду говорить правду, меня полюбят боги, а если буду лгать — меня полюбят люди. Но я должен или говорить правду, или лгать. Значит, меня полюбят или боги, или люди». Кто из них прав? (решить задачу двумя способами) Указание: для доказательства удобно принять следующие обозначения: сын будет говорить правду — П, сын будет лгать -
(максимальное количество баллов – 10)
Задание №2. Проверьте следующие равносильности двумя способами: а) б) в) г)
(максимальное количество баллов – 40)
Задание №3. Проверьте следующие равносильности, используя основные равносильности алгебры логики (предварительно упростив выражения, заключенные в скобки): а) б) в) г) (максимальное количество баллов – 20) Задание №4. Перевести на язык алгебры логики следующие высказывания: 1. Если светит солнце, то для того, чтобы не было дождя, достаточно, чтобы дул ветер; 2. Неверно, что если дует ветер, то солнце светит только тогда, когда нет дождя; 3. Чтобы погода была солнечной, достаточно, чтобы не было ни ветра, ни дождя; 4. Если ветра нет, то для дождя необходима пасмурная погода; 5. Если погода пасмурная и дует ветер, то дождя нет, но дождь идет, значит, нет ветра; 6. Неверно, что если погода пасмурная, то дождь идет тогда и только тогда, когда нет ветра; 7. Если для солнечной погоды необходимо отсутствие дождя, то для того, чтобы пошел дождь, достаточно, чтобы погода была пасмурной и безветренной; 8. Будет ветреная погода, разве что пойдет дождь; 9. Дождь идет только тогда, когда погода пасмурная и безветренная, но дождя нет, значит, погода либо солнечная, либо пасмурная и ветреная; 10. Погода не только солнечная, но и безветренная, значит, дождя не будет, если не поднимется ветер; 11. Пойдет дождь, разве что поднимется ветер, значит, погода будет либо солнечной, либо пасмурной и ветреной; 12. Погода будет не только пасмурной, но и дождливой, несмотря на ветер. Значит, солнечной погоды не будет, разве что прекратится дождь.
(максимальное количество баллов – 60)
Указание: нужно каждый раз предварительно выделить элементарные высказывания и обозначить их заглавными буквами. Буквы удобнее всего выбирать так, чтобы всегда можно было бы быстро восстановить полный текст составного высказывания. Например: «светит солнце» можно обозначить буквой С, «дует ветер» — буквой В, «идет дождь» — буквой Д, «погода пасмурная» — буквой П.
Задание №5. Найдите отрицания следующих сложных высказываний: 1. Если пойдет дождь, Ваня, Петя и Коля останутся дома; 2. Коля решит задачу, если он вспомнит нужную теорему; 3. Хотя бы один из мальчиков (Ваня, Петя, Коля)-ошибается; 4. Ни один из мальчиков (Ваня, Петя, Коля) не опоздал в школу; 5. В кино пойдет либо Коля, либо Петя; 6. Если урок будет интересным, никто из мальчиков — Петя, Ваня, Коля — не будет смотреть в окно; 7. Будет солнечная погода, но хотя бы один из мальчиков — Петя и Ваня — не пойдет в лес; 8. Учитель рассказал смешную историю,но ник учеников — Петя и Ваня — не засмеялся; 9. Погода будет пасмурной, и Ваня пойдет в леси только тогда, когда в лес пойдет Коля; 10. Петя будет купаться только при солнечной погоде, если будет жарко. (максимальное количество баллов – 50)
Указание: В высказываниях 7—9 ответ представить в виде импликации. Домашняя самостоятельная работа №6 «Применение основных равносильностей алгебры высказываний К решению задач» Примечание: каждая из задач данной работы оценивается в 10 баллов. Задание №1. На вопрос, какая погода будет завтра, синоптик ответил: 1) Если будет мороз, то снег выпадет только пасмурной погоде. 2) Если не будет мороза,но пойдет снег, то погода будет пасмурной. 3) Не будет ни снега, ни дождя, если небо будет ясным. 4) Неверно,что если не будетмороза, то для выпадения снега или дождя достаточно наличия пасмурного неба. Какую погоду предсказал синоптик? Задание №2. Петя хочет погулять, но на улице собирается дождь. У него возникают следующие соображения: 1) Если я надену плащ, то, для того чтобы я надел еще и сапоги, необходимо, чтобы пошел дождь. 2) Если я надену сапоги или галоши, но не будет дождя, то плащ надевать не надо. 3) Неверно, что если я не надену плащ, то я обойдусь без сапог и без галош только тогда, когда не будет дождя. 4) Для того, чтобы я не надел ни сапог, ни галош, ни плаща, достаточно, чтобы не было дождя. К какому выводу привели Петю эти соображения? Задание №3. Андрей, Ваня и Саша собрались в поход. Учитель, хорошо знавший этих ребят, высказал следующие предположения: 1) Андрей пойдет в поход только тогда, когда пойдут Ваня и Саша. 2) Андрей и Саша друзья, а это значит, что они поход или вместе или же оба останутся дома. 3) Чтобы Саша пошел в поход, необходимо, чтобы пошел Ваня. Когда ребята пошли в поход, оказалось, что учитель немного ошибся: из трех его утверждений истинными оказались только два. Кто из названных ребят пошел в поход? Задание №4. Петя решил поступить в МГУ и послал домой три сообщения: 1) Если я сдам математику» то физику я сдамтолькопри условии, что не завалю сочинение. 2) Не может быть, чтобы я завалил и сочинение и математику. 3)Достаточное условие завала по физике — это двойка по сочинению. После сдачи экзаменов оказалось, что, из трех Петиных сообщений,только одно было ложным.Как Петя слад экзамены? Задание №5. Коля пригласил свою сестру приехать к нему в гости. После этого он получил от нее три сообщения: 1) Я приеду в гости, если только со мной поедет папа. 2) Чтобы я приехала, необходимо, чтобы меня сопровождала мама. 3)Либо приедем мы с мамой, либо приедет только папа. Когда приехали гости, оказалось, что из этих трех сообщений истинным было только одно. Кто приехал навестить Колю? Задание №6. У разбойника, посаженного в тюрьму, было три сообщника. От каждого из них он получил по одному сообщению: 1) Для того чтобы твой побег состоялся, достаточно, чтобы стража была подкуплена только тогда, когда будет окончено рытье подкопа». 2) Если стража будет подкуплена, то достаточное условие твоего побега будет состоять в своевременном окончании рытья подкопа. 3) Если рытье подкопа будет закончено, то необходимо подкупить стражу. Но стражу подкупить не удается. Значит, побег невозможен. Разбойник знал, что только один из его сообщников говорит правду, а остальные всегда врут. Значит, из полученных трех сообщений истинно только одно Какую информацию получил разбойник? Задание №7. Разбойник, посаженный в тюрьму, послал своим сообщникам две записки: 1) Для побега достаточно, чтобы стража была подкуплена только тогда, когда вам удастся передать мне веревочную лестницу. 2) Для совершения побега необходимо, чтобы стража была подкуплена и мне была передана веревочная лестница. На следующий день разбойник опять послал своим сообщникам две записки. Первая записка была похожа на предыдущие: 1)Если будет подкуплена стража, то для совершения побега достаточно передать мне веревочную лестницу. Вторая же записка была полна пессимизма: 2) Невозможно, чтобы стража была подкуплена, мне была передана лестница и побег удался. На третий день разбойник получил ответ: «Из каждой пары твоих высказываний истинно только одно». Какую информацию получил разбойник? Задание №8. Совершено убийство. Подозреваются Браун, Джон, Смит. Один из них брат убитого. Другой - сосед, а третий—случайный знакомый. Каждый из них сделал заявление. Браун: Если ни я, ни Джон невиновны, то Смит невиновен. Смит: Чтобы обвинить меня и Брауна, достаточно признать Джона невиновным. Но Джон виновен. Значит, нельзя считать, что ни я, ни Браун невиновны. Джон: Если меня сочтут виновным, то Смиту удастся оправдаться только тогда, когда оправдается Браун. Но виновен либо Смит, либо Браун. А я невиновен. Следователь сообщил, что правду сказал только брат убитого, а остальные подозреваемые солгали. Кто убийца? Задание №9. В школьном шахматном турнире участвовалиИванов, Петров и Сидоров. Отца одного из них попросили быть судьей на турнире. Перед началом турнира его участники высказали следующие предположения: Ивановв: Не может быть, чтобы победили Петров и Сидоров вместе. Не может быть также, чтобы победил либо Петров, либо Сидоров. Значит, не смогу быть победителем и я. Петров: Если Иванов проиграет, то Петров будет победителем только тогда, когда выяснится, что Сидоров проиграл. Если Иванов проиграет, то проиграет, и Сидоров. А я выиграть не смогу. Сидоров: Не может быть, чтобы проиграли и Иванов, в Петров, а я бы победил. После окончания турнира судья сказал, что подтвердилось только высказывание его сына, а остальные высказывания оказались неверными. Кто был победителем турнира? Как фамилия судьи? Задание №10. Было совершено ограбление. Мегрэ сообщили, что подозреваются трое бродяг: Луи, Франсуа и Этьен. Бродяги дали следующие показания: Луи: Чтобы обвинить меня, достаточно доказать,чтоФрансуа участвует в ограблении толькотогда, когда в нем участвует Этьен, но я невиновен. Франсуа: Если Луи невиновен, то, чтобы обвинить меня, достаточно признать Этьена тоже невиновным. Но Этьен виновен тогда и только тогда, когда виновен Луи. А если Этьен виновен, то я невиновен. Этьен: Виновен либо я, либо Франсуа и Луи. Мегре знал, что Этьен всегда лжет, а Луи и Франсуа говорят правду. Это помогло ему распутать дело. Кто был причастен к ограблению?
Указание: При решении всех задач надо обходиться минимальным количеством переменных. Поэтому если высказывание «Погода будет пасмурной» обозначено буквой П, то противоположное высказывание «Погода будет ясной» следует обозначить через Тема 4 (продолжение) Информационный материал
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 4057; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.129.125 (0.014 с.) |

 (а
(а  b)
b)

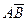






 П2), а надпись на второй двери (обозначим его через В) совпадает с высказыванием П1, т.е. В=П1.
П2), а надпись на второй двери (обозначим его через В) совпадает с высказыванием П1, т.е. В=П1. П1*А)*(П2*В
П1*А)*(П2*В 
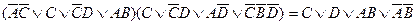
 ;
; ;
; ;
; ≠
≠  .
. ; сына полюбят люди — Л, сына возненавидят люди -
; сына полюбят люди — Л, сына возненавидят люди -  ; сына полюбят боги—Б, сына возненавидят боги -
; сына полюбят боги—Б, сына возненавидят боги -  .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
;


