
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Если днф является трехчленом, зависящим от трех переменных, и если симметрия нарушена только по одной из переменных, то пропадает тот член дизъюнкции, который эту переменную не содержит.Содержание книги
Поиск на нашем сайте
Проиллюстрируем это правило еще на двух примерах. 1. 2. Минимальной мы назовемту ДНФ, которая имеет самую короткую запись. Существует еще одно правило поглощения, которое тоже основано на соображениях симметрии: Если ДНФ является трехчленом, зависящим от трех переменных, и если симметрия нарушена по двум из этих переменных, то данная ДНФ равносильна дизъюнкции, одним из членов которой является переменная, по которой симметрия не нарушена, а вторым членом служит тот член первоначальной ДНФ, который эту переменную не содержит. Например:
Рассмотрим еще несколько примеров, иллюстрирующих это правило. 1. 2. Для каждой формулы существует бесконечно много различных, но равносильных ей ДНФ. Если, например, найдена одна ДНФ, то путем повторения имеющихся элементарных конъюнкций, добавления нулевых конъюнкций, добавления поглощаемых конъюнкций можно построить бесконечно много новых, но равносильных ей ДНФ. Например: Среди всех этих ДНФ есть одна, которая отличаете однородностью и «совершенством» своей формы. Mы имеем в виду формулу: Дадим точное определение: СДНФ — это такая ДНФ, которая удовлетворяет следующим условиям: 1. Все элементарные конъюнкции различны. 2. Нет нулевых конъюнкций. 3. Ни одна из элементарных конъюнкций не содержит одинаковых членов. 4. Каждая элементарная конъюнкция содержит все переменные.
Чтобы получить СДНФ, надо сначала найти минимальную ДНФ. Тогда будут выполнены условия 1, 2, 3. Посли этого надо преобразовать эту минимальную ДНФ таким образом, чтобы было выполнено условие 4. Это делается следующим образом:
Элементарной дизъюнкцией называется дизъюнкция, состоящая только из переменных или их отрицаний. Например: Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций. Например: Но эта формула не является еще минимальной. Для КНФ тоже существуют правила поглощения, основанные на соображениях симметрии. Эти правила можно получить по закону двойственности из аналогичных правил, установленных для ДНФ. Мы знаем, например, что: В то же время мы установили новое правило поглощения: Если КНФ зависит от трех переменных и представляет собой конъюнкцию трех элементарных дизъюнкций и если симметрия нарушена только по одной из переменных, то поглощается та элементарная дизъюнкция, которая эту переменную не содержит. Аналогичным образом можно получить и второе правило поглощения, основанное на соображениях симметрии. Мы уже знаем, что: Запишем двойственную равносильность: Сформулируем соответствующее правило поглощения: Если КНФ зависит от трех переменных и представляет собой конъюнкцию трех элементарных дизъюнкций и если симметрия нарушена по двум из этих переменных, то данная КНФ равносильна конъюнкции, одним из членов которой является переменная, по которой симметрия не нарушена, а вторым членом является тот член первоначальной КНФ, который эту переменную не содержит.
Чтобы найти минимальную КНФ, равносильную данной формуле, надо эту формулу сначала привести к виду ДНФ, затем надо разложить ее на «множители» и применить законы поглощения. Рассмотрим конкретный пример.
Можно поступить и по-другому. Новый подход начнется с того момента, когда была получена формула
Мы получили тот же ответ.
|
||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.193.71 (0.01 с.) |

 . Этот трехчлен содержит два раза
. Этот трехчлен содержит два раза  , два раза
, два раза  , но один раз
, но один раз  и один раз
и один раз  . Значит,, симметрия нарушена по
. Значит,, симметрия нарушена по  .
. . Этот трехчлен содержит два раза
. Этот трехчлен содержит два раза  , два раза
, два раза 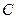 и один раз
и один раз  . Симметрия нарушена по
. Симметрия нарушена по  .
. . Покажем, что это действительно так:
. Покажем, что это действительно так:
 .
.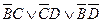 . Этот трехчлен содержит два раза
. Этот трехчлен содержит два раза  .
. . В этом трехчлене симметрия нарушена по
. В этом трехчлене симметрия нарушена по  . Значит,
. Значит,  .
.
 Она так и называется: «совершенная дизъюнктивно-нормальная форма» (СДНФ).
Она так и называется: «совершенная дизъюнктивно-нормальная форма» (СДНФ). Приведение формул алгебры высказываний к КНФ виду
Приведение формул алгебры высказываний к КНФ виду .
. . Если воспользоваться равносильностью
. Если воспользоваться равносильностью  , то
, то  можно заменить через
можно заменить через  . Кроме того, известно, что,
. Кроме того, известно, что, 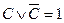 . А если один член дизъюнкции равен 1, то и вся дизъюнкция равна 1. Значит:
. А если один член дизъюнкции равен 1, то и вся дизъюнкция равна 1. Значит: 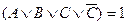 . Но
. Но 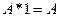 . Значит, единичный член конъюнкции можно просто опустить. Таким образом, первоначальная КНФ| сводится к более простой форме:
. Значит, единичный член конъюнкции можно просто опустить. Таким образом, первоначальная КНФ| сводится к более простой форме:  .
. (симметрия нарушена по переменной
(симметрия нарушена по переменной  . В левой части стоит ранее полученная КНФ. Значит, эту КНФ действительно можно свести к более простой форме.
. В левой части стоит ранее полученная КНФ. Значит, эту КНФ действительно можно свести к более простой форме. .
.

 . В этой формуле симметрия нарушена только по одной переменной
. В этой формуле симметрия нарушена только по одной переменной  и произведем группировку:
и произведем группировку:



