
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аудиторная контрольная работа №1Содержание книги
Поиск на нашем сайте Примечание 1: номер варианта контрольной работы выбирается в соответствии с порядковым номером (последней цифрой номера) студента в списке группы. Примечание 2: максимальное количество баллов за каждое из заданий контрольной работы приведено в варианте №1. Варианты заданий Вариант №1 Задание 1. Укажите единичные и общие понятия. Определите, какие общие понятия являются регистрирующими, а какие - нерегистрирующими; выделите собирательные понятия. 1) источник права, 2) Организация Объединенных Наций, 3) юридическое лицо, 4) коллектив, 5) каталог, 6) участник обороны Севастополя, 7)государственный бюджет РФ, 8) крейсер «Варяг», 9) декабрист, 10) частное от деления на нуль. (максимальное количество баллов - 10) Задание 2. Установите, в каком смысле собирательном или разделительном — употребляются выделенные понятия. 1) Сочинения Ф. М. Достоевского отличаются глубоким психологизмом. 2) Сочинения Ф. М. Достоевского составляют несколько томов.3) Закон пришел на смену правовому обычаю. (максимальное количество баллов - 3) Задание 3.Дайте полную логическую характеристику понятиям. 1) правительство,2) западная граница государства,3) невиновность. 4) учитель, 5) законность, 6) приговор, 7) бескорыстие, 8) отечество, 9) министерство юстиции, 10)мужество космонавта Леонова. (максимальное количество баллов - 10) Задание 4.Приведите по три примера понятий, находящихся в отношении: а) равнообъемности; б) противоположности; в) соподчинения. (максимальное количество баллов - 9) Задание 5.Выполните операции обобщения и ограничения понятий. 1) преступление, 2) повесть, 3) дезертирство. (максимальное количество баллов - 6) Задание 6.Определите, в каком отношении находятся приведенные понятия и изобразите отношения между понятиями при помощи круговых диаграмм (кругов Эйлера) 1) школьник, студент, учащийся, 2) мать, дочь, женщина, внучка, 3) мысль, понятие, суждени, 4) простое предложение, сложное предложение, предложение, придаточное предложение, 5) книга, словарь, энциклопедия, 6) студент, сдавший все экзамены на «отлично», студент, сдавший, по крайней мере, один экзамен «на отлично», студент, сдавший, по крайней мере, один экзамен на «хорошо», 7) писатель, русский писатель, Максим Горький, 8) республика, монархия, форма правления, президентская республика, парламентарная республика, 9) год, месяц, 10) холод, жара. (максимальное количество баллов - 10) Задание 7.Установите правильность определения понятий (в неправильных определениях укажите, какое правило нарушено). 1) Гипербола — стилистическая фигура, основанная на учете интенсивности признаков предмета. 2) Параллелограммом называется четырехугольник, две противоположные стороны которого параллельны. (максимальное количество баллов - 2) Задание 8.Установите правильность деления понятий (в случае неправильного деления укажите, какое правило нарушено). 1) Дети делятся на две категории — на невоспитанных и наших. 2) Видами развития являются развитие в неорганической природе, развитие в органической природе, развитие в обществе, развитие в познании. Задание 9.Постройте классификацию следующих понятий: 1) книга, 2) преступление. (максимальное количество баллов - 2) Задание 10. 1) Произведите операции умножения (пересечения) сложения (объединения) классов, использовав понятия задания 6. Операции запишите при помощи знака «*» («+») и изобразите в виде схем. (максимальное количество баллов - 20) 2) Образуйте дополнение к классу: а) земля, планеты Солнечной системы; б) летательные аппараты, дельтапланы. (максимальное количество баллов - 2) Примечание: минимально необходимое количество баллов – 40
Вариант №2 Задание 1. Укажите положительные и отрицательные понятия.
Задание 2. Установите, в каком смысле собирательном или разделительном — употребляются выделенные понятия. 1) Человек осваивает космос. 2) Человек имеет право на гражданство. 3) Крупные ученые всегда были в известной мере поэтами (Паустовский). Задание 3.Дайте полную логическую характеристику понятиям. 1) молодежный фольклорньий ансамбль, 2) Южный полюс, 3) небрежность, 4) газета «Труд», 5) качество, 6) несовместимость, 7)невежливость, 8)неорганическое вещество, 9) отсутствие должной предусмотрительности, 10) общее понятие.
Задание 5.Выполните операции обобщения и ограничения понятий. 1) общественное порицание, 2) бухгалтер, 3) право. Задание 6. Определите, в каком отношении находятся приведенные понятия и изобразите отношения между понятиями при помощи круговых диаграмм (кругов Эйлера) 1) гуманный, негуманный, 2) глава государства, президент, монарх, 3) крестьянское поселение, село, 4) юрист, прокурор, адвокат, 5) каменный дом, трехэтажный дом, одноэтажный дом, недостроенный дом, 6) героизм, трусость 7) уважение к старшему, неуважение к старшему, 8) пожар, молния, стихийное бедствие, явление природы 9) педагогический институт, биологический факультет, 10) экономический факультет ТГТУ, юридический факультет ТГТУ. Задание 7.Установите правильность определения понятий (в неправильных определениях укажите, какое правило нарушено). 1) Параллельные линии это прямые линии, которые не пересекаются ни при каком продолжении их в обе стороны. 2) Логика — это наука о правильных рассуждениях; известно, что правильные рассуждения — это рассуждения, подчиняющиеся законам логики. Задание 8.Установите правильность деления понятий (в случае неправильного деления укажите, какое правило нарушено). 1) Феодальная монархия делится на раннефеодальную монархию, монархию периода феодальной раздробленности, сословную монархию и абсолютную монархию. 2) Договоры делятся на устные, письменные и безвозмездные. Задание 9.Постройте классификацию из перечисленных понятий: Эпическое произведение, лирическое стихотворение, комедия, роман, трагедия, литературное произведение, эпическая поэма, лирическое произведение, песня, драма, рассказ, лирическая поэма, эпопея, театральное произведение, повесть. Задание 10. 1) Произведите операции умножения (пересечения) сложения (объединения) классов, использовав понятия задания 6. Операции запишите при помощи знака «*» («+») и изобразите в виде схем. 2) Образуйте дополнение к классу: 1) источники знания, художественные произведения; правовые науки, уголовное право. Вариант №3 Задание 1. Определите, являются ли данные понятия безотносительными или соотносительными. 1) народный суд, 2) начало, 3) причина, 4)рабочий, 5) север, 6) политика, 7) истец, 8) у сыновитель, 9) копия, 10) наука. Задание 2. Установите, в каком смысле собирательном или разделительном — употребляются выделенные понятия. 1)Полноводны и могучи реки Сибири. 2) В странах Азии проживает более половины всего человечества. 3) Книга — лучший подарок. Задание 3.Дайте полную логическую характеристику понятиям. 1) самая удаленная точка Вселенной, 2) значимая часть слова («морфема»), 3) человек, который никого не любит, 4) записка или письмо с просьбой куда-нибудь явиться, 5) призрак умершего или отсутствующего существа, 6) человек, у которого отсутствует воля, 7)человек, не знающий страха, 8)бестелесная простая единица бытия, являющаяся неделимой, неуничтожимой, неповторимой, психически активной и т.д. («Монада Лейбница»), 9) разумное существо, живущее на Марсе, 10) единичное понятие. Задание 4.Приведите по три примера понятий, находящихся в отношении: а) равнообъемности; б) соподчинения; в) подчинения. Задание 5.Выполните операции обобщения и ограничения понятий. 1) революция, 2) форма мышления, 3) периодическое издание. Задание 6.Определите, в каком отношении находятся приведенные понятия и изобразите отношения между понятиями при помощи круговых диаграмм (кругов Эйлера) 1) разбой, преступление против собственности, грабеж 2) университет, высшее учебное заведение, академия, 3) земледелец, пахарь, 4) изобразительное искусство, живопись, графика, скульптура, 5) артиллерист, сержант 6) свободный, несвободный 7) организатор,пособник,соучастник преступления, 8) халатность, взятка, 9) пролог, эпилог, 10) такса, сеттер, русская псовая борзая. Задание 7.Установите правильность определения понятий (в неправильных определениях укажите, какое правило нарушено). 1) Общество есть дополненная или расширенная личность, а личность — сжатое, или сосредоточенное общество (Владимир Соловьев). 2) Покой — это отсутствие беспокойства. Задание 8.Установите правильность деления понятий (в случае неправильного деления укажите, какое правило нарушено). 1) В России конца ХVIII века имелись следующие сословия: духовенство, дворянство и буржуазия. 2) Государства делятся на монархические, республиканские и демократические. Задание 9.Постройте классификацию из перечисленных понятий: Параллелограмм, непрямоугольный ромб, четырехугольник, непараллелограмм, непрямоугольный неравносторонний параллелограмм, прямоугольник, квадрат, непрямоугольный параллелограмм, неравносторонний прямоугольник, трапеция с двумя непараллельными сторонами, не-трапеция. Задание 10. 1) Произведите операции умножения (пересечения) сложения (объединения) классов, использовав понятия задания 6. Операции запишите при помощи знака «*» («+») и изобразите в виде схем. 2) Образуйте дополнение к классу: 1) завещатель, дееспособный завещатель; рецидивисты, преступники. Вариант №4 Задание 1. Определите, являются ли данные понятия безотносительными или соотносительными. 1) преемник, 2) проблема, 3) ведущий, 4) взяткодатель,5) наставник, 6) право, 7) племянник,8) практика, 9) оригинал, 10) врач. Задание 2. Установите, в каком смысле собирательном или разделительном — употребляются выделенные понятия. 1) Развивающиеся страны, где проживает более двух миллиардов человек, являются регионом бедности. 2) Ничто не возвышает человека больше, чем знания. 3) Мыслящий и работающий человек есть мера всему. (Вернадский). Задание 3.Дайте полную логическую характеристику понятиям. 1) письменное приглашение, 2) привидение, 3) безвольный человек, 4) отсутствие страха перед опасностью, 5) человек, который ничего не знал, 6) преступление, 7)необезвреженные сточные воды, 8)моя третья первая любовь, 9) человек, который ничего не знал о данном факте, но написал о нем другому, 10) конкретное понятие. Задание 4.Приведите по три примера понятий, находящихся в отношении: а) равнообъемности; б) противоречия; в) пересечения. Задание 5.Выполните операции обобщения и ограничения понятий. 1) закон, 2) наказание, 3) республика. Задание 6.Определите, в каком отношении находятся приведенные понятия и изобразите отношения между понятиями при помощи круговых диаграмм (кругов Эйлера) 1) университет, высшее учебное заведение, академия, 2) автор романа «Война и мир», русский писатель, писатель, мыслитель 3) верующий, православный, католик, 4) противоречие, конфликт, 5) глубокий, мелкий, 6) сын, отец, 7) еженедельник, периодическое издание, 8) кража, мошенничество, 9) четное число, число, кратное 5, 10) хищное животное, животное семейства кошачьих. Задание 7.Установите правильность определения понятий (в неправильных определениях укажите, какое правило нарушено). 1) Бразилия — страна неожиданностей. 2) Ёж — это существо, колючее на ощупь. Задание 8.Установите правильность деления понятий (в случае неправильного деления укажите, какое правило нарушено). 1) Животные делятся на хищников, травоядных, всеядных и млекопитающих. 2) Республики бывают рабовладельческие, феодальные, президентские и парламентарные. Задание 9.Постройте классификацию из перечисленных понятий: Постройте классификацию треугольников, применяя следующие основные деления: 1) величина наибольшего угла в треугольнике; 2) наличие хотя бы двух равных сторон; 3) наличие трех равных сторон. Задание 10. 1) Произведите операции умножения (пересечения) сложения (объединения) классов, использовав понятия задания 6. Операции запишите при помощи знака «*» («+») и изобразите в виде схем. 2) Образуйте дополнение к классу: 1) республика, форма правления; 2) иррациональное число, действительное число.
Задание 1. Укажите единичные и общие понятия. Определите, какие общие понятия являются регистрирующими, а какие - нерегистрирующими; выделите собирательные понятия 1) Московский государственный университет, 2) высшее учебное заведение, 3) свод законов, 4) правовая норма, 5) Российская Федерация, 6) преступное деяние, 7) депутат, 8) бригада морской пехоты, 9) рабочий класс,10) самое большое натуральное число. Задание 2. Установите, в каком смысле собирательном или разделительном — употребляются выделенные понятия. 1) Судьи и присяжные заседатели независимы и подчиняются только закону. 2) Все функции государства органически взаимодействуют между собой. 3) Студенты, получившие оценки «хорошо» и «отлично» во время экзаменационной сессии, получают стипендию. Задание 3. Дайте полную логическую характеристику понятиям. 1) университет, 2) преступность, 3) треугольник, 4) бесконечность, 5) человек, который ничего не знал, 6) вечный двигатель, 7)молчание, 8)тьма, 9) отцовство, 10) человек, который застрелился, нанеся себе три раны, каждая из которых вызвала немедленную смерть. Задание 4.Приведите по три примера понятий, находящихся в отношении: а) противоречия; б) противоположности; в) подчинения. Задание 5.Выполните операции обобщения и ограничения понятий. 1) плоская геометрическая фигура, 2) учебная дисциплина, 3) акция. Задание 6.Определите, в каком отношении находятся приведенные понятия и изобразите отношения между понятиями при помощи круговых диаграмм (кругов Эйлера) 1) государство, федеративное государство, унитарное государство, 2) ученый, юрист, общественный деятель, 3) участник Великой Отечественной войны, полковник, генерал, 4) судебное решение, приговор, судебное определение, 5) грамотный, не умеющий читать человек, 6) наказание, лишение свободы на определенный срок, исправительные работы, 7) эрудиция, невежество, 8) действие, бездействие, 9) четное число, рациональное число, 10) хищное животное, теплокровное животное. Задание 7.Установите правильность определения понятий (в неправильных определениях укажите, какое правило нарушено). 1) Человек - животное, способное к совершению купли и продажи» (Аль-Фараби). 2) Ночное время — это время с 22 до 6 часов по местному времени. Задание 8.Установите правильность деления понятий (в случае неправильного деления укажите, какое правило нарушено). 1) Параллелограммы делятся на прямоугольники, ромбы и непрямоугольные неравносторонние параллелограммы. 2) Люди делятся на мужчин, женщин и детей. Задание 9.Постройте классификацию изучаемых Вами учебных дисциплин, самостоятельно определив на каждом уровне классификации основания деления. Задание 10. 1) Произведите операции умножения (пересечения) сложения (объединения) классов, использовав понятия задания 6. Операции запишите при помощи знака «*» («+») и изобразите в виде схем. 2) Образуйте дополнение к классу: 1) студенты экономического факультета, студенты ТГТУ; 2) живописец, художник. 3. СОДЕРЖАНИЕ И БАЛЛЬНЫЕ ОЦЕНКИ АУДИТОРНЫХ И ВНЕАУДТОРНЫХ САМОСТОЯТЕЛЬНЫХ И КОНТРОЛЬНЫХ РАБОТ (9-18 УЧЕБНЫЕ НЕДЕЛИ)
Тема 4 Информационный материал Суждение - это мысль, в которой утверждается наличие или отсутствие каких-либоположений дел. В языке суждение, как правило, выражается повествовательным предложением иможет оцениваться в качестве истинного или ложного. Простым называется суждение, в котором нельзя выделить часть, в свою очередь являющуюся суждением. Основными видами простых суждений являются атрибутивные суждения, суждения об отношениях и суждения существования (экзистенциальные суждения). Атрибутивные суждения. Атрибутивными называются суждения, в которых выражается принадлежность предметам свойств или отсутствие у предметов каких-либо свойств. Атрибутивные суждения можно истолковать как суждения о полном или частичном включении или невключении одного множества предметов в другое или как суждения о принадлежности или непринадлежности предмета классу предметов. В каждом атрибутивном суждении есть субъект (логическое подлежащее), предикат (логическое сказуемое) и связка (связка иногда лишь подразумевается), а в некоторых имеются еще так называемые кванторные (количественные) слова («некоторые», «все», «ни один» и др.). Субъект и предикат называются терминами суждения. Субъект часто обозначается латинской буквой S (от слова «subjectum») а предикат - Р(от слова «ргаеdiсаtum»). В суждении «Некоторые науки не являются гуманитарными субъект (S) «науки», предикат (Р ) - «гуманитарные», связка не являются», а «некоторые» - кванторное слово. При решении вопроса о правильности и неправильности рассуждений и в некоторых других случаях используется так называемое объединенное деление атрибутивных суждений по качеству и количеству на общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные. Их структура и обозначения, соответственно: «Все S суть P» (А), «Ни одно S не суть Р» (Е), «Некоторые S суть Р» (I), «Некоторые Sне суть P»(О). Субъект и предикат суждения могут быть распределены (взяты в полном объеме) или не распределены (взяты не в полном объеме). В общих суждениях распределены субъекты, а в отрицательных - предикаты. Термин распределен, если для решения вопроса об истинности суждения следует исследовать все элементы объема термина. Если распределенный термин отметить знаком «+», а не распределенный – знаком «-», то получаем: все S+ суть Р-; ни один S+ не суть Р+; некоторые S- суть Р-; некоторые S- не суть Р+. Суждения об отношениях. Суждение, в котором говорится о том, что определенное отношение имеет место (или не имеет места) между элементами пар, троек и т.д. предметов, называется суждением об отношениях. Суждения об отношениях делятся по качеству на утвердительные и отрицательные, так же, как и аьтрибутивные. Суждения об отношениях делятся на виды и по количеству. Так, суждения об отношениях делятся по количеству на единично-единичные, обще-общие, частно-частные, единично-общие, единично-частные, обще-единичные, частно-единичные, обще-частные и частно-общие. Например: «Иванов выше Петрова» (единично-единичные), «Каждый студент нашей группы знает каждого преподавателя нашего факультета» (обще-общее), «Иванов знает каждого студента первого курса экономического факультета» (единично-общее). Аналогично деление на виды по количеству суждений выполняется для трехместных, четырехместных и т. д. отношениях. Основными видами отношений между суждениями по логическим формам являются отношения: совместимости по истинности, совместимости по ложности и логического следования. Производными от них - отношения логической эквивалентности, подчинения, контрадикторности, контрарности, субконтрарности и логической независимости. Отношение логической совместимости по истинности имеет место между сужениями А и В, если и только если логические формы этих суждений таковы, что существуют суждения А’ и В’ этих логических форм (но, возможно, других нелогических содержаний), такие, что оба они являются истинными. Если такие суждения А’ и В’ не существуют, то между исходными суждениями имеет место отношение логической несовместимости по истинности. Очевидно, что в этом отношении могут находится два и более суждений. Отношение логической совместимости по ложности имеет место между сужениями А и В, если и только если логические формы этих суждений таковы, что существуют суждения А’ и В’ этих логических форм (но, возможно, отличающиеся от исходных суждений своими нелогическими содержаниями), такие, что оба они являются ложными. Если такие суждения А’ и В’ не существуют, то между исходными суждениями А и В имеет место отношение логической несовместимости по ложности. Отношение логического следования имеет место между сужениями А и В, если и только если не существуют суждения А’ и В’ этих логических форм (но, возможно, других нелогических содержаний), такие, что А’ истинно, а В’ – ложно (обозначается А╞ В). Отношение логического следования имеет место между множеством суждений {А1, А2, …Аn} и суждение В (обозначается А1, А2, …Аn╞ В), если и только если не существуют суждения А’1, А’2, …А’n, В’ тех же логических форм (но, возможно, других нелогических содержаний), такие, что А’1, А’2, …А’n истинны, а В’ – ложно. Отношение логической эквивалентности имеет место между суждениями А и В, если и только если А╞ В и В╞ А. Оно обозначается следующим образом: А↔В. Суждения А и В находятся в отношении подчинения, если и только если А╞ В и неверно, что В╞ А. Суждение А называется в этом случае подчиняющим, а суждение В - подчиненным. Отношение контрадикторности (противоречия) имеет место между суждениями, которые несовместимы по истинности и несовместимы по ложности. Контрарными (противоположными) называются суждения, которые совместимы по ложности, но несовместимы по истинности. Субконтрарными (частично совместимыми) называются суждения, которые совместимы по истинности, но несовместимы по ложности. Суждения называются логически независимыми, если и только если все они совместимы по истинности и ложности и каждое из них не находится в отношении логического следования к другим из рассматриваемой совокупности суждений. Отношения между атрибутивными суждениями с одними и теми же терминами изображаются с помощью мнемонической схемы, называемой логическим квадратом.
Аудиторная самостоятельная работа №8 «Простые суждения. Объединенная классификация простых суждений. Распределенность терминов в суждении. Отношения между суждениями» Задание №1. Укажите, какие из приведенных высказываний являются общеутвердительными, общеотрицательными, частноутвердительными, частноотрицательными: (максимальное количество баллов - 13) а) Всякий моряк умеет плавать. б) У каждой лошади есть хвост. в) Ни одна кошка не дружит с мышами. г) Есть кошки, которые дружат с собаками. д) Не все книги содержат полезную информацию. е) Привидения не существуют. ж) Некоторые люди не умеют писать. з) На всякого мудреца довольно простоты. и) Не все то золото, что блестит. к) Ряд водоплавающих не дышит жабрами. л) Несколько человек не пошли в музей. м) Многие люди все еще верят в злых духов. н) Люди в подавляющем своем большинстве хотят добра. Задание №2. Определить вид суждения, его субъект и предикат, их распределенность изобразить схематически при помощи круговых диаграмм. (максимальное количество баллов - 10) а) Некоторые растения не являются лекарственными. б) Ни одно нераспространенное предложение не является предложением, имеющим второстепенные члены. в) Иногда люди допускают несправедливость. г) Всякий металл имеет свою температуру плавления. д) Некоторые олимпийские чемпионы являются мастерами спорта по фигурному катанию. е) Все ромбы - четырехугольники. ж) Ни один океан не имеет пресную воду. з) Под лежачий камень вода не течет. и) Некоторые сотрудники являются необязательными людьми. к) Хорошее дело два века живет.
Задание №3. Какие из следующих высказываний противоречат друг другу: а) Каждый кашалот является водоплавающим. б) Ни один кашалот не является водоплавающим. в) Отдельные кашалоты не являются водоплавающими. г) Некоторые кашалоты — водоплавающие. д) Не все кашалоты дышат жабрами. е) Нет кашалота, который дышал бы жабрами. ж) Кашалот дышит жабрами. з) Некоторые кашалоты дышат жабрами. (максимальное количество баллов - 2) Задание №4. Какие из приведенных высказываний не могут быть вместе истинными, но могут быть вместе ложными: а) Все лыжники — мастера спорта. б) Некоторые лыжники не являются мастерами спорта. в) Ни один лыжник не является мастером спорта. г) Отдельные лыжники — мастера спорта. (1 балл) Задание №5. Какие из приведенных высказываний могут быть одновременно истинными, но не могут быть одновременно ложными: а) Все врачи окулисты. б) Некоторые из врачей окулисты. в) Некоторые врачи не окулисты. г) Среди врачей нет окулистов. (1 балл) Задание №6. Какие из приведенных высказываний находятся в отношении логического следования: а) Некоторые люди являются художниками. б) Некоторые люди не относятся к художникам. в) Ни один человек не является художником. г) Каждый человек — художник. (максимальное количество баллов - 2)
Указание: при выполнении упражнений 3 – 6 удобно пользоваться схемой «логический квадрат». Домашняя самостоятельная работа №4 Задание: подготовка краткого конспекта теоретического вопроса «Модальные суждения». Требования к оформлению: не более 2 печатных листов (14 кегль, 1,5 интервал), указание на используемую литературу и интернет - ресурсы.
Примечание: максимальная оценка - 5 баллов, необходимо набрать не менее 3 баллов. Тема 4 (продолжение) Информационный материал Сложные суждения образуются из простых, а так же из других ложных суждений помощью логических союзов «если … то….», «или», «и» и т. д., с поощью отрицания «неверно, что…», модальных терминов «возможно, что..», «необходимо, что…», «случайно, что…», и т. д. Соединительные суждения – это суждения, в которых утверждается наличие двух и более ситуаций. Чаще всего такие суждения выражаются посредством предложений, содержащих союз «и». Встречающийся в естественном языке союз «и» употребляется в нескольких значениях. В логике употребляется союз «и», имеющий определенный смысл. Этот союз обозначается символом Форма конъюнктивного суждения: (
Разделительные суждения – это суждения, в которых утверждается наличие одной из двух, трех и более ситуаций. Если утверждается наличие по крайней мере одной из двух ситуаций, суждение называется нестрого разделительным, или дизъюнктивным. Если утверждается наличие ровно одной из двух или более ситуаций, то суждение называется строго-разделительным или строго-дизъюнктивным. Чаще всего утверждения первого типа реализуются посредством предложений с союзом «или, «либо», а второго - с союзом «или, …или», «либо,.. либо». Союз «или», посредством которого выражается утверждение первого типа, обозначается символом Табличные определения знаков нестрогой и строгой дизъюнкции имеют вид:
Примерами нестрого- и строго-дизъюнктивного суждения могут служить следующие сложные суждения: «Иванов является юристом или Иванов является спортсменом», «Либо Иванов совершил это преступление, либо Иванов не совершал этого преступления». Символ
Пример суждения этого вида: «Или Иванов совершил это преступление, или Петров, или Сидоров». Условные или импликативные суждения. Суждения, в которых утверждается, что наличие одной ситуации обуславливает наличие другой, называется условным. Условные суждения чаще всего выражаются предложениями союзом «если.., то …». В условном суждении выделяют основание и следствие. Основанием (антецендентом) называется та часть условного суждения, которая располагается между словом «если» и словом «то». Часть условного суждения, которая находится после слова «то», называется следствием (консеквентом). Условный союз «если…, то …» обозначается знаком «→». В построениях современной логики находит широкое распространение союз «если.., то …», обозначаемый символом «
Суждения эквивалентности и материальной эквивалентности. Суждения эквивалентности – это суждения, в которых утверждается взаимная обусловленность двух ситуаций. Суждения эквивалентности выражаются, как правило, посредством предложений с союзами «если и только если, то…», «тогда п и только тогда, когда…», «необходимо и достаточно». Союз «если и только если, то…», употребляемый в описанном смысле, обозначается символом «↔». Союз «если и только если, то…» употребляется еще в одном смысле. В этом случае он обозначается символом «
Суждения с этим союзом называются суждениями материальной эквивалентности. Суждения с внешним отрицанием – это суждения, в которых утверждается отсутствие некоторой ситуации. Оно чаще всего выражается предложением, начинающимся словосочетанием «неверно, что». Внешнее отрицание обозначается знаками «», «
Аудиторная самостоятельная работа №9 «Сложные суждения. Построение таблиц истинности сложных суждений» Задание №1. Определите значения истинности следующих высказываний: а) Луна—планета и 2+3=5. б) Луна—планета или 2+3=5. в) 1—простое число и 2—простое число. г) 1 — простое число или 2 — простое число. д) Кислород—металл и 2Х2 ==5. е) Кислород—металл или 2Х2 =5. ж) Цинк — металл и цезий — металл. | з) Цинк — металл или цезий — металл. (максимальное количество баллов - 8) Задание №2. Определите значения истинности высказываний а, b, с, d если: а) а & (Марс—планета)—истинное высказывание; б) b & (Марс—планета)—ложное высказывание; в) с или (Солнце—спутник Земли)—истинное высказывание; г) d & (Солнце—спутник Земли)—ложное высказывание. (максимальное количество баллов - 4) Задание №3. Укажите значения истинности следующих высказываний: а) Данное число четно или число, большее его на единицу, четно. б) Данное число четно и число, большее его на единицу четно. в) Две прямые на плоскости параллельны или пересекаются. г) Две прямые на плоскости параллельны и пересекаются. (максимальное количество баллов - 4) Задание №4. Укажите значения истинности приведенных высказываний: а) Каждое число делится на 2 или делится на 3. б) Произвольно взятое число либо делится на 2, либо делится,на 3. в) Эйфелева башня находится в Париже или она находится в Нью-Йорке. г) Либо Эйфелева башня находитсяв Париже, либо она в Нью-Йорке. д) Лев Толстой написал роман «Воскресение» или он написал роман «Анна Каренина». е) Либо Лев Толстой написал «Воскресение», либо он написал «Анну Каренину». (максимальное количество баллов - 5) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |



 (читается «и»), называемый знаком конъюнкции. Суждение с этим союзом называется конъюнктивным. Определением знака конъюнкции является таблица показывающая зависимость истинности конъюнктивного суждения от истинности составляющих его суждений.
(читается «и»), называемый знаком конъюнкции. Суждение с этим союзом называется конъюнктивным. Определением знака конъюнкции является таблица показывающая зависимость истинности конъюнктивного суждения от истинности составляющих его суждений. ). Каждое из высказываний А и В может принимать как значение «истина», так и значение «ложь». Эти значения для краткости будем обозначать «и», «л» («1» или «0»). Таблица истинности для соединительного суждения имеет вид:
). Каждое из высказываний А и В может принимать как значение «истина», так и значение «ложь». Эти значения для краткости будем обозначать «и», «л» («1» или «0»). Таблица истинности для соединительного суждения имеет вид: (читается «или»), называемым знаком нестрогой дизъюнкции (или просто знаком дизъюнкции), а союз «или, … или», посредством которого выражается утверждение второго типа, - символом
(читается «или»), называемым знаком нестрогой дизъюнкции (или просто знаком дизъюнкции), а союз «или, … или», посредством которого выражается утверждение второго типа, - символом  (читается «или, … или»), называемым знаком нестрогой дизъюнкции.
(читается «или, … или»), называемым знаком нестрогой дизъюнкции.

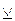 (в другой терминологии
(в другой терминологии  ». Этот символ называется знаком (материальной) импликации, а суждение с этим союзом - импликативным. Знак импликации определяется следующей таблицей истинности:
». Этот символ называется знаком (материальной) импликации, а суждение с этим союзом - импликативным. Знак импликации определяется следующей таблицей истинности:
 », называемым знаком материальной эквивалентности, который определяется следующей таблицей истинности:
», называемым знаком материальной эквивалентности, который определяется следующей таблицей истинности:
 », «
», « », называемыми знаками внешнего отрицания. Этот знак определяется следующей таблицей истинности:
», называемыми знаками внешнего отрицания. Этот знак определяется следующей таблицей истинности:


