Тема I . Предмет и задачи логики.

 

Мышление как предмет изучения логики. Ступени процесса познания: чувственное познание и абстрактное мышление. Особенности абстрактного мышления, 3 его основные формы: понятие, суждение, умозаключение. Роль языка в познании.

 

Логика как наука о законах и формах правильного мышления. Понятие логической формы. Конкретное содержание и логическая структура мысли. Понятие логического закона. Истинность мысли и правильность рассуждений по форме. Основные черты правильного рассуждения: определенность, непротиворечивость, последовательность и доказательность.

При изучении этой темы следует обратить внимание на то, что выделению логики как особой ветви знания способствовали два обстоятельства:

1) еще в древности люди знали, что достоверность выводных знаний зависит не только от истинности исходных посылок, но и от способа их соединения;

2) чтобы убеждать, надо не только хорошо говорить, но и владеть различными приемами построения умозаключений и доказательств.

Поэтому логика использовалась теоретически и практически в повседневной интеллектуально – речевой деятельности и вошла в программу европейских университетов в составе так называемого тривиума – первой ступени высшего образования, куда, кроме логики, входили грамматика и риторика.

Особый акцент в теме I должен быть сделан на формирование совокупности умений такого рода, которые называются логической культурой личности и которые определяются врожденным потенциалом индивида, окружающей социальной средой и определенной логосферой.

Для решения поставленных в теме I задач следует овладеть такими узловыми понятиями, как логика, наука, закон и форма мышления, чувственное и рациональное познание и воспользоваться рекомендованной учебной и методической литературой: стр. 3 – 10, 13 – 19.

 

Вопросы для самопроверки и повторения темы I.

 

1. Что изучает логика?

2. Что представляет собой чувственное познание и каковы его основные формы?

3. Что такое абстрактное мышление, какова его роль в познании.

4. Что такое логическая культура личности?

5. Почему необходимо изучать логику?

 

Тема II. Логика и язык

 

Язык как информационная знаковая система. Функции языка. Языки естественные и искусственные.

 

Понятие знака. Общая характеристика и виды знаков, предметное и смысловое значение языковых выражений. Основные семантические аспекты языка: синтаксис, семантика, прагматика.

 

Семантическая категория языка: дескриптивные и логические термины. Дескриптические (описательные) термины: имена предметов, выражения, обозначающие свойства и отношения, предложения. Логически термины: логические связки, кванторы.

Функциональный метод анализа языка. Понятие функций и функтора. Употребление переменных в логике, предметные, предикатные и пропозиционные переменные. Понятие пропозиционной (высказывательной) функции.

Искусственные языки науки логики. Понятие о языке логики высказываний. Понятие о языке логики предикатов.

Основная цель при осмыслении темы II – освоение языка логики предикатов, которая отражает и следует за смысловыми характеристиками естественного языка. Для этого рекомендуется алфавит языка логики предикатов оформить в виде следующей таблицы

 

Символ	Способ употребления	Название	Как читается
	·	p q	Конъюнкция	p и q
v		pvq	Дизъюнкция слабая или не исключающая	p или q
v		p v q	Дизъюнкция сильная или исключающая	либо p, либо q
		p q	Импликация	если p, то q
		p q	Эквиваленция, тождество	p тогда и только тогда, когда q
		p	Отрицание	не верно, что p
		p	Необходимость	необходимо, что р
		p	Возможность	возможно, что р
		(x) p(x)	Квантор общности	для всякого х верно, что р – х
		(x) p(x)	Квантор существования	существует такой х, что р - х
x, y, z			Символы для высказываний, предметные переменные
a, b, c			Символы для единичных предметов, предметные постоянные
p, q, r			Символы для высказываний, пропозициональные переменные
P, Q, R			Символы для предикатов, предикатные переменные

 

и в качестве узловых категорий данной темы выделить в собственных логических словариках следующие понятия: язык, знак, знак – образ, знак – символ, семиотика, синтаксис, семантика, прагматика, язык логики высказываний, язык логики предикатов, воспользовавшись указанной в списке литературой: [ 1 ], стр. 10 – 13.

 

Вопросы для повторения и самопроверки.

 

1. Что такое естественный язык?

2. Что такое искусственный язык?

3. Что представляет собой язык логики предикатов?

 

Тема III. Понятие

Понятие как форма мышления. Выражений понятий в языке. Основные логические приемы формирования понятий: анализ, синтез, абстрагирование, обобщение. Роль понятий в познании.

 

Логическая характеристика понятия. Содержание понятия. Признаки предметов и их виды, отличительные и не отличительные; необходимые и случайные; существенные и несущественные. Свойства и отношения как признаки.

Выражение содержания и объема понятий в языке логики предикатов. закон обратного отношения между объемом и содержанием понятий.

 

Виды понятий. Общие и единичные, относительные и безотносительные, собирательные и не собирательные понятия.

 

Отношения между понятиями. Сравнимые и несравнимые понятия. Виды сравнимых понятий: совместимые и несовместимые понятия. Типы совместимости: равнозначность, частичное совпадение (пересечение), подчинение. Типы несовместимости: соподчинение, противоположность, противоречие. Моделирование отношений между понятиями на кругах Э.Эйлера.

 

Операции обобщения и ограничения понятий. Деление понятий. Виды деления: по видоизменению признака и дихотомическое деление. Правила и ошибки в делении. Классификация естественная и искусственная. Значение деления и классификация в науке и практике.

 

Определение понятий. Номинальные и реальные определения, явные и неявные определения. Основной вид явных определений -– определение через род и видовое отличие (атрибутивные и генетические).

Приемы, сходные с определением: описание, характеристика, разъяснение посредством примера, сравнение, указание и др.

Правила определения. Ошибки, возможные в определениях. Значение определений в науке и практическом рассуждении. Требование диалектической логики к процессу определения научных понятий. Научная терминология.

при изучении данной темы необходимо уяснить, что понятие является универсальной единицей мышления и основой интеллектуальной деятельности. Важнейшими характеристиками понятия являются содержание и объем. Все логические характеристики и логические операции являются результатом выводных знаний из закона обратно пропорциональной зависимости между содержанием и объемом понятия. После осмысления и освоения основных определений по учебникам, методическим пособиям и логическим словарям рекомендуется закрепить информацию этого блока по следующей схеме:

 

1) по объему

 

2) по существованию

элементов

 

 

3) по структуре

элементов

 

4) по содержанию

 

5) по наличию качеств,

св-в, отношений

 

6) по качеству

элементов

 

 

Абстрактные (белизна)

Конкретные (камень)

7) по характеру

объекта

 

 

Дать логическую характеристику любому понятию – это значит спроецировать его на приведенную схему и показать употребление понятия во всех 7 смыслах. Например, понятие должник является общим, непустым, собирательным, соотносительным, положительным, нерегистрируемым и конкретным.

После освоения логических операций с понятиями: ограничения, обобщения, определения и деления можно перейти к моделированию отношений между сравнимыми понятиями, которые лучше представить следующей схемой:

 

 

А

Равнооъем- Соподчинение:

А,В

ность: офицер-

С

В

Казань- майор-капитан

столица

РТ

 

А

В

Противополож-

ность (конт-

рарность):

белый-черный

 

Пересечение: пассажир-

студент

 

А

Противоречие

В

А

(конрадиктор-

ность):

В

белый-

небелый

 

Подчинение: дерево - береза

 

 

В заключении этой темы следует перейти к самопроверке и к ответу на 7 условных вопросов:

1) Что понимается под содержанием и объемом понятия, каково между ними отношение?

2) Какие виды понятий Вам известны?

3) Что значит «определить» понятие?

4) Каковы правила определений?

5) Какая логическая операция называется делением понятия?

6) Каковы правила и ошибки деления?

7) Что такое обобщение и ограничение понятий?

воспользовавшись указанной в начале литературой:

[ 1 ] стр.46 – 62

[ 4 ] стр. 4 – 46

[ 5 ] стр. 3 – 20

 

Для закрепления освоенного материала можно рекомендовать следующие упражнения:

I. Дать логическую характеристику понятиям:

1) Государство; 2) Актер; 3) Равенство (партнерство); 4) Здание;

5) Сделка; 6) Парламент; 7) Консенсус.

II. Установить вид и правильность определений:

1) Абитуриент – учащийся, окончивший школу и сдавший вступительные экзамены в вуз.

2) Барометр – прибор для измерения давления, в котором запаянную сверху стеклянную трубку опускают открытым концом в ртуть.

3) Рецензия – литературная работа, для создания которой нужно проанализировать какое – либо художественное произведение и сопроводить его критической оценкой.

4) Русские – это славяне, которые не украинцы и не белорусы.

5) Умный человек – это тот, который молчит, когда его не спрашивают.

 

III. Определить правильность обобщения и ограничения понятий:

1) Европейское государство – Франция – город на Сене – Париж.

2) Университет –гуманитарный факультет – исторический факультет.

3) Столица – Москва – центр Москвы – Красная Площадь.

4) Карельская береза – береза – дерево – лес

5) Студент ТИСБИ – Иванов – человек – живое существо.

 

IV. Определить правильность деления понятий:

1) Транспорт: городской, воздушный, морской, велосипедный.

2) Очки: с диоптриями, без диоптрий.

3) Город: республиканского, областного и местного значения.

4) Время года: зима, весна, лето, осень.

5) Поезд: экспресс, курберский, скорый, пассажирский, местный.

 

V. Показать на кругах Эйлера отношения между понятиями:

1) Юрист, прокурор, адвокат, судья, защитник, преступник.

2) Российский студент, студент – юрист, студент ТИСБИ.

3) Русский писатель, дореволюционный писатель, советский писатель, Горький, Шолохов, Достоевский, Г. Баширов.

4) Отец; человек, имеющий двоих детей; человек, имеющий одного ребенка; человек, имеющий детей.

5) Акционерное общество; член АО; председатель правления АО; Петров.

Ключевые слова: содержание понятия, объем понятия, ограничение понятий, обобщение понятий, определение понятий, деление понятий.

 

Тема IV. Суждение

 

Суждение как форма мышления. Выражение суждений в языке. Повествовательные, побудительные, вопросительные предложения и их логический смысл. Простые и сложные суждения.

 

Простые суждения. Структура простого суждения. Виды простых суждений: атрибутивные, с отношениями, экзистенциальные. Категорические суждения и их виды (деление по количеству и качеству). Выделяющие и исключающие суждения. Распределенность терминов в категорических суждениях. Выражение категорических суждений в языке предикатов.

 

Отношения между суждениями по истинности. Отношения совместимости: эквивалентность, логическое подчинение, частичное совпадение (субконтрарность). Отношение несовместимости: противоречие (контрадиктарность). Логический квадрат. Табличный способ установления отношений между сложными высказываниями. Правила образования противоречащих суждений.

 

Сложные суждения. Образование сложных из простых с помощью логических связок: конъюнкции, дизъюнкции, импликации, эквивалентности и отрицания. Условия истинности сложных суждений. Строгая и нестрогая дизъюнкция. Импликация и условное суждение. Понятие необходимого и достаточного условий.

 

В любом познавательном процессе человек с помощью понятий устанавливает отношения между предметами и явлениями на истинность или ложность. Это отражается в мышлении в форме суждений, представляющих собой связь понятий.

При изучении данной темы необходимо обстоятельно разобраться в следующих вопросах, являющихся основанием для выводных знаний:

1. Суждение и предложение как языковая форма выражения суждения.

2. Простые суждения, их виды и структура.

3. Объединенная классификация суждений по количеству и качеству.

4. Распределенность терминов в суждениях.

5. Логический квадрат.

6. Логические отношения между суждениями.

7. Сложные суждения и табличный метод определения истинности сложных суждений.

Для этого рекомендуется воспользоваться указанной учебной и методической литературой и закрепить информацию с помощью следующих формализованных схем:

 

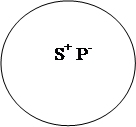
Состав суждения:

Субъект суждения: S – понятие о предмете суждения;

Предикат суждения: Р – понятие о признаке предмета;

Связка – утверждение или отрицание, мыслимое в предикате содержания.

 

S

 

Казань – столица РТ, «есть» – связка

 

Р

 

Формула суждения: «S есть Р»

 

Р

 

Петров не является студентом «S не есть Р»

 

S

 

 

 

 

Истинные юристы, как Казань восточнее Москвы Существуют вечнозе-

правило, скромны. леные деревья

 

Кроме трех представленных на схеме простых суждений, следует рассмотреть выделяющие и исключающие суждения и закрепить данный блок с помощью следующих упражнений:

I. Какие суждения могут быть выражены в следующих предложениях (найдите их субъекты и предикаты):

 

1. Нет студента, который не имел бы трудности при изучении логики.

2. Каждый может освоить этот курс самостоятельно.

3. Эта картина была подарена музею дочерью художника.

4. Цыплят по осени считают.

5. Никто в группе не был готов к семинару.

6. Иван Иванович – сосед Ивана Никифоровича.

7. Отчизне посвятим души прекрасные порывы.

8. Только некоторые люди, и только люди – врачи.

9. Все студенты 971 группы, за исключением Иванова, сдали зачет по логике.

 

В целях получения выводного знания и использования суждений в умозаключениях употребляется объединенная классификация суждений по количеству и качеству, и вводится понятие распределенности в них терминов- субъекта и предиката.

Объединенная классификация суждений:

1. Общеутвердительные суждения – А

«Все S суть Р» – Все поэты впечатлительные люди.

2. Общеотрицательные суждения – Е

«Ни одно S не есть Р» – Ни один человек не всеведущ.

3. Частноутвердительное суждение – I

«Некоторые S суть Р» - суть Р» - Некоторые люди имеют курчавые волосы.

4. Частноотрицательное суждение – О

«Некоторые S не есть Р» – Некоторые люди не умеют слушать.

 

Распределенность терминов в суждениях.

 

Термины	Виды суждений
А	Е	I	О
S	+	+	-	-
Р	-	+	-	+

 

Термин является распределенным, если его объем полностью входит в объем другого термина или полностью исключается из него, распределенность термина обозначается знаком «+». Термин является нераспределенным, если его объем составляет только часть объема другого термина, нераспределенность термина обозначается знаком «-». На кругах Эйлера это можно изобразить следующим образом:

 

S

I. А – Все рыбы позвоночные.

Р^-

S^+

Р

 

S

 

Все квадраты суть параллелограммы с равными сторонами и равными углами

 

Р

 

S

 

II. Е – ни одно насекомое не есть позвоночное.

 

Р

 

 

S

 

III. I – Некоторые книги полезны.

 

Р

Р^-

S^-

 

 

S

 

Не которые животные суть позвоночные.

	S^-

P^-

P

S

 

IV. – Некоторые книги не суть полезны.

Р

	Р^+		S ^-

 

 

 

S

 

Некоторые змеи не имеют ядовитых зубов.

	S^-

Р

 

 

Простые суждения, имеющие одинаковые термины и различающиеся по качеству и количеству, находятся в определенных отношениях по истинности и ложности, которые можно вывести с помощью схемы, называемой логическим квадратом.

 

 

Противоположность

А (контрарность) Е

п п

о о

д д

ч ч

и и

н н

е е

н н

и и

е е

I Частичная совместимость О

(субконтрарность)

 

Устанавливать типы отношений между суждениями по логическому квадрату важно при получении выводных знаний, сопоставлении разных точек зрения по дискуссионным вопросам, редактирования текстов и в других случаях.

После изучения данного блока учебного курса рекомендуется составить таблицу истинности и таблицу ложности суждений А, Е, О, I, обозначив истинность символом «1» и ложность символом «0». Эти таблицы не нужно знать наизусть, но должно уметь их выводить.

Если А 1, то Е 0, О 0, I 1;

Если Е 1, то О 1; I 0, А 0;

Если О 1, то I н, А 0; Е н;

Если I 1, то А н, Е 0; О н;

Если А 0, то Е н; О 1; I н;

Если Е 0, то О н; I 1; А н;

Если О 0; то I 1; А 1; Е 0;

Если I 0, то А 0; Е 1; О 1;

 

Для закрепления освоенного материала и в целях самопроверки вывести при помощи логического квадрата противоположные, противоречащие и подчиненные данным суждения, установив их истинность или ложность.

Пример:

Всякое суждение выражается в предложении. А 1

Ни одно суждение не выражается в предложении. Е 0

Некоторые суждения не выражаются в предложении. О 0

Некоторые суждения выражаются в предложении. I 1

 

1. Некоторые растения вредны.

2. Все науки осуществляются благодаря опыту.

3. Ни один лентяй не заслуживает похвалы.

4. Все студенты сдают экзамены.

5. Некоторые реки судоходны.

6. Никакое знание не бесполезно.

7. Некоторые звезды не видны.

 

В целях системного освоения и закрепления информации по теме “Суждение” рекомендуется базовые понятия записать в своей логический словарик, а рекомендуемые упражнения, схемы и таблицы записать в свой конспект.

После освоения предыдущий темы можно перейти к табличному методу определения истинности сложных суждений, состоящих из 2-х и более суждений. Для этого необходимо знать определения основных логических связок: конъюнкции, дизъюнкции (слабой и строгой), импликации, эквивалентности и отрицания (тема 3).чтобы построить таблицу истинности, нужно сначала, считая, что все простые суждения независимы друг от друга, перебрать все возможные сочетания их значений. Таких сочетаний будет – 2ⁿ, где n – число различных простых суждений в составе сложного суждения.

«В ТИСБИ имеются факультеты юридический, экономический и гуманитарный» – это сложное конъюнктивное суждение, состоящее из 3-х простых, его логическая форма (p ^q^r). Для этого случая в трех первых слева столбцах таблицы восемью строками (2³) записываются все сочетания значений пропозициональных переменных p, q, r. Механический перебор всех сочетаний осуществляется, если для первой переменной р записать половину строк (четыре строки) истиной (1) и половину ложной (0), для второй переменной чередовать «1» и «0» через две строки, а для последней r – через одну. После заполнения входных столбцов начинаем определять истинные значения сложного суждения, руководствуясь следующей таблицей:

 

p	q	p q	pvq	p v q	p q	p q	p

 

Тогда в нашем примере, кроме входных столбцов, появляется еще 2 столбца, где последний называется результирующим, т.е. дающим ответ на вопрос, при каких условиях истинно данное сложное суждение.

 

p	q	r	p q	q r

 

Для лучшего осмысления алгоритма выводов по таблице рекомендуется в конспекте сформулировать и записать истинность каждого вида связок и закрепить материал с помощью следующих упражнений:

Найдите составляющие сложное суждение простые суждения, определив тип связи и истинность сложных суждений с помощью таблиц истинности:

1. «Вам никогда не удается создать мудрецов, если будете убивать в детях шалунов» Ж.Руссо

2. «Кто утратил стыд, того нужно считать погибшим» Плавт

3. «Только та победа истинна, когда никто не считает себя побежденным» Будда

4. «Предварительное значение того, что собираешься сделать, дает смелость и легкость» Д. Дидро

5. «Мало иметь хороший ум, главное – хорошо его применять» Р. Декарт

6. «Поэтами рождаются, ораторами становятся» Цицерон

7. «Когда глаза говорят одно, а язык – другое, опытный человек больше верит первым» Эмерсон

 

Выполнение всех упражнений по теме «Суждение» является достаточным и необходимым условием для перехода к теме «Умозаключение», которая поможет получать новые знания – опосредованные или выводные.

Ключевые слова: суждения простые и сложные; логический квадрат; условия истинности простых и сложных суждений.

 

ТЕМА V. Умозаключение

 

Общее понятие о заключении. Структура умозаключения: посылки, заключение, логическая связь между посылками и заключением. Понятие логического следования. Виды умозаключения: дедуктивный, индуктивный, по аналогии. Логически необходимые и вероятные (правдоподобные) умозаключения.

 

Дедуктивные умозаключения. Понятие дедуктивного умозаключения. Необходимый характер логического следования в дедуктивных умозаключениях. Различные формы дедуктивных умозаключений.

 

Выводы из категорических суждений а) непосредственные умозаключения. Выводы посредством преобразования суждений: превращение, обращение, противопоставление предикату.

Выводы на основе истинностных отношений по логическому квадрату.

б) Категорический силлогизм. Состав силлогизма. Фигуры и модусы силлогизма. Правильные модусы. Общие правила силлогизма. Специальные правила фигур.

 

Индуктивные умозаключения. Понятие умозаключения. Связь индукции с опытными обобщения. Виды индуктивных умозаключений: полная и неполная индукция, популярная и научная индукция.

 

Статистические обобщения. Понятие о популяции, образце и частоте признака. Индуктивная природа статистических обобщений. Статистическая генерализация и статистический прогноз.

Роль индуктивных умозаключений в познании. Взаимосвязь индукции и дедукции в процессе познания.

 

Умозаключение по аналогии. Аналогия как умозаключение и его структура. Виды умозаключений по аналогии.

 

Роль выводов по аналогии в познания. Аналогия – логическая основа метода моделирования в науке и технике. Эвристическая и экспликативная функция выводов по аналогии в процессе познания и обучения.

 

При освоении данной темы следует уяснить, что речь идет о логической форме получения выводных знаний – умозаключений, посредством которой из двух и более суждений с необходимостью выводится новое суждение. Суждения, из которых выводится новое суждение называется посылками, новое суждение, полученное логическим путем из посылок, называется заключением. Дополнительную информацию по этой теме можно получить из источников, обозначенных в списке литературы. Существенным моментом, способствующим глубине усвоения учебного материала, является самостоятельный поиск ответов на контрольные вопросы, обозначенные в данном пособии и выполнение упражнений, предлагаемых в конце темы IV, особенно по логическому квадрату.

Далее следует уяснить, что в зависимости от числа посылок умозаключения делятся на: 1) непосредственные или умозаключения в несобственном смысле и 2) умозаключения в собственном смысле с тремя его видами: дедукция, индукция и традукция (аналогия).

В непосредственных умозаключениях (заключение выводится из одной посылки) уточнение знаний происходит через преобразование суждений: превращение,обращение,противопоставление предикату.

Превращением называется такое непосредственное умозаключение, в котором в выводе субъектом является субъект исходного суждения, а предикатом – понятие, противоречащее предикату исходного суждения, при этом связка изменяется на противоположную. Другими словами, это процесс изменения формы суждения, при этом смысл суждения не меняется.

 

Схема превращения суждений

(А) Все S суть Р ……………. (Е) Ни одно S не есть не – Р

(Е) Ни одно S не есть Р ……. (А) Все S суть не – Р

(О) Некоторые S не суть Р …. (I) Некоторые S суть не – Р

(I) Некоторые S суть Р ……. (О) Некоторые S не суть не – Р

 

Обращением называется такое непосредственное умозаключение, в котором в выводе субъектом является предикат, а предикатом – субъект исходного суждения, при этом связка остается неизменной.

Различают обращение с ограничением и простое, или чистое обращение. Если в исходном суждении предикат не распределен, то непосредственное умозаключение образуется путем обращения с ограничением, т.е. предикат исходного суждения становится субъектом выводного суждения с ограничением его объема. С ограничением обращается общеутвердительные суждения

P-

S

S+

(А) Все спортсмены – здоровые люди

P

S

P-

S-

Некоторые здоровые люди – спортсмены

 

Р

 

 

Без ограничения обращаются общеотрицательные (Е) и частноутвердительные (I) суждения, частноотрицательные (О) суждения не обращаются.

 

Схема обращения суждений

(А) Все S суть Р …………….. ………….(I) Некоторые Р суть S

(Е) Ни одно S не суть Р…….……………(Е) Ни одно Р не суть S

(I) Некоторые S суть Р………………….(I) Некоторые Р суть S

 

 

Выделяющие суждения (общие и частные) обращаются по схеме:

(А) Все S и только S суть Р …………….(А) Все Р суть S

(А) Некоторые S и только S суть Р …….(А) Все Р суть S

 

Противопоставлением предикату называется такое непосредственное умозаключение, в котором в выводе субъектом является понятие, противоречащее предикату исходного суждения, а предикатом – субъект исходного суждения, при этом связка меняется на противоположную.

При этом следует помнить, что:

1) сначала нужно суждение превратить, а потом обратить.

2) Суждение I нельзя противопоставить предикату.

 

Схема противопоставления

(А) Все S суть Р …………….(Е) Ни одно не Р не есть S

(Е) Ни одно S не есть Р …….(I) Некоторые не Р суть S

(О) Некоторые S не суть Р….(