
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Завдання на розуміння мови математичних символівСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Конспект уроку Тема уроку. Прямі і площини в просторі. Мета уроку: сформувати уявлення про площину, простір, нескінченність; ознайомити учнів зі способами задання площини, розміщення площин і прямих у просторі. Література: 1. Бурда М.І., Тарасенкова Н.А. Геометрія 10кл. – К., 2010 2. Нелін Є.П. Геометрія 10 кл. – Х, 2010 Хід уроку І. Виклад матеріалу. Поняття простору і площини Досі ви вивчали геометрію площини — планіметрію. Сьогодні ознайомимося з геометрією простору — стереометрією. Так само, як і планіметрія, стереометрія оперує поняттями: точка, відрізок, промінь, пряма, та додається нове поняття — «площина». Щоб створити образ цього поняття, уявімо рух точки, прямої і площини. Точка рухається в одному напрямі, образом її руху є... (учні відповідають — пряма). Горизонтальна пряма рухається, скажімо, вертикально. Образом її руху стане..(площина, — відповідають учні). Площина рухається і заповнює простір. Зауважимо, що пряма, площина, простір нескінченні. З площинами ми зустрічаємося щодня, наприклад, моделлю площини може бути, скажімо, поверхня учнівського стола. Пригадаємо, як можуть розміщатися прямі на площині. (Учні відповідають.) Правильно, прямі можуть перетинатися і не перетинатися. Як же можна задати площину? (Учні відповідають.) Отже, площину можна задати: трьома точками, що не лежать на одній прямій, паралельними прямими, прямими, що перетинаються, прямою і точкою, що не лежить на цій прямій. Розміщення площин і прямих у просторі. Площини називаються паралельними, якщо вони не мають спільних точок. Запис: Площини перетинаються, якщо вони мають хоча б одну спільну точку. Площини перетинаються по прямій. Запис: Паралельні площини і площини, що перетинаються, утворюють видимий об'єм наших приміщень. У просторі, так само, як і на площині, пряма задається двома точками. Прямі можуть бути паралельними або перетинатися, тоді вони лежать в одній площині. Прямі в просторі, які лежать у різних площинах, та не паралельні і не перетинаються, називаються мимобіжними. Розміщення прямої і площини. Пряма і площина можуть перетинатися. Запис: Пряма може бути паралельною площині. Запис:
Пряма, яка перетинає площину, перпендикулярна до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині, і проходить через точку перетину. Запис: Відстанню від точки до площини називається довжина перпендикуляра, проведеного з цієї точки до площини. Дві площини, що перетинаються, називаються перпендикулярними, якщо третя площина, перпендикулярна до прямої перетину даних площин, перетинає їх по перпендикулярних прямих. II. Закріплення матеріалу. Задачі на розглядання Задача 1. Назвіть (рис. 1): а) точку перетину прямої АD і площини DD1C; б) лінію перетину площин АDD1і DD1С; в) в яких площинах лежить точка В; г)
Рис. 1 Рис. 2 Доведіть, що точки А, В, С і D лежать в одній площині. Задача 2. Назвіть (рис. 2): а) точку перетину прямої BDі площини АВС; б) лінію перетину площини АВD і СВD; в) в якій площині не лежить точка С. Прямі АВ і АС перетинаються з деякою прямою в точкахК і М відповідно. Доведіть, що М, К, С, і В лежать в одній площині. Задача 3. Назвіть (рис. 3): а) точку перетину прямої МС і площини ВKС; б) лінію перетину площин MLС і ВСK; в) в яких площинах лежить пряма МD. Доведіть, що точки А, В, С і D лежать в одній площині. Задача 4. Побудуйте лінію перетину (рис. 4): а) площини АВСі прямої МК; б)
Рис. 3 Рис. 4
Задачі на уяву 1. Чи можуть дві різні площини мати три спільні точки, що не лежать на одній прямій? 2. Чи можуть дві різні площини перетинатися по двох прямих? 3. Прямі а, b, c не належать одній площині, але проходять через одну точку. Скільки різних площин можна провести через ці прямі, взяті по дві? 4. Площини перетинаються по прямій а. Пряма b, що лежить у одній площині, перетинає іншу площину в точці А. Де лежить точка А? 5. Точки А і В та пряма СD не лежать в одній площині. Яке взаємне розміщення прямих CD i AB? ІІІ. Домашнє завдання. Вивчити опорний конспект, розв’язати задачі. Запишіть висловлення мовою символів: а) пряма а перетинає площину б) прямі КА і КВ перетинаються в точці К;
в) пряма КН перпендикулярна до прямої МС. На перетині прямих лежить точка К. Тестові завдання 1. а) Дано куб АВСDА1В1С1D1. яка з точок лежить у площині квадрата АВСD? 1) М; 2) К; 3) N; 4) Р. б) Дано тетраедр АВСS. Яка з точок не лежить у площині трикутника АВС?
2. а) Якій із вказаних площин куба не належить точка А? 1) ВСD; 2) А1С1С; 3) ВВ1А1; 4) ВСС1. б) Якій із вказаних площин тетраедра належить точка X? 1) ASB; 2) ASC; 3) BSC; 4) ABC. 4. а) Площини тетраедра АSС і АSВ перетинаються по прямій: 1) AS; 2) AB; 3) AC; 4) SC. б) Площини куба АВС і В1ВD перетинаються по прямій: 1) ВС; 2) ВD; 3) АВ; 4) ВВ1.
Академічний рівень Тема. Прямі та площини у просторі МЕТА Мета теми – закласти основи для навчання учнів конструюванню геометричних тіл, дослідженню їх властивостей і вимірюванню геометричних величин, що пов’язані з ними; продовжити реалізацію ідеї моделювання реальних об’єктів і відношень між ними за допомогою найпростіших просторових геометричних фігур і відповідних математичних відношень; сприяти розвитку в учнів навичок логічного виведення, уявлень про аксіоматичний метод. ОСНОВНІ ВИМОГИ В результаті вивчення теми учні повинні вміти: - встановлювати у просторі взаємне розміщення прямих і площин, зо-крема паралельність і перпендикулярність прямих, прямої і площини, двох площин; - будувати зображення фігур і на зображеннях виконувати нескладні побудови (елементів фігур, точок перетину прямої та площини, двох площин, переріз куба, тетраедра тощо); - обчислювати відстані і кути у просторі; - застосовувати відношення паралельності і перпендикулярності, а також вимірювання відстаней і кутів у просторі. ЗМІСТ ТЕМИ Аксіоми стереометрії та найпростіші наслідки з них. Взаємне розміщення двох прямих у просторі. Паралельність прямої та площини. Паралельність площин. Паралельне проектування та його властивості. Зображення фігур у стереометрії. Перпендикулярність прямої і площини. Перпендикулярність площин. Ортогональне проектування. Вимірювання відстаней у просторі. Вимірювання кутів у просторі. МЕТОДИЧНІ РЕКОМЕНДАЦІЇ Однією з головних особливостей викладання стереометрії повинно бути розумне поєднання наочно-геометричного та логічного у викладі. При вивченні основних понять і фактів, пов’язаних зі взаємним розміщенням прямих і площин, слід віддати перевагу синтетичному, наочно-геометричному викладенню, а потім використовувати вектори та координати для поглиблення та розширення знань учнів при вивченні прямих і площин у просторі. Такий підхід зберігає логічні зв’язки між зазначеними питаннями. Адже для вивчення поняття вектора у просторі і його властивостей використовується паралельність прямих і площин, для введення координат у просторі – перпендикулярність прямої і площини, перпендикулярність площин тощо. Формування просторових уявлень учнів є головним завданням даної теми. Тому важливе місце треба відвести їх навчанню зображати просторові фігури на площині і застосуванню цих зображень до розв’язування задач. І зробити це доцільно якомога раніше. Для ілюстрації розглядуваних понять і теорем доцільно використовувати найпростіші тіла, зокрема куб і тетраедр. Особливу увагу необхідно приділити реалізації прикладної спрямованості викладання теми. Головним в цьому є формування чітких уявлень про взаємовідношення властивостей геометричних об’єктів (прямих, площин) і відношень між ними і предметами навколишнього середовища.
Конспект уроку Тема уроку. Основні поняття стереометрії. Просторові тіла. Аксіоми стереометрії. Мета уроку: ознайомити учнів з основними поняттями стереометрії, сприяти формуванню в учнів уявлень про найпростіші просторові тіла, про аксіоматичний метод, розвитку навичок логічного виведення, а також застосування аксіом стереометрії та наслідків з них до розв’язування задач. Література: 1. Біляніна О.Я., Білянін Г.І., Швець В.О. Геометрія 10 клас: Академічний рівень. – К.: Генеза, 2010. 2. Погорєлов А. В. Геометрія 7-11 кл., Просвещение, 1989. Хід уроку І. Вступ У 10 класі починаємо вивчати новий розділ геометрії – стереометрію. У молодших класах вивчали такий розділ, як планіметрія, тобто всі фігури (точка, пряма, трикутник, трапеція тощо) вивчали на площині. Саму ж площину як фігуру не розглядали. Тестові завдання 1. а) Які з наведених фігур можуть бути тільки плоскими, а які — тільки просторовими? 1 ) круг; 2) куля; 3) квадрат; 4) куб; 5) прямокутний паралелепіпед; 6) ромб; 7) піраміда; 8) циліндр. б) Наведіть приклади плоских та просторових фігур з навколишнього оточення.
3. Дано зображення куба АВСDА1В1С1D1. Вкажіть: а) точки, що не належать грані АА1DD1; б) точки, що належать грані ВВ1С1С.
4. Дано зображення куба АВСDА1В1С1D1. Вкажіть: а) пряму перетину грані АА1D1D і нижньої основи; б) пряму перетину грані ВВ1С1С і нижньої основи. 5. а) Столяр за допомогою двох ниток перевіряє, чи буде стійким на рівній підлозі виготовлений стілець, що має чотири ніжки. Як для цього треба натягнути нитки? На яке теоретичне положення спирається така перевірка? б) Щоб поверхня розпилу чотирикутної балки була плоскою, тесля робить так: позначає на ребрі балки точку А та проводить від неї у потрібному напрямі дві прямі АВ і АС у суміжних площинах поверхні балки; потім скеровує пилку по намічених прямих. Поясніть, чому у такий спосіб одержимо плоску поверхню розпилу. 6. Дано зображення куба АВСDА1В1С1D1. Доведіть, що можна провести площину: а) через прямі АС і СС1; б) через прямі ВD і DD1. 7. а) Чи можуть дві площини мати тільки одну спільну точку? б) Чи можуть три площини мати тільки одну спільну точку?
Конспект уроку Тема уроку. Виникнення і розвиток стереометрії. Аксіоми та наслідки з них. Мета уроку: розширити і систематизувати відомості учнів про властивості основних геометричних фігур на площині і в просторі. Література: 1. Бевз Г.П. та ін. Геометрія: Підручник для 10-11 кл. з поглибленим вивч. математики. – К.: Освіта, 2000. Хід уроку І. Вступ Логічна побудова геометрії Кожна наука і кожний навчальний предмет у школі оперують певним колом понять, вивчають їх властивості і відношення між ними. Геометрія – це наука про властивості геометричних фігур, і вона має справу з такими поняттями, як геометрична фігура. – Які ви знаєте види фігур? Наприклад, трикутник, круг, куб. – Які відношення між фігурами вивчає геометрія? Такі відношення між фігурами, як рівність, подібність, паралельність, перпендикулярність. – Назвіть розглядувані перетворення фігур. Наприклад, симетрія, поворот, подібність. – З якими геометричними величинами має справу геометрія? Це довжини відрізка, кола, градусна міра кута, площа, об'єм. На відміну від інших наук геометрія має специфіку в своїй побудові. Вона побудована дедуктивно. – Що це означає? Дедукція (від лат. deduction – виведення) у широкому розумінні – це така форма мислення, коли нова думка виводиться суто логічно з деяких даних думок-посилань. У вужчому розумінні дедукція – це такий умовивід, внаслідок якого одержуються нові знання про предмети або групи предметів на основі вже наявних знань про досліджувані предмети. – Що вивчає планіметрія? Які її найпростіші фігури? У планіметрії вивчаються фігури на площині. Найпростішими фігурами в планіметрії є точка і пряма. Ці два поняття належать до первісних понять, яким домовились не давати означень і використовувати їх при означенні інших понять. Наприклад, серединним перпендикуляром до відрізка називається пряма, яка перпендикулярна до цього відрізка і проходить через його середину. Тут серединний перпендикуляр визначається через первісне поняття «пряма». Потреба в первісних поняттях і їх роль в геометрії саме і пов'язані з дедуктивним характером її побудови. Справді, в геометрії кожне нове поняття, крім первісних, означається або на основі первісних, або на основі раніше означених понять. Розглянемо ще один приклад. – Що називають квадратом? Як відомо, квадратом називають прямокутник, у якого всі сторони рівні. – Через яку фігуру означається прямокутник? Прямокутник визначається через паралелограм, у якого всі кути прямі. – Дайте означення паралелограма. Паралелограм визначається через чотирикутник. Крім точки і прямої, первісними поняттями планіметрії є поняття „належати” для точок і прямих, „лежати між” – для трьох точок прямої, „довжина відрізка”, „градусна міра кута”. Первісні поняття, як і більшість означуваних, походять від об'єктів, що існують реально, і є абстракцією від них. Наприклад, поняття „площина” походить від реальної поверхні кришки стола або поверхні озера. Однак площину ми уявляємо необмежене продовженою, вона не має товщини.
– Від якого реального об’єкта абстрагують пряму? Пряма образ туго натягнутої нитки або дроту. Проте пряма в геометрії не має кінців і уявляється необмежене продовженою, вона не має товщини. Крім первісних і означуваних понять геометрія оперує твердженнями, що виражають властивості понять. Вони бувають двох видів: аксіоми і теореми. Твердження, що виражають властивості найпростіших фігур (первісних понять) і приймаються без доведення, називаються аксіомами. Твердження, що виражають властивості геометричних фігур і доводяться, мають назву теорем. Потреба і роль аксіом теж спричинені дедуктивним характером побудови геометрії. Тут ми маємо аналогічну схему, бо кожне нове твердження доводиться на основі раніше відомого, вже доведеного твердження і т. д. Оскільки ланцюжок тверджень не може бути нескінченним, виникає потреба невелику їх кількість домовитись прийняти без доведення і використовувати при доведенні інших. – Проаналізуємо означення „Суміжні кути” з погляду того, через які раніше відомі поняття воно формулюється. Пригадаємо його. Два кути називаються суміжними, якщо одна їх сторона спільна, а інші сторони цих кутів є додатковими півпрямими. – Через які поняття воно означається? Воно означається через поняття сторона кута та півпряма. – Виділимо основні поняття, відношення та величини. Основні поняття: точка і пряма, основні відношення: лежати між, лежати на, основні величини: градусна міра кута. – Як висновок, розглянемо наступну схему побудови геометрії. 1. Перелічуються первісні (неозначувані) поняття. 2. Формулюються аксіоми про властивості первісних понять. 3. За допомогою первісних та раніше означених понять формулюються означення нових понять. 4. На основі аксіом, доведених раніше тверджень і означень доводяться нові твердження. ІІІ. Задачі на доведення Задача 1. Точки А, В, С і D не лежать в одній площині. Доведіть, що прямі АВ і СD не перетинаються. Доведення. – Скористаємось методом від супротивного. – Яке можемо зробити припущення? – Маємо дві прямі, що перетинаються. Яке з щойно вивчених тверджень можемо застосувати? – Якщо прямі АВ і СD визначають площину – У чому полягає отримане протиріччя? Нехай прямі АВ і СD перетинаються, тоді за аксіомою С3: Задача 2. Чотири точки не лежать в одній площині. Чи можуть будь-які три з них лежати на одній прямій. Доведення. – Яке можна висунути припущення? – Яке відоме вам твердження можна застосувати? – З якою умовою ми отримали протиріччя? Нехай три точки лежать на одній прямій, а четверта не належить цій прямій. Тоді за теоремою-наслідком 1 можна провести єдину площину, якій належить дані пряма і точка. Це означає, що задані умовою чотири точки належать одній площині. За умовою задачі це не можливо. Значить будь-які три з цих точок не можуть лежати на одній прямій. IV. Підсумок уроку Сьогоднішній урок було присвячено ідеї дедуктивної побудови геометрії, походженню та ролі первісних понять і аксіом, ми пригадали аксіоми планіметрії, ознайомилися з аксіомами стереометрії та наслідками з них. Завершити урок хочеться прикладами використання аксіом та їх наслідків у виробничій діяльності людини. 1) Тесляр перевіряє, чи розміщуються кінці ніжок стола в одній площині, від чого залежить стійкість стола. Він натягує нитки на кінці ніжок і перевіряє, чи перетинаються вони (аксіома С3). 2) Тесляр перевіряє якість поверхні стола, що виготовляється, прикладаючи до кришки в різних напрямках лінійку. Якщо між лінійкою і кришкою стола немає просвітів, то стіл виготовлено якісно (теорема 2). 3) На теоремі 3 ґрунтується будова штативів для фотоапаратів і різних геодезичних приладів. Кінці ніжок штативів належать одній площині, внаслідок чого прилад займає стійке положення. Тестові завдання 2.
3. Як розмістити три прямі так, щоб вони утворили 12 прямих кутів? 4. Чи вірно, що пряма, яка має з колом тільки одну спільну точку, є дотичною до кола в цій точці: 1) на площині; 2) у просторі? 4. Довести, що через дві довільні точки можна провести хоча б одну площину. 5. Чи можна стверджувати, що всі точки кола належать площині, якщо це коло має з даною площиною: 1) дві спільні точки; 2) три спільні точки. 6. Через три точки можна провести дві різні площини. Як розташовані ці точки?
Конспект уроку Тема уроку. Прямі і площини в просторі. Мета уроку: сформувати уявлення про площину, простір, нескінченність; ознайомити учнів зі способами задання площини, розміщення площин і прямих у просторі. Література: 1. Бурда М.І., Тарасенкова Н.А. Геометрія 10кл. – К., 2010 2. Нелін Є.П. Геометрія 10 кл. – Х, 2010 Хід уроку І. Виклад матеріалу. Поняття простору і площини Досі ви вивчали геометрію площини — планіметрію. Сьогодні ознайомимося з геометрією простору — стереометрією. Так само, як і планіметрія, стереометрія оперує поняттями: точка, відрізок, промінь, пряма, та додається нове поняття — «площина». Щоб створити образ цього поняття, уявімо рух точки, прямої і площини. Точка рухається в одному напрямі, образом її руху є... (учні відповідають — пряма). Горизонтальна пряма рухається, скажімо, вертикально. Образом її руху стане..(площина, — відповідають учні). Площина рухається і заповнює простір. Зауважимо, що пряма, площина, простір нескінченні. З площинами ми зустрічаємося щодня, наприклад, моделлю площини може бути, скажімо, поверхня учнівського стола. Пригадаємо, як можуть розміщатися прямі на площині. (Учні відповідають.) Правильно, прямі можуть перетинатися і не перетинатися. Як же можна задати площину? (Учні відповідають.) Отже, площину можна задати: трьома точками, що не лежать на одній прямій, паралельними прямими, прямими, що перетинаються, прямою і точкою, що не лежить на цій прямій. Розміщення площин і прямих у просторі. Площини називаються паралельними, якщо вони не мають спільних точок. Запис: Площини перетинаються, якщо вони мають хоча б одну спільну точку. Площини перетинаються по прямій. Запис: Паралельні площини і площини, що перетинаються, утворюють видимий об'єм наших приміщень. У просторі, так само, як і на площині, пряма задається двома точками. Прямі можуть бути паралельними або перетинатися, тоді вони лежать в одній площині. Прямі в просторі, які лежать у різних площинах, та не паралельні і не перетинаються, називаються мимобіжними. Розміщення прямої і площини. Пряма і площина можуть перетинатися. Запис: Пряма може бути паралельною площині. Запис: Пряма, яка перетинає площину, перпендикулярна до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині, і проходить через точку перетину. Запис: Відстанню від точки до площини називається довжина перпендикуляра, проведеного з цієї точки до площини. Дві площини, що перетинаються, називаються перпендикулярними, якщо третя площина, перпендикулярна до прямої перетину даних площин, перетинає їх по перпендикулярних прямих. II. Закріплення матеріалу. Задачі на розглядання Задача 1. Назвіть (рис. 1): а) точку перетину прямої АD і площини DD1C; б) лінію перетину площин АDD1і DD1С; в) в яких площинах лежить точка В; г)
Рис. 1 Рис. 2 Доведіть, що точки А, В, С і D лежать в одній площині. Задача 2. Назвіть (рис. 2): а) точку перетину прямої BDі площини АВС; б) лінію перетину площини АВD і СВD; в) в якій площині не лежить точка С. Прямі АВ і АС перетинаються з деякою прямою в точкахК і М відповідно. Доведіть, що М, К, С, і В лежать в одній площині. Задача 3. Назвіть (рис. 3): а) точку перетину прямої МС і площини ВKС; б) лінію перетину площин MLС і ВСK; в) в яких площинах лежить пряма МD. Доведіть, що точки А, В, С і D лежать в одній площині. Задача 4. Побудуйте лінію перетину (рис. 4): а) площини АВСі прямої МК; б)
Рис. 3 Рис. 4
Задачі на уяву 1. Чи можуть дві різні площини мати три спільні точки, що не лежать на одній прямій? 2. Чи можуть дві різні площини перетинатися по двох прямих? 3. Прямі а, b, c не належать одній площині, але проходять через одну точку. Скільки різних площин можна провести через ці прямі, взяті по дві? 4. Площини перетинаються по прямій а. Пряма b, що лежить у одній площині, перетинає іншу площину в точці А. Де лежить точка А? 5. Точки А і В та пряма СD не лежать в одній площині. Яке взаємне розміщення прямих CD i AB? Завдання на розуміння мови математичних символів 1. Дано вирази
1) Серед цих виразів знайдіть помилкові. 2) Який із записів відповідає висловленню: а) площини перетинаються по прямій а; б) точка А є точкою перетину площини 2. Як можуть розміщатися прямі а та АВ у площинах ІІІ. Домашнє завдання. Вивчити опорний конспект, розв’язати задачі. Запишіть висловлення мовою символів: а) пряма а перетинає площину б) прямі КА і КВ перетинаються в точці К; в) пряма КН перпендикулярна до прямої МС. На перетині прямих лежить точка К. Тестові завдання 1. а) Дано куб АВСDА1В1С1D1. яка з точок лежить у площині квадрата АВСD? 1) М; 2) К; 3) N; 4) Р. б) Дано тетраедр АВСS. Яка з точок не лежить у площині трикутника АВС?
2. а) Якій із вказаних площин куба не належить точка А? 1) ВСD; 2) А1С1С; 3) ВВ1А1; 4) ВСС1. б) Якій із вказаних площин тетраедра належить точка X? 1) ASB; 2) ASC; 3) BSC; 4) ABC. 4. а) Площини тетраедра АSС і АSВ перетинаються по прямій: 1) AS; 2) AB; 3) AC; 4) SC. б) Площини куба АВС і В1ВD перетинаються по прямій: 1) ВС; 2) ВD; 3) АВ; 4) ВВ1.
Академічний рівень Тема. Прямі та площини у просторі МЕТА Мета теми – закласти основи для навчання учнів конструюванню геометричних тіл, дослідженню їх властивостей і вимірюванню геометричних величин, що пов’язані з ними; продовжити реалізацію ідеї моделювання реальних об’єктів і відношень між ними за допомогою найпростіших просторових геометричних фігур і відповідних математичних відношень; сприяти розвитку в учнів навичок логічного виведення, уявлень про аксіоматичний метод. ОСНОВНІ ВИМОГИ В результаті вивчення теми учні повинні вміти: - встановлювати у просторі взаємне розміщення прямих і площин, зо-крема паралельність і перпендикулярність прямих, прямої і площини, двох площин; - будувати зображення фігур і на зображеннях виконувати нескладні побудови (елементів фігур, точок перетину прямої та площини, двох площин, переріз куба, тетраедра тощо); - обчислювати відстані і кути у просторі; - застосовувати відношення паралельності і перпендикулярності, а також вимірювання відстаней і кутів у просторі. ЗМІСТ ТЕМИ Аксіоми стереометрії та найпростіші наслідки з них. Взаємне розміщення двох прямих у просторі. Паралельність прямої та площини. Паралельність площин. Паралельне проектування та його властивості. Зображення фігур у стереометрії. Перпендикулярність прямої і площини. Перпендикулярність площин. Ортогональне проектування. Вимірювання відстаней у просторі. Вимірювання кутів у просторі. МЕТОДИЧНІ РЕКОМЕНДАЦІЇ Однією з головних особливостей викладання стереометрії повинно бути розумне поєднання наочно-геометричного та логічного у викладі. При вивченні основних понять і фактів, пов’язаних зі взаємним розміщенням прямих і площин, слід віддати перевагу синтетичному, наочно-геометричному викладенню, а потім використовувати вектори та координати для поглиблення та розширення знань учнів при вивченні прямих і площин у просторі. Такий підхід зберігає логічні зв’язки між зазначеними питаннями. Адже для вивчення поняття вектора у просторі і його властивостей використовується паралельність прямих і площин, для введення координат у просторі – перпендикулярність прямої і площини, перпендикулярність площин тощо. Формування просторових уявлень учнів є головним завданням даної теми. Тому важливе місце треба відвести їх навчанню зображати просторові фігури на площині і застосуванню цих зображень до розв’язування задач. І зробити це доцільно якомога раніше. Для ілюстрації розглядуваних понять і теорем доцільно використовувати найпростіші тіла, зокрема куб і тетраедр. Особливу увагу необхідно приділити реалізації прикладної спрямованості викладання теми. Головним в цьому є формування чітких уявлень про взаємовідношення властивостей геометричних об’єктів (прямих, площин) і відношень між ними і предметами навколишнього середовища. Конспект уроку Тема уроку. Основні поняття стереометрії. Просторові тіла. Аксіоми стереометрії. Мета уроку: ознайомити учнів з основними поняттями стереометрії, сприяти формуванню в учнів уявлень про найпростіші просторові тіла, про аксіоматичний метод, розвитку навичок логічного виведення, а також застосування аксіом стереометрії та наслідків з них до розв’язування задач. Література: 1. Біляніна О.Я., Білянін Г.І., Швець В.О. Геометрія 10 клас: Академічний рівень. – К.: Генеза, 2010. 2. Погорєлов А. В. Геометрія 7-11 кл., Просвещение, 1989. Хід уроку І. Вступ У 10 класі починаємо вивчати новий розділ геометрії – стереометрію. У молодших класах вивчали такий розділ, як планіметрія, тобто всі фігури (точка, пряма, трикутник, трапеція тощо) вивчали на площині. Саму ж площину як фігуру не розглядали.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 604; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.184.57 (0.018 с.) |

 .
.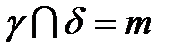 .
. .
. . У цьому випадку пряма і площина спільних точок не мають.
. У цьому випадку пряма і площина спільних точок не мають.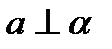 .
. в точці В;
в точці В;



 , то який висновок можемо зробити щодо точок?
, то який висновок можемо зробити щодо точок? , а це означає, що точки А, В, С і D лежать в одній площині. Отримали протиріччя з умовою задачі. Значить прямі АВ і СD не перетинаються.
, а це означає, що точки А, В, С і D лежать в одній площині. Отримали протиріччя з умовою задачі. Значить прямі АВ і СD не перетинаються.
 і прямої а?
і прямої а? і
і  ? Запишіть мовою символів.
? Запишіть мовою символів.


