
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Іі. Пояснення нового матеріалу
Основні поняття стереометрії Стереометрія – це розділ геометрії, що вивчає фігури у просторі. Найпростішими фігурами простору є: - точка: А, В, С,... - пряма: а, в, с,... - площина:
площина (АВС)
Взагалі площини позначаються грецькими літерами:

Введемо основні позначення: АВ – пряма; [АВ] – відрізок; [АВ) – промінь з початком в точці А; |АВ| – довжина відрізку; А є а – точка А належить прямій а; А (АВС) – площина; А є А АВ АВ {А; а} а ∩ в = К – прямі а і в перетинаються в точці К; а ∩
Властивості геометричних фігур в стереометрії будемо встановлювати шляхом доведення теорем. Але щоб доводити теореми, необхідно спиратися на деякі вихідні твердження. Такі твердження називають аксіомами. Оскільки на цих твердженнях ґрунтується доведення теорем стереометрії, то вони отримали назву – група аксіом С. С1. Яка б не була площина, існують точки, що належать цій площині, і точки, що не належать цій площині.
С2. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку.
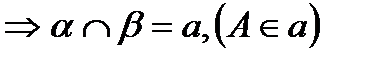
С3. Якщо дві різні прямі мають спільну точку, то через них можна провести площину, і притому тільки одну.
 {а, в}, {а, в},
Таким чином, група аксіом С, а також ті аксіоми, що вивчались у молодших класах у розділі планіметрія, і складають систему аксіом стереометрії. Зауважимо, що не всі аксіоми планіметрії механічно переносяться до системи аксіом стереометрії. Прикладом тому є аксіома ІV: пряма розбиває площину на дві півплощини. Проілюструємо її на рисунку.
таким чином: пряма, що належить площині, розбиває її на дві півплощини.
Також нагадаємо аксіому І планіметрії, оскільки вона знадобиться нам для доведення теорем. І. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать цій прямій. Через будь-які дві точки можна провести пряму, і притому тільки одну. Наслідки з аксіом Теорема 1. Через пряму і точку, що не належить даній прямій, можна провести площину, і притому тільки одну.
 АВ. АВ.
 {АВ, С}; {АВ, С};
2) Доведення 1) Проведемо пряму АС (аксіома І). АС і АВ різні, оскільки С 2) Доведемо єдиність (методом від супротивного). Нехай існує ще одна площина Теорему доведено. Теорема 2. Якщо дві точки прямої належать площині, то вся пряма належить цій площині. А
В Опорна задача. Якщо дві площини мають дві спільні точки, то вони перетинаються по прямій, що містить ці точки.
Теорема 3. Через три точки, що не лежать на одній прямій, можна провести площину, і притому тільки одну.
 а. а.
 ; ;
2) Доведення. 1) Проведемо прямі АВ і АС (аксіома І), вони різні, оскільки 2) Доведемо єдиність. За теоремою 2: Теорему доведено. Побудова перерізів просторових фігур Перерізом многогранника називається многокутник, що утворюється при перетині многогранника з площиною. Щоб будувати прості перерізи, слід вміти будувати:
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.231.245 (0.012 с.) |
 ,..., (АВС).
,..., (АВС).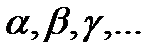 . Площина, як і пряма, нескінченна. На малюнку позначаємо тільки частину площини, але уявляємо її необмежено продовженою у всі сторони.
. Площина, як і пряма, нескінченна. На малюнку позначаємо тільки частину площини, але уявляємо її необмежено продовженою у всі сторони.
 а – точка А не належить прямій а;
а – точка А не належить прямій а; – точка належить площині
– точка належить площині  ;
; – точка не належить площині
– точка не належить площині  – пряма АВ належить площині
– пряма АВ належить площині  ;
; – пряма АВ не належить площині
– пряма АВ не належить площині  – точка А та пряма а належать площині
– точка А та пряма а належать площині  ; точка А та пряма а визначають площину
; точка А та пряма а визначають площину  ;
;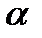 = N – пряма а і площина
= N – пряма а і площина  перетинаються в точці N;
перетинаються в точці N;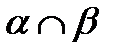 = АВ – площини
= АВ – площини  і
і  перетинаються по прямій АВ.
перетинаються по прямій АВ.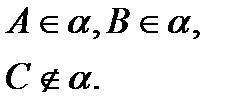
 – єдина.
– єдина. єдина.
єдина. АВ. За аксіомою С3: АВ і АС визначають площину
АВ. За аксіомою С3: АВ і АС визначають площину 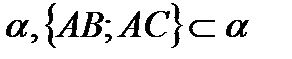 .
. , що проходить через АВ і точку С. За аксіомою С2: точки А, В і С повинні лежати на одній прямій. Це суперечить умові, що С
, що проходить через АВ і точку С. За аксіомою С2: точки А, В і С повинні лежати на одній прямій. Це суперечить умові, що С  АВ. Припущення не вірне.
АВ. Припущення не вірне. |
| .
. |
| |
|
 |
| – єдина.
– єдина. а. За аксіомою С3: через прямі АВ і АС можна провести площину
а. За аксіомою С3: через прямі АВ і АС можна провести площину  .
. . За аксіомою С3 така площина єдина.
. За аксіомою С3 така площина єдина.


