
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логічне заперечення (інверсія)Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Логічне заперечення (інверсія, операція «НЕ») є функцією одного аргументу. Дану функцію описує наступна словесна форма: результат приймає значення «0», якщо аргумент рівний «1» і навпаки. У таблиці 2.1 зведені: табличний опис, символьні позначення, формульний опис і позначення електронного елемента, що реалізовує логічну функцію «ЗАПЕРЕЧЕННЯ». У даній таблиці і в подальших таблицях, що описують інші функції, аргументи позначаються через Таблиця 2.1 – Логічне заперечення
Логічне множення (кон'юнкція) Логічне множення (кон'юнкція, «логічне І») є функцією двох та більше аргументів. Дану функцію описує наступна словесна форма: результат приймає значення «1», тільки якщо всі аргументи рівні «1», інакше - «0». Або по іншому: результатом логічного множення є «0» якщо хоч би один з аргументів рівний «0» і результат рівний одиниці в протилежному випадку. Логічне множення характеризує таблиця 2.2. Логічне складання (диз'юнкція) Логічне складання (диз'юнкція, «логічне АБО») є функцією двох і більше аргументів. Дану функцію описує наступна словесна форма: результат приймає значення «1», якщо хоч би один аргумент рівний «1», інакше - «0». Або по іншому: результат логічного складання рівний «0» тільки якщо всі аргументи рівні «0» і рівний «1» в іншому випадку. Функцію логічного складання характеризує таблиця 2.3.
Таблиця 2.2 – Логічне множення
Таблиця 2.3 – Логічне складання
У позначенні логічного елементу знак
Аксіоми і закони булевої алгебри Аксіоми булевої алгебри визначають наступні вирази:
Як і в звичайній алгебрі в алгебрі логіки діють наступні закони: 1) переміщувальний (комутативний)
2) сполучний (асоціативний)
3) розподільний (дистрибутивний)
Слід звернути увагу на відсутність формальної аналогії між розподільними законами в звичайній і булевій алгебрі. Крім того в алгебрі логіки діють такі закони: 1) закон поглинання
2) закон доповнення
3) закон нульової множини
4) закон універсальної множини
5) закон повторення
6) закон подвійного заперечення
7) закон заперечення (закон Моргана)
8) закон склеювання
Закон Моргана показує, що розглянутий класичний набір елементарних логічних функцій надмірний. Використовуючи тільки пару логічних функцій, а саме «ЗАПЕРЕЧЕННЯ» і одну з функцій двох змінних («логічне І» або «логічне АБО») можна визначити решту всіх логічних функцій. Ця властивість використовується при побудові електронних логічних елементів. Базові електронні елементи Суперпозиція функцій «ЗАПЕРЕЧЕННЯ» і «логічне І» породжують функцію «І-НЕ» (штрих Шеффера):
А суперпозиція функцій «ЗАПЕРЕЧЕННЯ» і «логічне АБО» породжують функцію «АБО-НЕ» (стрілка Пірса):
Опис елементів «І-НЕ» і «АБО-НЕ» приведено відповідно в таблицях 2.4 і 2.5. Таблиця 2.4 – Логічне «І-НЕ»
Таблиця 2.5 – Логічне «ІЛІ-НЕ»
Кожна з цих функцій може бути базисом для алгебри логіки, тобто через кожну з даних функцій (без використання інших) може бути виражений весь набір всіляких логічних функцій. Ця чудова властивість служить основою для побудови серій логічних мікросхем, зокрема мікропроцесорів і мікроконтролерів. У електроніці це означає, що для реалізації всього різноманіття схем перетворення сигналів, що представляють логічні значення, досить одного або декількох типових елементів. Кожна з серій цифрових мікросхем базується на дискретних електронних елементах, званих базовими. Елемент «І-НЕ», що реалізує функцію Шеффера (штрих Шеффера), використовується при побудові інтегральних мікросхем ТТЛ-структури. Елемент «АБО-НЕ» (стрілка Пірса) використовується в інтегральних мікросхемах к ‑ МОП структури. Використання функцій, що не входять в визначений базис (функціональна надмірність), дозволяє істотно скоротити складність схем, що реалізують логічні вирази, і тим самим підвищити їх надійність. Тому базові елементи служать основою для побудови інших електронних елементів, що реалізують всі необхідні логічні функції. Об'єднуючи на одному кристалі базові елементи отримують мікросхеми, що реалізують функції "І" (конъюнктор), "АБО" (дизъюнктор), "НЕ" (інвертор) та інші. Серії цифрових мікросхем включають велику безліч елементів, що реалізоють як прості та і дуже складні логічні перетворення сигналів. Мінімальність і надмірність - важливі аспекти теорії інформації. Як факт: вимірювання надмірності російської мови дали близько 80%. У сленгах (наприклад, мові авіадиспетчерів) надмірність ще вище. Завершуючи тему базисів слід зазначити, що в «основний» набір електронних логічних елементів і функцій мов програмування зазвичай включають крім кон'юнкції, диз'юнкції, заперечення і ще одну логічну функцію "СУМА ПО МОДУЛЮ 2". Це пояснюється цілою низкою чудових властивостей цієї логічної функції.
Функція «СУМА ПО МОДУЛЮ 2» Логічна функція «СУМА ПО МОДУЛЮ 2» для двох аргументів задається таблицею 2.6. Таблиця 2.6 – Функція «СУМА ПО МОДУЛЮ 2»
Дана функція називається «СУМА ПО МОДУЛЮ 2», тому що обчислюється як залишок від ділення суми своїх аргументів на 2. Перевіримо дане твердження по рядках таблиці 2.6: 1) 2) 3) 4) Таким чином, значення залишків у виразах вище співпадають із значеннями в останньому стовпці таблиці 2.6. Функцію «СУМА ПО МОДУЛЮ 2» ще називають «Виключне АБО», а так само «НЕРІВНОЗНАЧНІСТЬ». Дійсно «1» з'являється в останньому стовпці таблиці 2.6 при неспівпаданні аргументів Неоднозначність технічних і навіть логічних термінів йде від неоднозначності розмовної мови. Наприклад, в граматиці російської мови (та й англійської також) не розрізняються «Виключає АБО» і просто «АБО». Так, у фразі «сніг чи вітер...» союз «чи» (коротка форма «або») має значення диз'юнкції, а у вітанні «гаманець чи життя» (як і в напутті «зі щитом чи на щиті»), той же союз виражає вже «виключне АБО». Насправді, функції «виключне АБО», «НЕРІВНОЗНАЧНІСТЬ» і «СУМА ПО МОДУЛЮ 2» - різні функції, ідентичні тільки у разі двох аргументів. Таблиця 2.7 представляє ці функції для випадку трьох аргументів. Таблиця 2.7 – Тернарні функції «СУМА ПО МОДУЛЮ 2»,
Включення функції «СУМА ПО МОДУЛЮ 2» в набір «популярні» викликано її чудовими властивостями. По-перше, при інвертуванні одного з аргументів ця функція також інвертується. По-друге, ця функція показує, коли аргументи не рівні (а при інвертуванні одного з аргументів - коли рівні). По-третє, вона дозволяє проводити кероване інвертування: при нульовому аргументі інший аргумент не міняється, при одиничному ж значенні другий аргумент інвертується. Нарешті, повторне застосування цієї функції повертає до початкового значення аргументу: якщо У графіці ця функція застосовується при виведенні спрайту на картинку - повторне її застосування прибирає спрайт з картинки. Також ця функція використовується в криптографії - одна з схем шифрування полягає в накладенні якогось коду на потік даних через функцію «СУМА ПО МОДУЛЮ 2». Зашифрований таким чином потік на початковий потік не схожий, але може бути легко відновлений повторним застосуванням шифруючого коду.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 547; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.33.239 (0.01 с.) |

 , а результат застосування функції через
, а результат застосування функції через  .
.










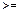 часто опускають, залишаючи позначення у вигляді 1.
часто опускають, залишаючи позначення у вигляді 1. (2.1)
(2.1) (2.2)
(2.2)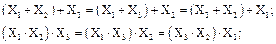 (2.3)
(2.3) (2.4)
(2.4) (2.5)
(2.5)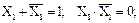 (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8) (2.9)
(2.9) (2.10)
(2.10) (2.11)
(2.11) (2.12)
(2.12) (2.13)
(2.13) (2.14)
(2.14)








 ;
; ;
; ;
; .
.
 , то
, то  і
і  .
.


