
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Елементарні логічні функції (операції)Содержание книги
Поиск на нашем сайте
Логічні функції можна виразити через елементарні логічні функції. Розглянемо найпоширеніші елементарні операції над двома логічними величинами. Операція логічного додавання (диз'юнкція). Операція логічного додавання позначається знаком «+» або «v». Логічна функція, що відповідає операції логічного додавання, називається функцією АБО. Запишемо логічну операцію додавання для всіх можливих значень аргументів:
Результат операції логічного додавання має значення 0 тільки у тому випадку, якщо обидва аргументи мають значення О, а значення 1 — якщо хоча б один із аргументів мав значення 1. Співвідношення 5.1 зручно подати у вигляді таблиці.
Таблиця 5.1
Операція логічного множення (кон'юнкція). Операція логічного множення позначається знаком математичного множення, тобто крапкою, яку можна не писати, або символом &. Логічна функція, що відповідає операції логічного множення, називається функцією І. Запишемо логічну операцію множення для всіх можливих значень аргументів:
Результат операції логічного множення має значення 1 тільки у тому випадку, якщо обидва аргументи мають значення 1, а значення 0 — якщо хоча б один з аргументів мав значення 0. Співвідношення 5.15 зручно подати у вигляді таблиці.
Таблиця 5.2
Операція логічного заперечення (інверсія). Операція логічного заперечення позначається рискою над ім'ям змінної
Запишемо співвідношення 5.16 у вигляді таблиці:
Таблиця 5.3
Властивості логічних операцій Операції логічного додавання (диз'юнкції) і множення (кон'юнкції) мають певні властивості, які визначаються тотожностями. Довести ці тотожності можна, наприклад, за допомогою таблиць істинності. Розглянемо найважливіші властивості логічних операцій:
- комутативність
- асоціативність
- дистрибутивність
- ідемпотентність
- поглинання
- склеювання
- правило де Морган
- правило де Морган
За допомогою співвідношень 5.17 - 5.30 можна виконувати тотожні перетворення логічних виразів і функцій для їх спрощення. Виконуючи тотожні перетворення, слід дотримуватися послідовності у виконанні операцій: у першу чергу виконуються операція заперечення, в другу — кон'юнкції, у третю — диз'юнкції. Якщо необхідно змінити послідовність виконання операцій, то застосовують дужки.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.121 (0.008 с.) |

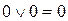
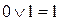
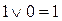
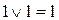 (14)
(14)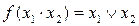
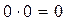
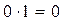
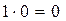
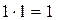 (5,15)
(5,15)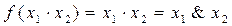
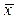 . Запишемо операцію логічного заперечення для всіх можливих значень аргументу
. Запишемо операцію логічного заперечення для всіх можливих значень аргументу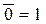
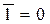 (5,16)
(5,16)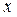
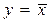
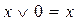
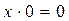 (5,17)
(5,17)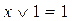
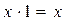 (5,18)
(5,18)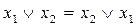
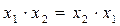 (5,19)
(5,19)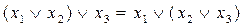
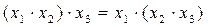 (5,20)
(5,20)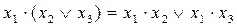
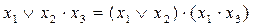 (5,21)
(5,21)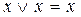
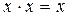 (5,22)
(5,22)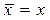 (5,23)
(5,23)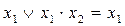
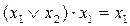 (5,24)
(5,24)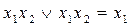
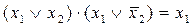 (5,25)
(5,25)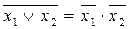
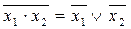 (5,26)
(5,26)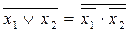
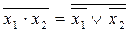 (5,27)
(5,27)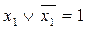
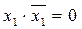 (5,28)
(5,28)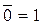
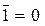 (5,29)
(5,29)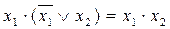
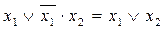 (5,30)
(5,30)


