
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функціонально повні системи елементарних функційСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сукупність елементарних логічних функцій, якими можна представити або через які можна виразити логічну функцію довільного ступеня складності, складають функціонально повну систему елементарних функцій. Операції логічного додавання, множення й заперечення складають функціонально повну систему логічних функцій. Це означає, що будь-яку логічну функцію довільної складності можна виразити через ці три логічні функції. Крім розглянутих логічних функцій диз'юнкції, і кон'юнкції й заперечення, існують інші функціонально повні системи елементарних функцій. Функція Шефера (штрих Шефера). Функцію Шефера двох аргументів, яку позначають
Таблиця 5.4
Як випливає з таблиці інтенсивності, функція Шефера має значення 0 тільки тоді, якщо обидва аргументи мають значення 1, у решті ж випадків вона має значення 1, тому цю функцію називають запереченням кон'юнкції, тому що Функція Шефера складає функціонально повну систему елементарних логічних функцій, тобто будь-яку логічну функцію можна виразити через функцію Шефера. Для того щоб довести це» достатньо виразити через функцію Шефера елементарні функції заперечення, кон'юнкції й диз'юнкції, що складають функціонально повну систему логічних функцій. Функція заперечення виражається через функцію Шефера таким чином:
У перетвореннях 5.17-5.30 використовувалися правило де Моргана та властивість ідемпотентності. Функцію кон'юнкції виражають через функцію Шефера, використовуючи властивості 5.23, 5.25, 5.26
Функцію диз'юнкції виражають через функцію Шефера, використовуючи властивості 5.31, 5.23, 5.24
Функція Пірса (стрілка Пірса). Функція Пірса двох змінних, яка позначається
Таблиця 5.5
Стрілка Пірса, як і функція Шефера, складає функціонально повну систему елементарних логічних функцій, тобто можна будь-яку логічну функцію виразити через стрілку Пірса. Спрощення логічних виразів
Логічний вираз або функцію можна представити у різних формах, використовуючи функціонально повну систему елементарних логічних функцій. У цифрових пристроях обробки інформації, зокрема у комп'ютері, логічні функції реалізуються за допомогою логічних елементів, тому для зменшення апаратурних затрат дуже важливо максимально спростити логічну функцію і знайти її форму з мінімальною кількістю операцій. Довільний логічний вираз можна звести до канонічної форми — суми добутків змінних, причому в кожен добуток входить або сама змінна, або її заперечення. Така канонічна форма логічного виразу носить назву диз'юнктивна нормальна форма (ДНФ). Наведемо кілька прикладів диз'юнктивних нормальних форм логічних виразів:
Таблиця 5.6
Таблиця 5.7
Другою канонічною формою, до якої можна звести будь-який логічний вираз, є добуток, сум логічних змінних, причому у кожну суму входить або сама змінна, або її заперечення. Така канонічна форма логічного виразу носить назву кон'юнктив-на нормальна форма (КНФ). Наведені вище логічні функції
Можна показати, що для будь-якого логічного виразу існує тільки одна диз'юнктивна нормальна форма і тільки одна кон'юнктивна нормальна форма. Спрощувати логічні вирази можна за допомогою послідовних тотожних логічних перетворень 5.17 - 5.30. Наприклад, застосувавши до першого і другого, а також до третього й четвертого доданків функції Крім тотожних перетворень, для спрощення логічних виразів, у яких кількість аргументів не перевищує шести, доцільно застосовувати так звані карти Карно. Карти Карно — це спеціальна таблиця істинності, рядки й стовпці якої відповідають усім можливим комбінаціям значень не більше двох змінних, причому ці комбінації змінних розміщені у такій послідовності, що дві сусідні комбінації, відповідно і дві сусідні клітинки таблиці відрізняються значенням тільки однієї змінної. Клітинки, розміщені на краю таблиці, також вважаються сусідніми. У ті клітинки карти Карно, які відповідають доданкам диз'юнктивної нормальної форми, записуються одиниці, у решту ж клітинок — записуються нулі. Сусідні клітинки з одиницями об'єднують у блоки по 2, 4, 8,... одиниць. Кожному блоку одиниць на карті Карно відповідає один доданок у диз'юнктивній формі функції, причому у блоках з двох одиниць кількість множників у доданку на одиницю менша кількості змінних, у блоках із чотирьох одиниць — на дві одиниці менша і т.д. Запишемо для прикладу карту Карно для функції
Таблиця 5.8
Об'єднавши одиниці на карті Карно у два блоки, отримуємо спрощений вираз для функції
Порівнюючи вирази (5.40) і (5.41), отримані в результаті спрощення різними методами, робимо висновок, що вони однакові. Логічні елементи Логічні елементи — це елементарні пристрої цифрової техніки, призначені для реалізації елементарних операцій над логічними змінними. Для реалізації операцій над логічними змінними, які можуть мати тільки два значення — 0 і 1, застосовують технічні пристрої, що можуть перебувати в одному з двох станів. Такими технічними пристроями є різного роду ключові елементи, які можуть перебувати в одному з двох станів: увімкнено й вимкнено. Ключові елементи можуть мати різну фізичну природу: пневматичний ключовий елемент — це клапан на пневмопроводі, який може перебувати у двох станах — закритому й відкритому; гідравлічний ключовий елемент — це клапан на трубопроводі з рідиною, який також може бути або відкритий, або закритий. Відомі пристрої, що виконують доволі складні логічні операції, побудовані на основі пневматичних ключових елементів. Однак найпоширенішими є логічні пристрої на основі електричних ключових елементів. Електричний ключ може бути механічної дії, коли електричне коло замикається чи розмикається вручну за допомогою електричного вимикача чи кнопки. Електричний ключ механічної дії застосовується для реалізації найпростіших логічних функцій на передніх панелях електричних пристроїв і вимірювальних приладів, задаючи різноманітні режими їх роботи. Більш досконалим електричним ключем є електромагнітне реле. До винайдення і широкого застосування електронних ключових елементів електромагнітні реле були основним елементом для реалізації пристроїв обробки цифрової інформації. На сучасному етапі розвитку цифрової техніки логічні елементи реалізуються на основі цифрових ключових елементів, або скорочено — цифрових ключів. Для створення цифрових ключів застосовуються біполярні й уніполярні (польові) транзистори, виготовлені за інтегральною технологією на кристалі напівпровідникового матеріалу, здебільшого кремнію.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.120.251 (0.012 с.) |

 , можна задати таблицею інтенсивності (табл.. 5,4)
, можна задати таблицею інтенсивності (табл.. 5,4) . (5,31)
. (5,31) (5,32)
(5,32) (5,33)
(5,33) (5,34)
(5,34) задається таблицею істинності (табл. 5.5).
задається таблицею істинності (табл. 5.5).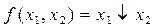
 (5,35)
(5,35) (5,36)
(5,36)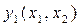
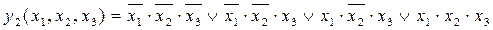 (5,37)
(5,37)
 (5,38)
(5,38) (5,39)
(5,39) (5,40)
(5,40)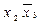





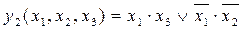 (5,41)
(5,41)


