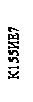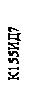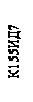Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методічні вказівки до лабораторних робітСодержание книги
Поиск на нашем сайте
МЕТОДІЧНІ ВКАЗІВКИ ДО ЛАБОРАТОРНИХ РОБІТ з курсу за тематикою «Цифрова електроніка» (для студентів напрямку підготовки 0507 «Електромеханіка» II - III курсу всіх форм навчання)
Рекомендовано на засіданні кафедри АЕМС Протокол № від
Затверджено на заседании методради ДонДТУ Протокол № від
Алчевськ ДонДТУ УДК 62-83
Методичні вказівки до лабораторного практикуму з курсу «Електроніка та мікропроцесорна техніка» за тематикою «Цифрова електроніка» для студентів напрямку підготовки 0507 «Електромеханіка»
Наведені теоретичні відомості та методика виконання лабораторних робіт на лабораторному стенді виконаному на мікросхемах ТТЛ структури малого та середнього ступеня інтеграції. Наведена методика побудови табличного та формульного опису цифрових та логічних елементів за результатами експерименту, а також створення часових діаграм для схем послідовного типу.
Укладачі: В.П. Яблонь, доц. В.М. Столяров, доц.
Відповідальний за випуск О.І. Мотченко, проф. Відповідальний редактор В.П. Яблонь, доц. ЗМІСТ 1 ОПИС ЛАБОРАТОРНОГО СТЕНДУ ТА МЕТОДИКИ ЙОГО ВИКОРИСТАННЯ 4 2 ЛАБОРАТОРНА РОБОТА № 1 ДОСЛІДЖЕННЯ РОБОТИ ЛОГІЧНИХ ЕЛЕМЕНТІВ ТА ПРОСТИХ КОМБІНАЦІЙНИХ СХЕМ... 6 3 ЛАБОРАТОРНА РОБОТА № 2 ДОСЛІДЖЕННЯ РОБОТИ КОДУЮЧИХ І ДЕКОДУЮЧИХ ПРИСТРОЇВ 29 4 ЛАБОРАТОРНА РОБОТА № 3 ДОСЛІДЖЕННЯ РОБОТИ ТРИГЕРІВ 39 5 ЛАБОРАТОРНА РОБОТА № 4 ДОСЛІДЖЕННЯ РОБОТИ ЛІЧИЛЬНИКІВ 48 6 ЛАБОРАТОРНА РОБОТА № 5 ДОСЛІДЖЕННЯ РОБОТИ ДІЛЬНИКІВ ЧАСТОТИ 61 ПЕРЕЛІК ПОСИЛАНЬ.. 70 1 ОПИС ЛАБОРАТОРНОГО СТЕНДУ Живлення стенду здійснюється від однофазної мережі змінної напруги 220 B з можливими відхиленнями від номінального значення від Більшість логічних елементів і інтегральних схем зображених на лицьовій панелі стенду забезпечені світлодіодними елементами індикації, за допомогою яких можна судити про логічні вихідні рівні відповідних елементів і схем. При включенні стенду тригерні елементи схем можуть довільно встановитися в будь-який з логічних станів "0" або "1" Тому при включенні стенду в мережу світлодіоди, що відображають вихідні рівні тригерів, спалахують в різних комбінаціях. На всіх виходах елементів з індикацією, стану світлодіода, що світиться, відповідає високий рівень позитивної напруги (рівень логічної одиниці). Виняток становлять тільки мікросхеми DD2 і DD3 дешифраторів, у яких стану виводів при ввімкненій індикації, відповідає низький рівень напруги (рівень логічного нуля). Таке підключення елементів індикації викликане методичними міркуваннями, пов'язаними з наочністю функціонування вказаних мікросхем. Стенд виконаний на мікросхемах ТТЛ структури. У зв'язку з цим, якщо на входи таких мікросхем не подані логічні сигнали (входи не сполучені провідниками з іншими елементами), то це рівносильно подачі на них напруги, що відповідає рівню логічної одиниці. При з'єднанні входів мікросхем з шинами нульового потенціалу стенду слід спочатку штекер сполучного провідника з'єднати з нульовою шиною, а потім другий штекер провідника з'єднати з відповідним входом мікросхеми. Генератор тактових імпульсів стенду (ГТІ) виробляє прямокутні імпульси. При натиснутій кнопці, розташованій в полі умовного позначення ГТІ частота проходження імпульсів генератора складає 1 Гц, при віджатій 100 Кгц. Генератор одиночних імпульсів (ГОІ) при натисненні кнопки, розташованої в полі умовного позначення ГОІ виробляє перепад напруги з 0 в 1, при віджиманні - зворотний перепад з 1 в 0. Елемент затримки (ЕЗ) при натиснутій кнопці, розташованій в полі умовного позначення ЕЗ, здійснює затримку вихідного сигналу ГТІ на 1 мкс. При віджатій кнопці здійснюється затримка вихідного сигналу ГОІ на 1 мкс. У обох випадках форма вихідного сигналу не змінюється. Для підключення осцилографа й зовнішнього генератора стенд укомплектований перехідними вставками, що дозволяють використовувати стандартні кабелі з штекерами діаметром 4 мм.
2 ЛАБОРАТОРНА РОБОТА № 1 Мета лабораторної роботи Метою лабораторної роботи є ознайомлення з основними характеристиками простих логічних елементів, виконаних у вигляді мікросхем; основами синтезу складних логічних елементів і логічних функцій; придбання навичок та умінь перевірки працездатності досліджуваної схеми. Програма лабораторної роботи У програму роботи входить дослідження роботи логічних елементів "І", "АБО", "НЕ", "І-НЕ", "АБО-НЕ", "виключне АБО", а також простих комбінаційних схем відповідно до заданої таблиці істинності. Теоретичні відомості Докладний опис принципу роботи логічних елементів на мікросхемах приведений в [3, 4, 7, 8]. Будь-який цифровий пристрій реалізує деяку логічну функцію. Для того, щоб такий пристрій побудувати, необхідно заздалегідь задати цю функцію в зручному для побудови вигляді. Існує декілька способів завдання логічних функцій. Розглянемо три з них, а саме: словесний, табличний і аналітичний. При словесному способі завдання функція визначається словами, наприклад, якщо будь-які два аргументи дорівнюють 1, то й функція дорівнює 1, у всіх інших випадках функція дорівнює 0. Таблиця істинності, яку складають, користуючись словесним описом, являє собою табличний (матричний) спосіб завдання логічної функції. У таку таблицю включають всі можливі стани вхідних аргументів та відповідні цим станам значення виходу. Аналітичний спосіб полягає в записі логічної функції у вигляді рівняння, яке виходить з таблиці істинності. По логічному рівнянню будують цифрову схему, що реалізовує його. У свою чергу, будь-яку цифрову схему можна побудувати використовуючи логічні елементи. Таким чином, логічні елемент - це електронна схема, яка реалізує певну логічну функцію. Сукупність логічних елементів, призначених для перетворення бінарних змінних, називається логічною схемою. Логічні схеми підрозділяють на комбінаційні та послідовні. Комбінаційною прийнято називати схему з п входами і одним або т виходами, у якої вихідні (вихідний) сигнали в даний момент часу повністю визначаються сукупністю вхідних сигналів, що діють в даний момент часу. Послідовною називають схему, в якій вихідні сигнали в даний момент часу залежать не тільки від станів вхідних сигналів в даний момент часу, але й від їх станів в попередні моменти часу. Послідовні схеми містять в своєму складі елементи пам'яті і різні регістри. При виконанні цієї лабораторної роботи досліджуватимуться комбінаційні логічні схеми. Математичним апаратом для побудови комбінаційних логічних схем є "АЛГЕБРА ЛОГІКИ" або "БУЛЕВА АЛГЕБРА" (по імені англійського математика і логіка Джорджа Буля). Булева алгебра оперує бінарними елементами, тобто елементами які можуть приймати тільки два значення: «0» («Брехня», «False» і тому подібне) і «1» («Істина», «True» і тому подібне). Крім того в алгебрі логіки визначені функції, які описують перетворення бінарних сигналів, тобто перетворення двійкових аргументів цими функціями. У загальному випадку можуть бути визначені Серед цього різноманіття логічних функцій можна виділити елементарні (функції одного або двох аргументів), поєднання яких дозволяє визначити решту всіх можливих функцій. Це випливає з принципу суперпозиції Булевої алгебри, який свідчить, що будь-яку булеву функцію з будь-якою кількістю аргументів можна побудувати через підстановку замість цих аргументів інших функцій. Такими функціями в класичній алгебрі логіки є: «ЗАПЕРЕЧЕННЯ» - функція одного аргументу, «логічне І» і «логічне АБО» - функції двох і більше аргументів. Як буде показано далі одну з двох функцій «логічне І» або «логічне АБО» можна виключити з розгляду і всі операції над аргументами визначати через ту, що залишилася і «ЗАПЕРЕЧЕННЯ». Базові електронні елементи Суперпозиція функцій «ЗАПЕРЕЧЕННЯ» і «логічне І» породжують функцію «І-НЕ» (штрих Шеффера):
А суперпозиція функцій «ЗАПЕРЕЧЕННЯ» і «логічне АБО» породжують функцію «АБО-НЕ» (стрілка Пірса):
Опис елементів «І-НЕ» і «АБО-НЕ» приведено відповідно в таблицях 2.4 і 2.5. Таблиця 2.4 – Логічне «І-НЕ»
Таблиця 2.5 – Логічне «ІЛІ-НЕ»
Кожна з цих функцій може бути базисом для алгебри логіки, тобто через кожну з даних функцій (без використання інших) може бути виражений весь набір всіляких логічних функцій. Ця чудова властивість служить основою для побудови серій логічних мікросхем, зокрема мікропроцесорів і мікроконтролерів. У електроніці це означає, що для реалізації всього різноманіття схем перетворення сигналів, що представляють логічні значення, досить одного або декількох типових елементів. Кожна з серій цифрових мікросхем базується на дискретних електронних елементах, званих базовими. Елемент «І-НЕ», що реалізує функцію Шеффера (штрих Шеффера), використовується при побудові інтегральних мікросхем ТТЛ-структури. Елемент «АБО-НЕ» (стрілка Пірса) використовується в інтегральних мікросхемах к ‑ МОП структури. Використання функцій, що не входять в визначений базис (функціональна надмірність), дозволяє істотно скоротити складність схем, що реалізують логічні вирази, і тим самим підвищити їх надійність. Тому базові елементи служать основою для побудови інших електронних елементів, що реалізують всі необхідні логічні функції. Об'єднуючи на одному кристалі базові елементи отримують мікросхеми, що реалізують функції "І" (конъюнктор), "АБО" (дизъюнктор), "НЕ" (інвертор) та інші. Серії цифрових мікросхем включають велику безліч елементів, що реалізоють як прості та і дуже складні логічні перетворення сигналів. Мінімальність і надмірність - важливі аспекти теорії інформації. Як факт: вимірювання надмірності російської мови дали близько 80%. У сленгах (наприклад, мові авіадиспетчерів) надмірність ще вище. Завершуючи тему базисів слід зазначити, що в «основний» набір електронних логічних елементів і функцій мов програмування зазвичай включають крім кон'юнкції, диз'юнкції, заперечення і ще одну логічну функцію "СУМА ПО МОДУЛЮ 2". Це пояснюється цілою низкою чудових властивостей цієї логічної функції.
Функція «СУМА ПО МОДУЛЮ 2» Логічна функція «СУМА ПО МОДУЛЮ 2» для двох аргументів задається таблицею 2.6. Таблиця 2.6 – Функція «СУМА ПО МОДУЛЮ 2»
Дана функція називається «СУМА ПО МОДУЛЮ 2», тому що обчислюється як залишок від ділення суми своїх аргументів на 2. Перевіримо дане твердження по рядках таблиці 2.6: 1) 2) 3) 4) Таким чином, значення залишків у виразах вище співпадають із значеннями в останньому стовпці таблиці 2.6. Функцію «СУМА ПО МОДУЛЮ 2» ще називають «Виключне АБО», а так само «НЕРІВНОЗНАЧНІСТЬ». Дійсно «1» з'являється в останньому стовпці таблиці 2.6 при неспівпаданні аргументів Неоднозначність технічних і навіть логічних термінів йде від неоднозначності розмовної мови. Наприклад, в граматиці російської мови (та й англійської також) не розрізняються «Виключає АБО» і просто «АБО». Так, у фразі «сніг чи вітер...» союз «чи» (коротка форма «або») має значення диз'юнкції, а у вітанні «гаманець чи життя» (як і в напутті «зі щитом чи на щиті»), той же союз виражає вже «виключне АБО». Насправді, функції «виключне АБО», «НЕРІВНОЗНАЧНІСТЬ» і «СУМА ПО МОДУЛЮ 2» - різні функції, ідентичні тільки у разі двох аргументів. Таблиця 2.7 представляє ці функції для випадку трьох аргументів. Таблиця 2.7 – Тернарні функції «СУМА ПО МОДУЛЮ 2»,
Включення функції «СУМА ПО МОДУЛЮ 2» в набір «популярні» викликано її чудовими властивостями. По-перше, при інвертуванні одного з аргументів ця функція також інвертується. По-друге, ця функція показує, коли аргументи не рівні (а при інвертуванні одного з аргументів - коли рівні). По-третє, вона дозволяє проводити кероване інвертування: при нульовому аргументі інший аргумент не міняється, при одиничному ж значенні другий аргумент інвертується. Нарешті, повторне застосування цієї функції повертає до початкового значення аргументу: якщо У графіці ця функція застосовується при виведенні спрайту на картинку - повторне її застосування прибирає спрайт з картинки. Також ця функція використовується в криптографії - одна з схем шифрування полягає в накладенні якогось коду на потік даних через функцію «СУМА ПО МОДУЛЮ 2». Зашифрований таким чином потік на початковий потік не схожий, але може бути легко відновлений повторним застосуванням шифруючого коду.
Підготовка до роботи 2.4.2.1 Вивчити основи алгебри логіки і роботу логічних елементів, що реалізовують функції однієї і двох змінних (інверсія, повторення, «І», «АБО», «НЕ», «І-НЕ», «АБО‑НЕ», «СУМА ПО МОДУЛЮ 2» й ін.). Для кожної з функцій скласти таблицю істинності, логічне рівняння, привести умовне графічне позначення відповідного елементу. 2.4.2.2 По таблиці істинності функції «СУМА ПО МОДУЛЮ 2» скласти рівняння в ДДНФ і в базисі «І-НЕ». Розробити принципову схему, що реалізовує дану функцію на елементах лабораторного стенду. 2.4.2.3 Відповідно до варіанту (номер бригади) за таблицею 2.11 скласти логічне рівняння заданої логічної функції, мінімізувати його і розробити комбінаційну схему автомата на логічних елементах «І‑НЕ».
Таблиця 2.11 - Таблиця істинності логічного автомата
Проведення досліджень 2.4.3.1 З елементів, що є на стенді, зібрати по черзі схеми, приведені на рисунку 2.3. Подати на входи зібраних логічних схем вхідні рівні напруги («0» і «1») і по вихідній напрузі побудувати таблиці істинності. Порівняти їх з таблицями істинності, отриманими при підготовці до проведення роботи. Визначити яким логічним функціям дані схеми відповідають.
2.4.3.2 Побудувати таблицю істинності чотирьохвходового елементу DD10 і відповідне функціям елементу логічне рівняння. З логічних елементів, що є на стенді, скласти і зібрати схему логічного елементу, що виконує такі ж функції, як і елемент DD10. 2.4.3.2 З логічних елементів, що є на стенді, зібрати схему логічного елементу «СУМА ПО МОДУЛЮ 2» (схема повинна бути отримана в ході домашньої підготовки до лабораторної роботи, див. підпункт 2.4.2.2) 2.4.3.2 Зібрати комбінаційну схему логічного автомата, принципова схема якого отримана в ході підготовки за підпунктом 2.4.2.3. Подати на входи зібраної схеми відповідні вхідні сигнали і переконатися в правильності її роботи. Зміст звіту У звіті повинні бути представлені схеми і умовні позначень досліджуваних логічних елементів і таблиць станів, що ілюструють їх роботу, зміряні параметри, висновок про результати досліджень.
3 ЛАБОРАТОРНА РОБОТА № 2 Мета лабораторної роботи Вивчення принципів роботи, методів синтезу кодуючих і декодуючих пристроїв, виконаних на основі інтегральних мікросхем, придбання навиків і умінь побудови і перевірки працездатності досліджуваних схем. Теоретичні відомості Принципи роботи і методи синтезу кодуючих і декодуючих пристроїв (шифраторів і дешифраторів) приведені в книгах [4, 7, 8]. Кодерами (шифраторами) і декодерами (дешифраторами) називаються пристрою для перетворення вхідних кодів у вихідні. Найчастіше використовуються двійкові кодери і декодери. Шифратори (кодери) Двійкові шифратори перетворять код «1 з N» в двійковий код. При подачі рівня логічної одиниці на один з N входів кодера на його виходах формується двійковий код, що відображає номер цього входу. (на інших входах шифратора при цьому є рівень логічного нуля). Існують шифратори, у яких на один з входів подається рівень логічного нуля, на решті входів шифратора при цьому підтримується рівень логічної одиниці. Одне з основних застосувань шифратора - введення даних з клавіатури, при якому натиснення клавіші з десятковою цифрою повинне приводити до передачі в пристрій двійкового коду даної цифри. Повний шифратор має N входів і n виходів. Причому N=2n. Розглянемо приклад побудови двійкового шифратора для вхідного коду «1 з 3». Таблиця 3.1 є таблицею істинності такого кодера. У початковому «незбудженому» стані входи F1, F2, F3 знаходяться в стані логічного нуля. При подачі на один з входів рівня логічне одиниці на виходах а0, а1 з'явиться двійковий код відповідний десятковому номеру «збудженого» входу.
Таблиця 3.1 – Таблиця істинності шифратора (кодера)
Використовуючи таблицю 3.1 рівнянь кодера можна представити в наступному вигляді:
У базисі «І-НЕ» вирази (3.1) приймають вигляд:
Враховуючи, що даний кодер має три вхідні сигнали, його таблиця істинності має в загальному випадку Проте, в реальних електронних пристроях такі комбінації можуть зустрічатися. Наприклад, при перетворенні номера натиснутої клавіші в двійковий код, можуть зустрітися ситуації коли одночасно натиснутими виявляються декілька клавіш. При побудові цифрового автомата (шифратора) за виразами (3.1) або (3.2) таким ситуаціям відповідатиме «нульовий» сигнал на обох виходах. У ситуаціях коли заборонені комбінації на входах шифратора принципово неможливі, вирази, що описують роботу кодера, можуть бути приведені до простішого вигляду:
У виразах (3.3) «нульові» вхідні сигнали не використовуються, оскільки в коді «1 з N» передбачається, що за наявності одного «одиничного» входу усі інші свідомо «нульові». На підставі отриманих виразів (3.3) будується кодер, показаний на рисунку 3.1.
Аналогічно розглянутому вище будуються кодери (шифратори) з будь-якою кількістю входів.
Дешифратори (декодери) Двійковим дешифратором називається цифровий логічний пристрій, що перетворює двійковий вхідний код у вихідний код «1 з N». Кожному значенню двійкового коду на входах декодера відповідає рівень логічної одиниці на одному з N виходів, номер якого відповідає даному двійковому коду. На решті виходів дешифратора є рівень логічного нуля. Існують дешифратори, де на «вибраному» виході є рівень логічного нуля, а на решті виходів рівень логічної одиниці. Повний декодер має n входів і N виходів, причому N=2n. Дешифратори використовують, як правило, для перетворення двійкового коду числа в сигнал (0 або 1), що управляє, на відповідній шині управління тими або іншими пристроями. Таблиця 3.2 є таблицею істинності двійкового декодера на 2 входи. Таблиця 3.2 – Таблиця істинності дешифратора на два входи
Кожній двійковій комбінації на входах a0, a1 відповідає рівень логічної одиниці на одному з виходів F0 F3. Логічні рівняння виходів декодера мають вигляд:
На основі отриманих рівнянь будується схема декодера, приведена на рисунку 3.2.
Аналогічно будуються декодери на більшу кількість вхідних двійкових розрядів. У лабораторному стенді використовуються інтегральні дешифратори К155ИД7 (див. рисунок 3.3). Вхідний трьохрозрядний двійковий код поступає на входи А0 А2. Декодер має 8 виходів.
Особливість декодера К155ИД7: початковий стан всіх виходів декодера – «1». Кожному вхідному двійковому коду відповідає рівень логічного нуля на одному з восьми виходів декодера, на решті виходів при цьому присутній рівень логічної одиниці. Таким чином на виході дешифраторів К155ИД7 утворюється інверсний код «1 з 8». Входи E0 Е2 дозволяють роботу декодера. Перший вхід Е0 прямої дії, а два нижні входи E1 і Е2 – інверсної дії. Тобто для активізації функцій дешифратора К155ИД7 на вхід дозволу Е0 подається рівень логічної одиниці, а на входи Е1 і Е2 подається рівень логічного нуля. При інших комбінаціях рівнів на цих входах напруга на всіх виходах дешифратора відповідає рівню логічної одиниці (дешифратор не активний). На рисунку 3.3 приведена схема паралельної роботи двох декодерів, а на рисунку 3.4 часові діаграми цієї схеми.
Принцип роботи схеми: перші 7 вхідних комбінацій декодуються декодером DD2, робота декодера DD3 при цьому заборонена по входу дозволу Е0. Після приходу восьмого імпульсу робота декодера DD2 забороняється за инверсними керуючими входами Е1 і Е2, а робота декодера DD3 дозволяється за прямим входом Е0. Таким чином, три перші вхідні сигнали дешифраторів подключені паралельно, а четвертий служить для активації першого (DD2) або другого (DD3) дешифратора. 3.4 Завдання, порядок виконання роботи і проведення Підготовка до роботи 3.4.1.1 Вивчити принципи роботи і методи синтезу кодуючих і декодуючих пристроїв, виконаних на основі інтегральних мікросхем. 3.4.1.2 Вивчити довідкові дані інтегральних кодерів і декодерів ТТЛ і К-МОП структури. Вивчити схеми використання декодерев з різними елементами відображення цифрової і буквеної інформації (цифрові неонові індикатори, світлодіоди і світлодіодні матриці, вакуумні люмінесцентні рідкокристалічні індикатори). Привести умовний графічний опис, таблицю істинності, опис роботи. 3.4.1.3 Скласти таблицю істинності, логічне рівняння і схему шифратора для вхідного коду «1 з 3» на елементах «І-НЕ». 3.4.1.4 Скласти таблицю істинності, логічне рівняння і схему дешифратора на 2 двійкових входа. 3.4.1.5 Вивчити паспортні дані інтегрального декодера К155ИД7, скласти схему паралельної роботи двох декодерів і побудувати діаграму роботи цієї схеми. 3.4.1.6 Скласти схему керування роботою двох декодерів, використовувану при необхідності збільшення кількості декодованих вхідних двійкових розрядів. Проведення досліджень 3.4.2.1 З елементів, що є на стенді, зібрати схему кодера для вхідного коду «1 з 3» на елементах "І-НЕ" і перевірити правильність її функціонування. 3.4.2.2 З елементів, що є на стенді, зібрати схему дешифратора для двійкового коду на два входи на елементах "І-НЕ" і перевірити правильність її функціонування. 3.4.2.3 Зібрати схему паралельної роботи двох декодерів, що є на стенді, і побудувати таблицю істинності. У таблиці істинності врахувати керуючі сигнали Е0 Е2. 3.4.2.4 Зібрати схему керування роботою двох декодерів К155ИД7 при декодуванні 4-х розрядного двійкового коду. Зняти й побудувати часові діаграми роботи вказаної схеми. Зміст звіту У звіті повинні бути представлені умовні позначення кодерів і декодерів, досліджувані схеми, зміряні параметри, часові діаграми, що ілюструють їх роботу, висновок про результати досліджень.
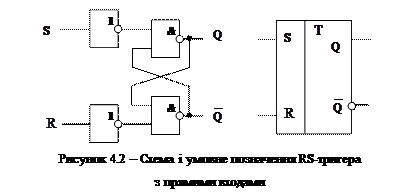
4 ЛАБОРАТОРНА РОБОТА № 3 Мета лабораторної роботи Вивчення принципів роботи, методу синтезу тригерів, виконаних на основі інтегральних мікросхем малого і середнього ступеня інтеграції, придбання навиків і умінь настройки і перевірки працездатності досліджуваних схем. Теоретичні відомості Цифрові функціональні вузли, які містять елементи пам'яті (тригери), отримали назву вузлів послідовного типу. До них відносять: тригери, лічильники, дільники, розподілювачі імпульсів. Ці функціональні вузли входять до складу багатьох серій ІМС. Тригери складають основу багатьох електронних схем. Від функціональних можливостей тригерів та режимів керування ними залежать характеристики регістрів, лічильників та інших вузлів. У сучасних серіях ІМС, тригери подані достатньо широко та різноманітно: одноступінчаті та двоступінчаті, асинхронні та синхронні, з лічильним входом та універсальні за застосуванням, із статичним та динамічним керуванням. На відміну від пристроїв комбінаційного типу, що описуються таблицями істинності, закони функціонування тригерів описуються таблицями станів. У таблиці станів в якості вхідних змінних подають, окрім вхідних аргументів, також і попередні значення виходів. Теоретичні відомості про тригери приведені в літературі [1÷7]. Далі приведені умовні позначення тригерів і схеми для їх реалізації на логічних елементах «І-НЕ». RS-тригер з прямими входами На рисунку 4.2 зображений RS-триггер з прямими входами. Стан входів в режимі зберігання - рівні логічного нуля. Керуючі інформаційні сигнали повинні мати рівень логічної одиниці. В основному робота даного тригера подібна до роботи RS-триггера з інверсними входами. Таблиця 4.2 є таблицею станів тригера з прямими входами.
Таблиця 4.2 – Таблиця станів RS-триггера з прямими входами
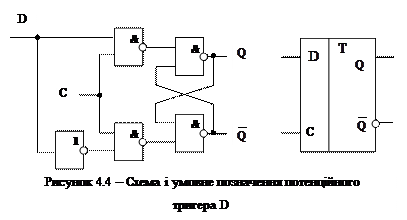
Потенційний D-тригер На рисунку 4.4 зображена схема потенційного D-тригера. Інформація, подана на вхід D (логічний нуль або логічна одиниця), буде записана в тригер після подачі рівня (потенціалу) логічної одиниці на вхід С.
Підготовка до роботи 4.4.1.1 Вивчити роботу тригерів на логічних елементах (RS-триггер з інверсними входами, RS-триггер з прямими входами, тактований RS-триггер, потенційний D-триггер). Користуючись довідником з інтегральних мікросхем [16], проставити номери виводів мікросхем на складених схемах тригерів. Зобразити часові діаграми роботи тригерів і скласти відповідні ним таблиці станів. 4.4.1.2 Дослідити роботу тригерів на мікросхемах середнього ступеня інтеграції (D-триггер, рахунковий тригер на основі D тригера, R-S тригер на основі D-триггера). Користуючись довідником [16], накреслити їх схеми, умовні позначення і таблиці станів. Зобразити часові діаграми роботи тригерів відповідно до таблиць станів.
Проведення досліджень 4.4.2.1 Зібрати по черзі схеми тригерів на логічних елементах (RS-триггер з інверсними входами, RS -триггер з прямими входами, тактований RS-триггер, потенційний D-триггер). Подати на їх входи відповідні керуючі та інформаційні сигнали. За наслідками досліджень замалювати отримані часові діаграми і порівняти їх з раніше складеними при підготовці до роботи. 4.4.2.2 Зібрати по черзі схеми тригерів на мікросхемах середнього ступеня інтеграції (D-триггер, рахунковий тригер на основі D-тригера, R-S тригер на основі D-триггера). Подати на входи тригерів відповідні керуючі та інформаційні сигнали. За наслідками досліджень замалювати отримані часові діаграми і порівняти їх з раніше складеними при підготовці до роботи. Зміст звіту У звіті повинні бути представлені схеми і умовні позначення досліджуваних схем тригерів, часові діаграми і таблиці станів, що ілюструють їх роботу, зміряні параметри, висновок про результати досліджень. 5 ЛАБОРАТОРНА РОБОТА № 4 Мета лабораторної роботи Вивчення принципів роботи, методів синтезу лічильників, виконаних на основі інтегральних мікросхем малого і середнього ступеня інтеграції, придбання навиків і умінь, побудови і перевірки працездатності досліджуваних схем. Теоретичні відомості Циф |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.86.134 (0.014 с.) |

 до + 22 В частоти 50 Гц. Кнопка " МЕРЕЖА" з фіксацією для включення мережевої напруги знаходиться у верхньому лівому куті лицьової панелі стенду. При включенні стенду поряд з кнопкою включення спалахує світлодіод. Для виключення стенду кнопку " МЕРЕЖА" слід вимкнути повторним натисненням.
до + 22 В частоти 50 Гц. Кнопка " МЕРЕЖА" з фіксацією для включення мережевої напруги знаходиться у верхньому лівому куті лицьової панелі стенду. При включенні стенду поряд з кнопкою включення спалахує світлодіод. Для виключення стенду кнопку " МЕРЕЖА" слід вимкнути повторним натисненням.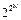 логічних функцій, де
логічних функцій, де 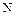 - кількість аргументів функції (враховуючи бінарний характер аргументів отримуємо
- кількість аргументів функції (враховуючи бінарний характер аргументів отримуємо  їх комбінацій, а враховуючи що кожна комбінація дає у відповіді або «0» або «1» отримуємо кількість можливих функцій рівним
їх комбінацій, а враховуючи що кожна комбінація дає у відповіді або «0» або «1» отримуємо кількість можливих функцій рівним  (2.13)
(2.13) (2.14)
(2.14)











 ;
; ;
; ;
; .
.
 , то
, то  і
і  .
.
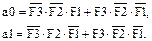 (3.1)
(3.1) (3.2)
(3.2) рядків. Як видно з таблиці 3.1 код «1 з 3» (як і будь-який код «1 з N») є «надмірним» в сенсі кількості використаних вхідних розрядів. Комбінації в яких більш за один вхідний розряд мають значення «Логічна 1» є для коду «1 з N» забороненими.
рядків. Як видно з таблиці 3.1 код «1 з 3» (як і будь-який код «1 з N») є «надмірним» в сенсі кількості використаних вхідних розрядів. Комбінації в яких більш за один вхідний розряд мають значення «Логічна 1» є для коду «1 з N» забороненими. (3.3)
(3.3)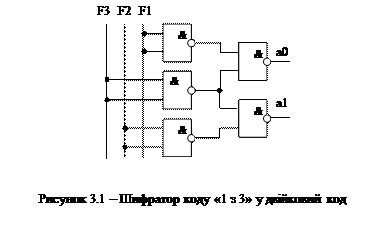
 (3.4)
(3.4)