
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множення і ділення раціональних чиселСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
1. –8 · (–3) = … а) –24; б) 24; в) –11; г) 11. 2. 4 · (–7) = … а) 28; б) –28; в) – 3. –12 · 3 = … а) –36; б) 36; в) –4; г) 4. 4. а) 1; б) –1; в) 0; г) 5. –20: 4 = … а) –80; б) 80; в) 5; г) –5. 6. 130: (–13) = … а) 10; б) –10; в) 1690; г) –1690. 7. –0,6: (–2) = … а) 3; б) –3; в) –0,3; г) 0,3. 8. –13: (–13) = … а) 1; б) –1; в) 169; г) –169.
9. 5 · (–12) · а) 10. 3 · (– a – 2) = … а) –3 a – 2; б) –3 a – 6; в) – a – 6; г) 3 a + 6. 11. –4 · (a – 3) = … а) –4 a + 12; б) –4 a – 12; в) 4 a + 12; г) 4 a – 3.
1. Обчислити: а) –8 · 16; б) 12 · (–10); в) –7 · (–8). 2. Обчислити: а) (–2)4; б) (–3)3. 3. Обчислити: а) –400: 8; б) 60: (–12); в) –102: (–10). 4. Розкрити дужки і звести подібні доданки: 2 · (5 x – 6) – 3 · (2 x – 4). 5. Розв’язати рівняння: а) x · 0,2 = –4,8; б) –68: x = –17.
6. Обчислити значення виразу (–360): (–4) + 8 · (–9). 7. Винести за дужки спільний множник: 18 a + 12 b. 8. Знайти добуток усіх цілих чисел, що задовольняють нерівність
1. Обчислити: а) 2. Обчислити: а) 3. Розкрити дужки і звести подібні доданки: 7(a – 5 b + 3) – 5(a – 7 b – 2). 4. Розв’язати рівняння (x + 2): (–14) = –9.
5. Розкрити дужки і звести подібні доданки: 6. Спростити і обчислити значення виразу 7 · (0,2 x + 3) – 6 · (0,1 x + 2), якщо x = –5. 7. Винести за дужки спільний множник: 56 ab – 32 ac.
1. Спростити вираз 2. Розв’язати рівняння 3. Довести, що a · b = (a: c) · (b · c). 4. Розв’язати рівняння |4 x – 1| = 9.
5. Довести, що добуток усіх цілих відмінних від нуля розв’язків нерівності | x | < 204 є від’ємним числом.
1. –4 · (–3) = … а) 12; б) –12; в) –7; г) 7. 2. 8 · (–6) = … а) 3. –5 · 7 = … а) –2; б) 35; в) –30; г) –35. 4. а) 5. –80: 8 = … а) 10; б) –10; в) –1; г) 160. 6. 81: (–9) = … а) –9; б) 9; в) –2; г) 2. 7. –0,8: (–4) = … а) 2; б) –2; в) 0,2; г) –0,2. 8. –14: (–14) = … а) –1; б) 256; в) –256; г) 1.
9. а) 10. 4 · (–3 – b) = … а) –12 + 4 b; б) 12 – 4 b; в) –12 – 4 b; г) –12 – b. 11. –6 · (a – 8) = … а) –6 a – 8; б) –6 a + 8; в) –6 a – 48; г) –6 a + 48.
1. Обчислити: а) –10 · 15; б) 4 · (–13); в) –9 · (–11). 2. Обчислити: а) (–3)4; б) (–2)5. 3. Обчислити: а) –1000: 8; б) 70: (–15); в) –125: (–10). 4. Розкрити дужки і звести подібні доданки: 3 · (6 – 4 x) – 6 · (5 x + 3). 5. Розв’язати рівняння: а) –0,7 · x = 10,5; б) –448: x = –4.
6. Обчислити значення виразу 3 · (–12) – 420: 7. 7. Винести за дужки спільний множник: 16 a + 14 b. 8. Знайти добуток усіх цілих чисел, що задовольняють нерівність
1. Обчислити: а) 2. Обчислити: а) 3. Розкрити дужки і звести подібні доданки: 8(2 a – 3 b + 1) – 4. Розв’язати рівняння (3 + x): (–12) = –7.
5. Розкрити дужки і звести подібні доданки: 6. Спростити і обчислити значення виразу 9 · (4 – 0,3 x) – 5 · (0,1 x + 6), якщо x = –2. 7. Винести за дужки спільний множник: 84 ad – 56 cd.
1. Спростити вираз 2. Розв’язати рівняння 3. Довести, що a: b = (a · m): (b · m). 4. Розв’язати рівняння |2 x + 1| = 3.
5. Довести, що добуток усіх цілих відмінних від нуля розв’язків нерівності | x | < 101 є додатним числом.
1. –8 · (–4) = … а) –12; б) 12; в) 32; г) –32. 2. 5 · (–3) = … а) –8; б) 8; в) 15; г) –15. 3. –2 · 12 = … а) –24; б) 24; в) 22; г) 14. 4. а) 1; б) –1; в) 5. –36: 2 = … а) –13; б) 18; в) –18; г) –72. 6. 120: (–4) = … а) –30; б) –3; в) –480; г) –40. 7. –0,15: (–3) = … а) –0,5; б) 0,5; в) 0,05; г) –0,05. 8. –18: (–18) = … а) –18; б) 1; в) –1; г) 18.
9. а) 10. 6 · (– a – 3) = … а) 6 a – 3; б) 6 a + 3; в) –6 a – 3; г) –6 a – 18. 11. 7 · (a – 5) = … а) 7 a – 5; б) 7 a – 35; в) a – 35; г) –7 a + 35.
1. Обчислити: а) –12 · 9; б) 13 · (–10); в) –8 · (–9). 2. Обчислити: а) (–4)2; б) (–5)3. 3. Обчислити: а) –800: 20; б) 72: (–12); в) –305: (–10). 4. Розкрити дужки і звести подібні доданки: 10 · (3 x – 2) – 4 · (–5 + 2 x). 5. Розв’язати рівняння: а) x · 1,9 = –15,2; б) –256: x = –8.
6. Обчислити значення виразу –120: (–3) + 11 · (–3). 7. Винести за дужки спільний множник: 26 a + 13 b. 8. Знайти добуток усіх цілих чисел, що задовольняють нерівність
1. Обчислити: а) 2. Обчислити: а) 3. Розкрити дужки і звести подібні доданки: 9(7 a – 4 b – 3) – 4. Розв’язати рівняння (x – 4): (–13) = 4.
5. Розкрити дужки і звести подібні доданки: 6. Спростити і обчислити значення виразу 0,3 · (3 x – 4) – 5 · (0,2 x – 1), якщо x = –0,86. 7. Винести за дужки спільний множник: 102 xy – 85 yz.
1. Спростити вираз 2. Розв’язати рівняння 3. Довести, що a: b = (a: m): (b: m). 4. Розв’язати рівняння |2 x – 1| = 3.
5. Довести, що добуток усіх цілих відмінних від нуля розв’язків нерівності | x | < 99 є додатним числом.
1. –10 · (–2) = … а) –5; б) 5; в) –20; г) 20. 2. 9 · (–3) = … а) –27; б) 27; в) –3; г) 3. 3. –6 · 7 = … а) 42; б) –42; в) 4. а) –1; б) 1; в) 5. –45: 9 = … а) 5; б) –5; в) 6. 100: (–25) = … а) –5; б) 4; в) –4; г) 7. –0,3: (–3) = … а) 1; б) –1; в) –0,1; г) 0,1. 8. –17: (–17) = … а) –17; б) 17; в) 1; г) –1.
9. а) 10. 8 · (– x – 4) = … а) –8 x – 32; б) –8 x – 4; в) 8 x + 4; г) –8 x + 4. 11. –3 · (x – 9) = … а) –3 x – 9; б) –3 x – 27; в) –3 x + 27; г) 3 x – 9.
1. Обчислити: а) –13 · 3; б) 15 · (–4); в) –11 · (–9). 2. Обчислити: а) (–5)2; б) (–4)3. 3. Обчислити: а) –240: 12; б) 102: (–3); в) –256: (–10). 4. Розкрити дужки і звести подібні доданки: (6 x – 7) · 4 – 2 · (12 x – 5). 5. Розв’язати рівняння: а) –49,5 · x = 5; б) –192: x = –4.
6. Обчислити значення виразу –480: (–40) + 4 · (–13). 7. Винести за дужки спільний множник: 28 b – 14 a. 8. Знайти добуток усіх цілих чисел, що задовольняють нерівність
1. Обчислити: а) 2. Обчислити: а) 3. Розкрити дужки і звести подібні доданки: 7(8 a – 3 b + 4) – 4. Розв’язати рівняння (20 – x): 8 = –13.
5. Розкрити дужки і звести подібні доданки: 6. Спростити і обчислити значення виразу 0,7 · (0,2 c – 9) – 4 · (0,25 c – 3), якщо c = –3. 7. Винести за дужки спільний множник: 72 bc – 108 ac.
1. Спростити вираз 2. Розв’язати рівняння 3. Довести, що a · b = (a · c) · (b: c). 4. Розв’язати рівняння |3 x – 1| = 5.
5. Довести, що добуток усіх цілих відмінних від нуля розв’язків нерівності | x | < 100 є від’ємним числом.
1. –5 · (–12) = … а) –60; б) 60; в) –50; г) 17. 2. 8 · (–4) = … а) –32; б) 32; в) –12; г) 12. 3. –3 · 11 = … а) 33; б) –14; в) 14; г) –33. 4. а) 5. –35: 7 = … а) 6. 100: (–4) = … а) –25; б) –20; в) 25; г) 20. 7. –0,9: (–3) = … а) –0,3; б) 0,3; в) –3; г) 3. 8. –40: (–40) = … а) –40; б) 40; в) –1; г) 1.
9. а) 10. 5 · (– y – 4) = … а) –5 y – 4; б) –5 y – 20; в) –5 y + 20; г) – y – 20. 11. –7 · (y – 2) = … а) –7 y + 14; б) –7 y – 14; в) –7 y – 2; г) 7 y + 2.
1. Обчислити: а) –8 · 12; б) 6 · (–13); в) –6 · (–8). 2. Обчислити: а) (–10)3; б) (–4)4. 3. Обчислити: а) –840: 2; б) 225: (–3); в) –201: (–10). 4. Розкрити дужки і звести подібні доданки: 2 · (15 x – 4) – 6 · (10 x – 3). 5. Розв’язати рівняння: а) x · (–0,6) = 9,6; б) –84: x = –21.
6. Обчислити значення виразу –9 · 6 + (–180): (–9). 7. Винести за дужки спільний множник: 28 a – 14 b. 8. Знайти добуток усіх цілих чисел, що задовольняють нерівність
1. Обчислити: а) 2. Обчислити: а) 3. Розкрити дужки і звести подібні доданки: 8(2 a – 7 b – 3) – 4. Розв’язати рівняння (x – 13): (–8) = –4.
5. Розкрити дужки і звести подібні доданки: 6. Спростити і обчислити значення виразу –9 · (0,3 x – 8) + 4 · (11 x – 2), якщо x = –0,2. 7. Винести за дужки спільний множник: 96 mn – 120 np.
1. Спростити вираз 2. Розв’язати рівняння 3. Довести, що a: с + b: c = (a + b): c. 4. Розв’язати рівняння |2 x + 5| = 3.
5. Довести, що добуток усіх цілих відмінних від нуля розв’язків нерівності | x | < 1000 є від’ємним числом.
1. –9 · (–3) = … а) 3; б) –3; в) –27; г) 27. 2. 4 · (–8) = … а) –2; б) 32; в) 2; г) –32. 3. –5 · 6 = … а) –30; б) 30; в) 4. а) 1; б) –1; в) 5. –27: 3 = … а) 9; б) 6. 140: (–7) = … а) 2; б) 20; в) –2; г) –20. 7. –0,12: (–3) = … а) 0,4; б) –0,4; в) –0,04; г) 0,04. 8. –41: (–41) = … а) –41; б) 1; в) 41; г) –1.
9. а) 2; б) 10. 4 · (–5 – x) = … а) –20 – 4 x; б) –20 – x; в) 20 – 4 x; г) 20 + 4 x. 11. –7 · (x – 9) = … а) –7 x – 9; б) –7 x + 63; в) 7 x + 63; г) –7 x – 63.
1. Обчислити: а) –22 · 4; б) 8 · (–11); в) –5 · (–15). 2. Обчислити: а) (–10)4; б) (–3)5. 3. Обчислити: а) –640: 8; б) 143: (–13); в) –105: (–10). 4. Розкрити дужки і звести подібні доданки: 16 · (2 x – 3) – 4 · (8 x – 9). 5. Розв’язати рівняння: а) –0,7 · x = 24,5; б) –192: x = –4.
6. Обчислити значення виразу –720: (–80) + 3 · (–5). 7. Винести за дужки спільний множник: 100 b – 25 a. 8. Знайти добуток усіх цілих чисел, що задовольняють нерівність
1. Обчислити: а) 2. Обчислити: а) 3. Розкрити дужки і звести подібні доданки: 4(25 a – 3 b – 1) – 4. Розв’язати рівняння (56 – x): (–12) = –6.
5. Розкрити дужки і звести подібні доданки: 6. Спростити і обчислити значення виразу (5 x – 0,1) · 1,6 – 4 · (1,8 x – 3), якщо x = –4,5. 7. Винести за дужки спільний множник: 42 xy – 168 yz.
1. Спростити вираз 2. Розв’язати рівняння 3. Довести, що a: c – b: c = (a – b): c. 4. Розв’язати рівняння |8 + 3 x | = 1.
5. Довести, що добуток усіх цілих відмінних від нуля розв’язків нерівності | x | < 1001 є додатним числом.
РІВНЯННЯ
1. Яке з наведених чисел є коренем рівняння –2 x = 8? а) 2. Корінь рівняння 5 x = –2 дорівнює значенню виразу: а) 5: (–2); б) –2: 5; в) –2 + 5; г) 5 · (–2). 3. Якщо в рівнянні 6 x + 5 = 7 доданок 5 перенести у праву частину, то одержимо рівняння: а) 6 x = 7 + 5; б) 6 x = 7 · 5; в) 6 x = –7 · 5; г) 6 x = 7 – 5. 4. Якщо в рівнянні 5 x = 2 x – 3 доданок 2 x перенести в ліву частину, то одержимо рівняння: а) 5 x – 2 x = –3; б) 5 x – 2 x = 3; в) 5 x + 2 x = 3; г) 5 x + 2 x = –3. 5. Одне з чисел на 4,2 більше, ніж друге. Якщо менше з чисел позначити через x, то більше з чисел буде дорівнювати: а) 4,2 x; б) x + 4,2; в) x – 4,2; г) 4,2 – x. 6. Одне з додатних чисел у 3 рази більше, ніж друге. Якщо менше з чисел позначити через x, то більше число буде дорівнювати: а) x – 3; б) x + 3; в) x: 3; г) 3 x.
1. Розв’язати рівняння: а) –9 x = 5; б) 10 x – 9 = 0. 2. Розв’язати рівняння 7 x – 11 = 13 – x. 3. У двох бригадах працює 96 чоловік, причому у першій — на 12 чоловік більше, ніж у другій. Скільки чоловік у кожній бригаді? Розв’язати задачу за допомогою рівняння. 4. У першому бідоні в 4 рази більше молока, ніж у другому. Скільки молока в першому бідоні, якщо в ньому на 18 л молока більше, ніж у другому? Розв’язати задачу за допомогою рівняння.
5. Поле, площа якого 535 га, розділили на 2 ділянки, одна з яких у 4 рази більша, ніж друга. Знайти площу кожної земельної ділянки.
1. Розв’язати рівняння 2(x – 1,5) + 4 = x – 5. 2. Розв’язати рівняння 3. За три дні туристи пройшли 76 км. За другий день вони пройшли на 6 км більше, ніж за перший, а за третій — на 8 км менше, ніж за другий. Скільки кілометрів проходили туристи кожного дня? 4. Перша друкарка може передрукувати рукопис на 1,5 год раніше, ніж друга. За годину перша друкарка друкує 10 сторінок, а друга — 8 сторінок. За скільки годин може передрукувати даний рукопис перша друкарка?
5. Сума двох чисел дорівнює 105,8. Одне з них на 30% більше, ніж інше. Знайти менше з цих чисел. 6. На першій ділянці у 4 рази більше кущів малини, ніж на другій. Якщо з першої ділянки пересадити на другу 60 кущів, то на обох ділянках кущів стане порівну. Скільки кущів малини було на кожній ділянці спочатку?
1. Розв’язати рівняння 2. У першій бригаді було у 5 разів більше робітників, ніж у другій. Після того як з першої бригади перевели 7 чоловік у другу, у першій стало людей у два рази більше, ніж у другій. Скільки робітників було у кожній бригаді спочатку? 3. 0,7 першого числа дорівнює 0,5 другого числа. Знайти ці числа, якщо їх різниця дорівнює 20. 4. З пункту А в пункт В виїхав пасажирський поїзд швидкість якого 60 км/год. Через 40 хвилин назустріч йому з пункту В виїхав швидкий поїзд зі швидкістю 90 км/год. Відстань між пунктами дорівнює 490 км. Яку відстань проїхав до зустрічі пасажирський поїзд?
5. Розв’язати рівняння 6. З пункту А в пункт В виїхав велосипедист. Через 0,6 год слідом за ним виїхав мотоцикліст, швидкість якого на 20 км/год більша, ніж швидкість велосипедиста. Через 2,4 год після відправлення мотоцикліст проїхав на 36 км більше, ніж велосипедист. Знайти швидкість велосипедиста.
1. Яке з наведених чисел є коренем рівняння –3 x = –12? а) –4; б) 4; в) 2. Корінь рівняння 7 x = –4 дорівнює значенню виразу: а) 7 · (–4); б) 7 + (–4); в) 7: (–4); г) –4: 7. 3. Якщо в рівнянні 3 x + 2 = 11 доданок 2 перенести у праву частину, то одержимо рівняння: а) 3 x = 11 – 2; б) 3 x = 11 + 2; в) 3 x = 11 · 2; г) 3 x = –2 · 11. 4. Якщо в рівнянні 7 x = 3 x – 5 доданок 3 x перенести в ліву частину, то одержимо рівняння: а) 7 x – 3 x = 5; б) 7 x + 3 x = 5; в) 7 x – 3 x = –5; г) 7 x + 3 x = –5. 5. Одне з чисел на 3,6 більше, ніж друге. Якщо менше з чисел позначити через x, то більше з чисел буде дорівнювати: а) x + 3,6; б) x – 3,6; в) 3,6 x; г) x: 3,6. 6. Одне з додатних чисел у 4 рази більше, ніж друге. Якщо менше з чисел позначити через x, то більше число буде дорівнювати: а) x – 4; б) x + 4; в) x: 4; г) 4 x.
1. Розв’язати рівняння: а) –5 x = 4; б) 15 x – 3 = 0. 2. Розв’язати рівняння 8 x + 3 = –11 + x. 3. У гаражі 120 легкових і вантажних автомобілів, причому вантажних на 24 більше, ніж легкових. Скільки вантажних і скільки легкових автомобілів у гаражі? Розв’язати задачу за допомогою рівняння. 4. У першому ящику в 3 рази більше яблук, ніж у другому. Скільки яблук у першому ящику, якщо в ньому на 40 яблук більше, ніж у другому? Розв’язати задачу за допомогою рівняння.
5. У двох зерносховищах 294 т зерна. Скільки тонн зерна у кожному зерносховищі, якщо в першому в 5 разів більше зерна, ніж у другому?
1. Розв’язати рівняння 6(x + 4) + 13 = 4(x – 0,5) – 1. 2. Розв’язати рівняння 3. За три дні зорали 240 га поля. За другий день зорали у 2 рази менше, ніж за перший і на 20 га менше, ніж за третій. Скільки гектарів зорали за другий день? 4. Задану кількість деталей робітник може виготовити на два дні раніше, ніж його учень. За один день робітник виготовляє 15 деталей, а його учень — 10. За скільки днів виготовить задану кількість деталей учень?
5. Периметр прямокутника дорівнює 108 см. Знайти сторони прямокутника, якщо одна з них на 20% менша, ніж друга. 6. На першій полиці книг у 3 рази більше, ніж на другій. Після того як з першої полиці перенесли на другу 24 книги, то на обох полицях книг стало порівну. Скільки книг було на кожній полиці спочатку?
1. Розв’язати рівняння 2. У першій пачці було у 2 рази більше зошитів, ніж у другій. Після того як із другої пачки переклали в першу 10 зошитів, то у другій пачці стало зошитів у чотири рази менше, ніж у першій. Скільки зошитів було в кожній пачці спочатку? 3. Шнурок довжиною 60 м розрізали на дві частини так, що 4. З пункту А в пункт В, відстань між якими 240 км, виїхав мотоцикліст. Через 15 хвилин назустріч йому з пункту В виїхав автомобіль. На якій відстані від пункту А вони зустрінуться, якщо швидкість мотоцикліста становить 50 км/год, а швидкість автомобіля — 80 км/год?
5. Розв’язати рівняння 6. З пункту А в пункт В виїхав автобус. Через 1 год слідом за ним виїхав автомобіль, швидкість якого на 20 км/год більша, ніж швидкість автобуса. Через 2,5 год після відправлення автомобіль проїхав на 10 км більше, ніж автобус. Знайти швидкість автомобіля.
1. Яке з наведених чисел є коренем рівняння 6 x = –18? а) 3; б) –3; в) 2. Корінь рівняння –5 x = 16 дорівнює значенню виразу: а) 16 + (–5); б) 16 – (–5); в) –5: 16; г) 16: (–5). 3. Якщо в рівнянні 4 x + 3 = 15 доданок 3 перенести у праву частину, то одержимо рівняння: а) 4 x = 15 · 3; б) 4 x = 15 + 3; в) 4 x = 15 – 3; г) 4 x = 15: 3. 4. Якщо в рівнянні 19 x = –5 x + 2 доданок –5 x перенести в ліву частину, то одержимо рівняння: а) 19 x + 5 x = 2; б) 19 x – 5 x = 2; в) 19 x + 5 x = –2; г) 19 x – 5 x = –2. 5. Одне з чисел на 5,4 більше, ніж друге. Якщо менше з чисел позначити через x, то більше з чисел буде дорівнювати: а) x – 5,4; б) x + 5,4; в) 5,4 x; г) x: 5,4. 6. Одне з додатних чисел у 7 раз більше, ніж друге. Якщо менше з чисел позначити через x, то більше число буде дорівнювати: а) x – 7; б) x + 7; в) x: 7; г) 7 x.
|

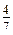 ; г)
; г)  …
… .
. …
…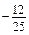 ; б)
; б)  ; в) –12; г) 12.
; в) –12; г) 12. ; б)
; б)  ; в) 2 · (–2,5) · (–4).
; в) 2 · (–2,5) · (–4). ; б) (–30,6): (–0,04); в)
; б) (–30,6): (–0,04); в) 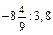 .
. .
. .
. .
. ; б)
; б) 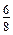 ; в) –48; г) 48.
; в) –48; г) 48.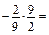 …
… ; б)
; б)  ; в) –1; г) 1.
; в) –1; г) 1.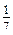 · 2 · (–7) = …
· 2 · (–7) = … ; б)
; б) 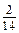 ; в)
; в)  ; г) –2.
; г) –2. ; б)
; б) 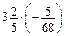 ; в) (–3,5) · 2 · (–0,5).
; в) (–3,5) · 2 · (–0,5). ; б) (–54,6): (–0,06); в)
; б) (–54,6): (–0,06); в)  .
. .
. .
. .
. …
… ; г)
; г)  .
.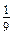 · (–7) · 9 = …
· (–7) · 9 = … ; б)
; б)  ; в) –7; г) 7.
; в) –7; г) 7. ; б)
; б) 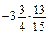 ; в) 0,4 · (–9,7) · (–5).
; в) 0,4 · (–9,7) · (–5). ; б) (–48,8): (–0,4); в)
; б) (–48,8): (–0,4); в)  .
. .
. .
.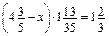 .
.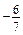 ; г)
; г) 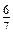 .
. …
…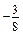 ; г)
; г)  .
.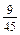 ; г)
; г)  .
. .
.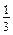 · (–8) · 3 = …
· (–8) · 3 = … ; б) –8; в) 8; г)
; б) –8; в) 8; г) 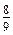 .
. ; б)
; б)  ; в) –0,25 · 8,4 · (–40).
; в) –0,25 · 8,4 · (–40). ; б) (–2,56): (–0,8); в)
; б) (–2,56): (–0,8); в)  .
. .
. .
. .
. …
… ; б)
; б) 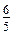 ; в) –1; г) 1.
; в) –1; г) 1. ; б)
; б)  ; в) –5; г) 5.
; в) –5; г) 5. · (–3) ·
· (–3) ·  = …
= … ; б)
; б)  ; в) –3; г) 3.
; в) –3; г) 3. ; б)
; б)  ; в) 0,125 · (–0,63) · (–8).
; в) 0,125 · (–0,63) · (–8). ; б) (–2,59): (–3,7); в)
; б) (–2,59): (–3,7); в)  .
. .
. .
. .
. .
. …
… ; г)
; г)  ; в) –9; г)
; в) –9; г)  .
.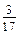 · 2 ·
· 2 ·  = …
= … ; в) –2; г)
; в) –2; г)  .
.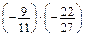 ; б)
; б)  ; в) (–0,8) · 0,7 · (–12,5).
; в) (–0,8) · 0,7 · (–12,5). ; б) (–29,5): (–0,05); в)
; б) (–29,5): (–0,05); в)  .
. .
. .
. .
.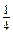 ; б) 4; в) –4; г)
; б) 4; в) –4; г)  .
. .
.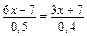 .
. .
. .
. .
. .
. .
.


