
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Додавання і віднімання раціональних чиселСодержание книги Поиск на нашем сайте
1. –3 + (–12) =... а) 15; б) –15; в) –9; г) 9. 2. –8 + 13 =... а) –21; б) 21; в) –5; г) 5. 3. 14 + (–19) =... а) –5; б) –33; в) 33; г) 5. 4. –7 + 7 =... а) 14; б) –14; в) 7; г) 0. 5. 7 – 13 =... а) 6; б) –6; в) –20; г) 20. 6. –24 – 11 =... а) –35; б) –13; в) 13; г) 35. 7. 12 – (–3) =... а) 9; б) –9; в) –15; г) 15. 8. –14 – (–6) =... а) –20; б) 20; в) –8; г) 8.
9. 5 + (–2) + (–5) =... а) 12; б) –12; в) –2; г) 2. 10. 5 + (– a + b) =... а) 5 – a + b; б) 5 + a – b; в) 5 – a – b; г) 5 + a + b. 11. –7 – (–7 + a) =... а) –14 + a; б) –14 – a; в) a; г) – a. 12. Якщо точки А(–3) і В(8) є кінцями відрізка АВ, то довжина цього відрізка дорівнює значенню виразу: а) –3 – 8; б) 8 – (–3); в) 8 + (–3); г) –3 + 8.
1. Обчислити: а) –7 + (–26); б) –45 + 24; в) 37 + (–24). 2. Обчислити: а) 5 – 12; б) –16 – 2; в) 17 – (–4); г) –13 – (–5). 3. Розкрити дужки і спростити вираз: (a – 2,3) – (a – 4,7). 4. Розв’язати рівняння: а) x + 20 = 13; б) 45 – x = –4.
5. Обчислити відстань між точками А(–3) і В(5) координатної прямої. 6. Знайти значення виразу 50 – (–86) – 140.
1. Обчислити: а) 2. Обчислити: а) 3. Розкрити дужки і знайти значення виразу 4. Розв’язати рівняння (x – 3) + 17 = –14.
5. Спростити вираз a + b – (b – 2 c) + (d – 2 c) і знайти його значення, якщо a = 7,8, d = –10,22. 6. Довжина відрізка АВ координатної прямої дорівнює 5. Знайти координату точки В, якщо А(–3). Знайти всі розв’язки задачі. 7. Знайти суму всіх цілих розв’язків нерівності –5 < x < 3.
1. Розкрити дужки і знайти значення виразу 2. Розв’язати рівняння 3. Записати за допомогою букв і довести, що при зменшенні зменшуваного і від’ємника на одне й те саме число різниця не зміниться. 4. Розв’язати рівняння | x | – 4 = –1.
5. Обчислити площу квадрата ABCD, якщо A(–3; 0) і С(4; 0). 6. Довести, що сума всіх цілих розв’язків нерівності | x | < 20 дорівнює 0. 7. Розв’язати рівняння | x + 5| = 11.
1. –11 + (–5) =... а) –16; б) 16; в) 6; г) –6. 2. –12 + 14 =... а) –2; б) –26; в) 2; г) 26. 3. 7 + (–12) =... а) –19; б) 19; в) 5; г) –5. 4. –8 + 8 =... а) –16; б) 16; в) 0; г) 8. 5. 8 – 16 =... а) 8; б) –8; в) 24; г) –24. 6. –13 – 17 =... а) –4; б) 4; в) –30; г) 30. 7. 11 – (–5) =... а) 16; б) 6; в) –6; г) –16. 8. –13 – (–7) =... а) –20; б) 20; в) 6; г) –6.
9. 6 + (–4) + (–6) =... а) –16; б) 16; в) 4; г) –4. 10. 4 + (a – b) =... а) 4 – a – b; б) 4 – a + b; в) 4 + a + b; г) 4 + a – b. 11. –6 – (b – 6) =... а) –12 – b; б) – b; в) –12 + b; г) b. 12. Якщо точки А(–7) і В(12) є кінцями відрізка АВ, то довжина цього відрізка дорівнює значенню виразу: а) –7 – 12; б) 12 – (–7); в) 12 + (–7); г) –7 + 12.
1. Обчислити: а) –12 + (–31); б) –62 + 34; в) 45 + (–16). 2. Обчислити: а) 7 – 24; б) –15 – 6; в) 19 – (–8); г) –11 – (–3). 3. Розкрити дужки і спростити вираз: (b – 1,7) – (b – 3,3). 4. Розв’язати рівняння: а) x + 18 = 10; б) 37 – x = –9.
5. Обчислити відстань між точками А(–8) і В(12) координатної прямої. 6. Знайти значення виразу 25 – (–49) – 104.
1. Обчислити: а) 2. Обчислити: а) 3. Розкрити дужки і знайти значення виразу 4. Розв’язати рівняння (x – 4) + 19 = –16.
5. Спростити вираз 2 a – (c – 3 d) + (–2 a – 3 d) – b і знайти його значення, якщо c = 18,3, b = –4,12. 6. Довжина відрізка CD координатної прямої дорівнює 7. Знайти координату точки D, якщо C(–2). Знайти всі розв’язки задачі. 7. Знайти суму всіх цілих розв’язків нерівності –8 < x < 6.
1. Розкрити дужки і знайти значення виразу 2. Розв’язати рівняння 3. Записати за допомогою букв і довести, що при збільшенні зменшуваного і від’ємника на одне й те саме число різниця не зміниться. 4. Розв’язати рівняння | x | – 3 = –2.
5. Обчислити площу квадрата ABCD, якщо B(–5; 0) і D(–2; 0). 6. Довести, що сума всіх цілих розв’язків нерівності | x | < 15 дорівнює 0. 7. Розв’язати рівняння | x + 4| = 13.
1. –6 + (–13) =... а) –7; б) 7; в) –19; г) 19. 2. –9 + 12 =... а) 3; б) –21; в) 21; г) –3. 3. 6 + (–19) =... а) 13; б) –13; в) –25; г) 25. 4. –5 + 5 =... а) –5; б) –10; в) 10; г) 0. 5. 9 – 14 =... а) 5; б) –5; в) –23; г) 23. 6. –12 – 13 =... а) –25; б) –1; в) 25; г) 1. 7. 13 – (–3) =... а) 10; б) –10; в) –16; г) 16. 8. –12 – (–8) =... а) –20; б) 20; в) –4; г) 4.
9. 4 + (–6) + (–4) =... а) –6; б) 6; в) 14; г) –14. 10. 8 + (– b + a) =... а) 8 + b – a; б) 8 – b – a; в) –8 – b + a; г) 8 – b + a. 11. –7 – (– a – 7) =... а) –14 + a; б) a; в) – a; г) 14 – a. 12. Якщо точки А(–4) і В(9) є кінцями відрізка АВ, то довжина цього відрізка дорівнює значенню виразу: а) –9 – (–4); б) 9 – (–4); в) –4 + 9; г) –4 – 9.
1. Обчислити: а) –9 + (–27); б) –81 + 23; в) 45 + (–24). 2. Обчислити: а) 8 – 36; б) –18 – 8; в) 40 – (–13); г) –16 – (–7). 3. Розкрити дужки і спростити вираз: (a – 3,4) – (a – 9,6). 4. Розв’язати рівняння: а) 15 + x = 7; б) 42 – x = –13.
5. Обчислити відстань між точками А(–4) і В(28) координатної прямої. 6. Знайти значення виразу 43 – (–24) – 150.
1. Обчислити: а) 2. Обчислити: а) 3. Розкрити дужки і знайти значення виразу 4. Розв’язати рівняння (x – 2) + 13 = –11.
5. Спростити вираз b – 2 a – (–2 a + c) – (– c – d) і знайти його значення, якщо b = –12,24, d = –3,8. 6. Довжина відрізка АВ координатної прямої дорівнює 4. Знайти координату точки A, якщо B(1). Знайти всі розв’язки задачі. 7. Знайти суму всіх цілих розв’язків нерівності –9 < x < 7.
1. Розкрити дужки і знайти значення виразу 2. Розв’язати рівняння 3. Записати за допомогою букв і довести, що при одночасному збільшенні одного з доданків і зменшенні другого на одне й те саме число сума не зміниться. 4. Розв’язати рівняння 7 – | x | = –2.
5. Обчислити периметр квадрата ABCD, якщо С(–12; 0) і D(–3; 0). 6. Довести, що сума всіх цілих розв’язків нерівності | x | < 47 дорівнює 0. 7. Розв’язати рівняння |4 – x | = 5.
1. –2 + (–12) =... а) –10; б) 10; в) –14; г) 14. 2. –6 + 15 =... а) –21; б) 9; в) –9; г) 21. 3. –13 + 4 =... а) –9; б) 9; в) –17; г) 17. 4. 9 + (–9) =... а) 0; б) –9; в) –18; г) 18. 5. 10 – 15 =... а) –25; б) –5; в) 5; г) 25. 6. –14 – 8 =... а) –22; б) –6; в) 22; г) 6. 7. 16 – (–6) =... а) 10; б) –10; в) –22; г) 22. 8. –15 – (–3) =... а) –12; б) 12; в) –18; г) 18.
9. 1 + (–9) + (–1) =... а) –7; б) 7; в) –9; г) 9. 10. –5 + (– a + b) =... а) –5 – a – b; б) –5 – a + b; в) 5 – a + b; г) 5 – a – b. 11. –7 – (–7 + a) =... а) a; б) –14 + a; в) –14 – a; г) – a. 12. Якщо точки А(–3) і В(13) є кінцями відрізка АВ, то довжина цього відрізка дорівнює значенню виразу: а) 13 – (–3); б) –3 – 13; в) 13 + (–3); г) –3 + 13.
1. Обчислити: а) –11 + (–26); б) –49 + 13; в) 57 + (–19). 2. Обчислити: а) 19 – 43; б) –29 – 4; в) 60 – (–23); г) –22 – (–4). 3. Розкрити дужки і спростити вираз: (b – 12,6) – (b – 27,4). 4. Розв’язати рівняння: а) 43 + x = 20; б) 21 – x = –2.
5. Обчислити відстань між точками А(–9) і В(13) координатної прямої. 6. Знайти значення виразу 48 – (–18) – 230.
1. Обчислити: а) 2. Обчислити: а) 3. Розкрити дужки і знайти значення виразу 4. Розв’язати рівняння (x – 5) + 26 = –17.
5. Спростити вираз c + d – (–3 a + d) + (–3 a – b) і знайти його значення, якщо c = –40,28, b = 15,4. 6. Довжина відрізка АВ координатної прямої дорівнює 10. Знайти координату точки A, якщо B(2). Знайти всі розв’язки задачі. 7. Знайти суму всіх цілих розв’язків нерівності –6 < x < 4.
1. Розкрити дужки і знайти значення виразу 2. Розв’язати рівняння 3. Записати за допомогою букв і довести властивість: щоб до одного числа додати різницю двох інших чисел, можна до цього числа додати зменшуване і від цієї суми відняти від’ємник. 4. Розв’язати рівняння | x | – 6 = –3.
5. Обчислити периметр рівностороннього трикутника ABC, якщо 6. Довести, що сума всіх цілих розв’язків нерівності | x | < 24 дорівнює 0. 7. Розв’язати рівняння | x – 4| = 15.
1. –4 + (–15) =... а) –19; б) –11; в) 19; г) 11. 2. –4 + 14 =... а) –28; б) –10; в) 10; г) 28. 3. 6 + (–18) =... а) –24; б) –12; в) 12; г) 24. 4. –3 + 3 =... а) –6; б) 6; в) –3; г) 0. 5. 8 – 19 =... а) –11; б) 11; в) –27; г) 27. 6. –17 – 7 =... а) –10; б) 10; в) 24; г) –24. 7. 15 – (–3) =... а) 8; б) 18; в) –18; г) –8. 8. –9 – (–1) =... а) –8; б) –10; в) 8; г) 10.
9. –3 + (–5) + 3 =... а) 5; б) –11; в) –5; г) 1. 10. –4 + (– x + y) =... а) –4 – x + y; б) –4 – x – y; в) –4 + x – y; г) 4 – x + y. 11. –5 – (x – 5) =... а) –10 – x; б) – x; в) x; г) 10 + x. 12. Якщо точки А(–4) і В(18) є кінцями відрізка АВ, то довжина цього відрізка дорівнює значенню виразу: а) –4 + 18; б) 18 – 4; в) 18 – (–4); г) 4 – 18.
1. Обчислити: а) –17 + (–42); б) –58 + 14; в) 62 + (–27). 2. Обчислити: а) 14 – 30; б) –45 – 18; в) 43 – (–18); г) –25 – (–13). 3. Розкрити дужки і спростити вираз: (b – 12,3) – (b – 26,7). 4. Розв’язати рівняння: а) 28 + x = 15; б) 30 – x = –17.
5. Обчислити відстань між точками А(–2) і В(18) координатної прямої. 6. Знайти значення виразу 71 – (–14) – 110.
1. Обчислити: а) 2. Обчислити: а) 3. Розкрити дужки і знайти значення виразу 4. Розв’язати рівняння 42 + (x – 7) = –13.
5. Спростити вираз 2 b – (–3 a + d) – (c + 2 b) – 3 a і знайти його значення, якщо d = 12,13, c = 1,8. 6. Довжина відрізка MN координатної прямої дорівнює 3. Знайти координату точки N, якщо M(–2). Знайти всі розв’язки задачі. 7. Знайти суму всіх цілих розв’язків нерівності –4 < x < 2.
1. Розкрити дужки і знайти значення виразу 2. Розв’язати рівняння 3. Записати за допомогою букв і довести властивість: щоб від числа відняти суму двох інших чисел, можна від зменшуваного відняти один із доданків і від цієї різниці відняти інший доданок. 4. Розв’язати рівняння 7 – | x | = –3.
5. Обчислити периметр квадрата ABCD, якщо A(–5; 0) і В(–3; 0). 6. Довести, що сума всіх цілих розв’язків нерівності | x | < 40 дорівнює 0. 7. Розв’язати рівняння | x – 2| = 18.
1. –8 + (–12) =... а) 20; б) –20; в) –4; г) 4. 2. –9 + 19 =... а) –10; б) –28; в) 28; г) 10. 3. 7 + (–17) =... а) –24; б) 24; в) –10; г) 10. 4. –6 + 6 =... а) 0; б) –6; в) 6; г) –12. 5. 2 – 15 =... а) 13; б) –13; в) –17; г) 17. 6. –13 – 6 =... а) –19; б) 19; в) –7; г) 7. 7. 18 – (–9) =... а) 11; б) –11; в) 27; г) –27. 8. –4 – (–3) =... а) –7; б) 7; в) –1; г) 1.
9. –8 + (–2) + 8 =... а) –18; б) 14; в) 2; г) –2. 10. –13 + (– y + x) =... а) –13 + y + x; б) –13 – y – x; в) –13 – y + x; г) –13 + y – x. 11. –10 – (–10 + y) =... а) –20 + y; б) –20 – y; в) y; г) – y. 12. Якщо точки А(–1) і В(13) є кінцями відрізка АВ, то довжина цього відрізка дорівнює значенню виразу: а) –1 – 13; б) 13 – (–1); в) –1 + 13; г) 13 + (–1).
1. Обчислити: а) –19 + (–54); б) –63 + 24; в) 81 + (–13). 2. Обчислити: а) 17 – 50; б) –33 – 16; в) 42 – (–19); г) –30 – (–5). 3. Розкрити дужки і спростити вираз: (b – 24,4) – (b – 43,6). 4. Розв’язати рівняння: а) 43 + x = 12; б) 25 – x = –9.
5. Обчислити відстань між точками А(–11) і В(17) координатної прямої. 6. Знайти значення виразу 23 – (–42) – 125.
1. Обчислити: а) 2. Обчислити: а) 3. Розкрити дужки і знайти значення виразу 4. Розв’язати рівняння 45 – (x – 60) = –2.
5. Спростити вираз 7 d – (–5 a – b) – (7 d + 5 a) + c і знайти його значення, якщо b = –10,42, c = 18,4. 6. Довжина відрізка PK координатної прямої дорівнює 6. Знайти координату точки K, якщо P(–4). Знайти всі розв’язки задачі. 7. Знайти суму всіх цілих розв’язків нерівності –3 < x < 1.
1. Розкрити дужки і знайти значення виразу 2. Розв’язати рівняння 3. Записати за допомогою букв і довести властивість: щоб від числа відняти різницю двох чисел, можна від нього відняти зменшуване і до результату додати від’ємник. 4. Розв’язати рівняння 4 – | x | = –4.
5. Обчислити периметр рівностороннього трикутника ABC, якщо 6. Довести, що сума всіх цілих розв’язків нерівності | x | < 23 дорівнює 0. 7. Розв’язати рівняння | x + 1| = 15.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 573; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.152 (0.009 с.) |

 ; б)
; б)  ; в)
; в) 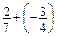 .
.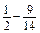 ; б)
; б) 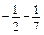 ; в)
; в)  .
. .
.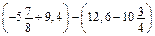 .
.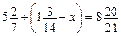 .
.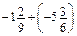 ; б)
; б)  ; в)
; в) 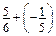 .
.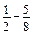 ; б)
; б)  ; в)
; в)  .
. .
.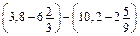 .
. .
.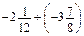 ; б)
; б)  ; в)
; в) 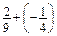 .
.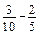 ; б)
; б) 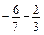 ; в)
; в) 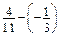 .
. .
. .
.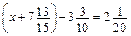 .
.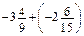 ; б)
; б) 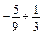 ; в)
; в)  .
.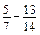 ; б)
; б) 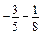 ; в)
; в) 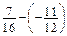 .
.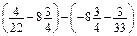 .
.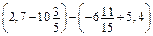 .
. .
. ; б)
; б)  ; в)
; в) 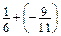 .
.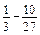 ; б)
; б) 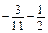 ; в)
; в) 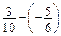 .
.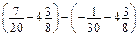 .
.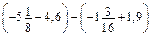 .
. .
. ; б)
; б) 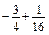 ; в)
; в) 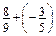 .
. ; б)
; б) 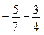 ; в)
; в) 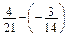 .
. .
.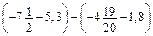 .
.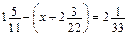 .
.


