Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чотирикутники. Площі. Призма. ПірамідаСодержание книги Поиск на нашем сайте
Тест 1. Чотирикутники
1. На яких рисунках прямі перпендикулярні? а); б); в); г); д); е). 2. На яких рисунках прямі паралельні? а); б); в); г); д); е).
Рисунок до задач 1–2 3. На яких рисунках зображено паралелограм? а); б); в); г); д); е). 4. На яких рисунках зображено трапецію? а); б); в); г); д); е).
Рисунок до задач 3–4
а) 36 см2; б) 18 см2; 6. Чому дорівнює площа трикутника ABD, зображеного на рисунку, якщо BM = 8 см і AD = 10 см? а) 40 см2; б) 20 см2; в) 80 см2; г) 26 см2. 7. Сторони трикутника, що утворюють прямий кут, дорівнюють 6 см і 8 см. Знайти площу цього трикутника. а) 14 см2; б) 12 см2; в) 48 см2; г) 24 см2.
а) 128 см2; б) 64 см2;
Тест 2
1. На якому з рисунків зображено чотирикутну призму? а); б); в); г). 2. На якому з рисунків зображено трикутну піраміду? а); б); в); г).
Рисунок до задач 1–2 За рисунком дати відповідь на запитання до задач 3–5.
а) три; б) дві; 4. Скільки бічних граней має призма? а) дві; б) три; 5. Площа однієї основи трикутної призми дорівнює a см2, а бічні грані рівні та площа кожної з них дорівнює b см2. Який з виразів відповідає обчисленню площі повної поверхні? а) (a + 3 b) см2; б) (2 a + 3 b) см2; в) (2 a + 4 b) см2; г) (2 a + 4 b) см2. За рисунком дати відповідь на запитання до задач 6–7.
а) одну; б) дві; 7. Скільки бічних граней має піраміда? а) одну; б) три;
3. Обчислити об’єм прямої призми, площа основи якої дорівнює 40 дм2, а висота — 15 дм. 4. Основою піраміди є трикутник, площа якого дорівнює 20 см2. Площа кожної бічної грані піраміди дорівнює 30 см2. Обчислити площу повної поверхні піраміди.
2. Основою прямої призми є прямокутний трикутник. Його сторони, що утворюють прямий кут, дорівнюють 5 см і 12 см. Обчислити об’єм призми, якщо її висота дорівнює 15 см. 3. Площа кожної бічної грані трикутної піраміди дорівнює 20 см2. Знайти площу основи піраміди, якщо вона в 4 рази менша від площі бічної поверхні піраміди.
1. За розгорткою чотирикутної піраміди, у якої основою є квадрат, а бічні грані рівні, знайти площу її повної поверхні. 2. За даною розгорткою прямої призми обчислити її об’єм.
3. Скільки: 1) граней; 2) ребер; 3) бічних ребер; 4) вершин у стокутної призми?
4. Сторони паралелограма дорівнюють 10 см і 8 см. Висота, що проведена до сторони завдовжки 8 см, дорівнює 6 см. Знайти висоту паралелограма, що проведена до сторони 10 см.
Тест 1
1. На яких рисунках прямі перпендикулярні? а); б); в); г); д); е). 2. На яких рисунках прямі паралельні? а); б); в); г); д); е).
Рисунок до задач 1–2 3. На яких рисунках зображено паралелограм? а); б); в); г); д); е). 4. На яких рисунках зображено трапецію? а); б); в); г); д); е).
Рисунок до задач 3–4
а) 72 см2; б) 154 см2; 6. Чому дорівнює площа трикутника MKP, зображеного на рисунку, якщо MP = 11 см і KL = 7 см? а) 77 см2; б) 38,5 см2; в) 154 см2; г) 72 см2. 7. Сторони трикутника, що утворюють прямий кут, дорівнюють 10 см і 12 см. Знайти площу цього трикутника. а) 120 см2; б) 60 см2; в) 30 см2; г) 240 см2.
а) 100 см2; б) 200 см2;
Тест 2
1. На якому з рисунків зображено шестикутну призму? а); б); в); г). 2. На якому з рисунків зображено трикутну піраміду? а); б); в); г).
Рисунок до задач 1–2 За рисунком дати відповідь на запитання до задач 3–4.
а) дві; б) чотири; 4. Скільки бічних граней має призма? а) дві; б) три;
За рисунком дати відповідь на запитання до задач 5–7.
а) три; б) чотири; 6. Скільки бічних граней має піраміда? а) дві; б) п’ять
7. Площа основи піраміди дорівнює a см2, а бічні грані рівні та площа кожної з них дорівнює b см2. Який з виразів відповідає обчисленню площі повної поверхні? а) (3 a + b) см2; б) (2 a + 3 b) см2; в) 3 ab см2; г) (a + 3 b) см2.
3. Обчислити площу бічної поверхні прямої призми, периметр основи якої дорівнює 20 см, а висота — 8 см. 4. Основою піраміди є чотирикутник, площа якого дорівнює 30 см2. Площа кожної бічної грані піраміди дорівнює 12 см2. Обчислити площу повної поверхні піраміди.
2. Основою прямої призми є трикутник, одна зі сторін якого дорівнює 8 см, а висота, що проведена до неї, — 3 см. Обчислити об’єм призми, якщо її висота дорівнює 10 см. 3. Площа кожної бічної грані чотирикутної піраміди дорівнює 30 см2. Знайти площу основи піраміди, якщо вона в 6 разів менша від площі бічної поверхні піраміди.
1. За розгорткою трикутної піраміди, у якої основою є рівносторонній трикутник, а бічні грані рівні, знайти площу її бічної поверхні. 2. За даною розгорткою прямої призми, основою якої є квадрат, обчислити її об’єм.
3. Скільки: 1) граней; 2) ребер; 3) бічних ребер; 4) вершин у п’ятдесятикутної призми?
4. Сторони паралелограма дорівнюють 12 см і 8 см. Висота, що проведена до сторони завдовжки 12 см, дорівнює 6 см. Знайти висоту паралелограма, що проведена до сторони завдовжки 8 см.
Тест 1
1. На яких рисунках прямі перпендикулярні? а); б); в); г); д); е). 2. На яких рисунках прямі паралельні? а); б); в); г); д); е).
Рисунок до задач 1–2 3. На яких рисунках зображено паралелограм? а); б); в); г); д); е). 4. На яких рисунках зображено трапецію? а); б); в); г); д); е).
Рисунок до задач 3–4
а) 96 см2; б) 48 см2;
6. Чому дорівнює площа трикутника MPL, зображеного на рисунку, якщо ML = 8 см і PO = 12 см? а) 192 см2; б) 48 см2; в) 96 см2; г) 40 см2. 7. Сторони трикутника, що утворюють прямий кут, дорівнюють 5 см і 12 см. Знайти площу цього трикутника. а) 60 см2; б) 30 см2; в) 120 см2; г) 240 см2.
а) 90 см2; б) 45 см2;
Тест 2
1. На якому з рисунків зображено чотирикутну призму? а); б); в); г). 2. На якому з рисунків зображено трикутну піраміду? а); б); в); г).
Рисунок до задач 1–2 За рисунком дати відповідь на запитання до задач 3–5.
а) дві; б) три; 4. Скільки бічних граней має призма? а) одну; б) три; 5. Площа однієї основи трикутної призми дорівнює m см2, а бічні грані рівні та площа кожної з них дорівнює n см2. Який з виразів відповідає обчисленню площі повної поверхні? а) (m + 3 n) см2; б) (3 m + 2 n) см2; в) (2 m + 3 n) см2; г) (m + n) см2. За рисунком дати відповідь на запитання до задач 6–7.
а) п’ять; б) чотири; 7. Скільки бічних граней має піраміда? а) одну; б) чотири;
3. Сторони основи прямої трикутної призми дорівнюють 5 см, 6 см і 10 см. Обчислити площу бічної поверхні призми, якщо її висота дорівнює 10 см. 4. Основою піраміди є шестикутник, площа якого дорівнює 10 см2. Площа кожної бічної грані піраміди дорівнює 8 см2. Обчислити площу повної поверхні піраміди.
1. Основи трапеції дорівнюють 6 см і 8 см, а її площа дорівнює 35 см2. Обчислити висоту трапеції. 2. Основою прямої призми є трапеція з основами 6 см і 8 см та висотою 5 см. Обчислити об’єм призми, якщо її висота дорівнює 10 см. 3. Площа кожної бічної грані шестикутної піраміди дорівнює 15 см2. Знайти площу основи піраміди, якщо вона в 10 разів менша від площі бічної поверхні піраміди.
1. За розгорткою чотирикутної піраміди, у якої основою є квадрат, а бічні грані рівні, знайти площу її повної поверхні. 2. За даною розгорткою прямої призми обчислити її об’єм.
3. Скільки: 1) граней; 2) ребер; 3) бічних ребер; 4) вершин у двадцятикутної призми?
4. Дві сторони, що утворюють прямий кут трикутника, дорівнюють 12 см і 16 см, а третя сторона — 20 см. Знайти висоту трикутника, що проведена до третьої сторони.
Тест 1
1. На яких рисунках прямі перпендикулярні? а); б); в); г); д); е). 2. На яких рисунках прямі паралельні? а); б); в); г); д); е).
Рисунок до задач 1–2 3. На яких рисунках зображено паралелограм? а); б); в); г); д); е). 4. На яких рисунках зображено трапецію? а); б); в); г); д); е).
Рисунок до задач 3–4
а) 70 см2; б) 150 см2;
6. Чому дорівнює площа трикутника ACD, зображеного на рисунку, якщо AD = 20 см і CP = 15 см? а) 35 см2; б) 150 см2; в) 70 см2; г) 300 см2. 7. Сторони трикутника, що утворюють прямий кут, дорівнюють 4 см і 10 см. Знайти площу цього трикутника. а) 160 см2; б) 80 см2; в) 20 см2; г) 40 см2.
а) 80 см2; б) 160 см2;
Тест 2
1. На якому з рисунків зображено шестикутну призму? а); б); в); г). 2. На якому з рисунків зображено чотирикутну піраміду? а); б); в); г).
Рисунок до задач 1–2 За рисунком дати відповідь на запитання до задач 3–4.
а) три; б) дві; 4. Скільки бічних граней має призма? а) дві; б) три;
За рисунком дати відповідь на запитання до задач 5–7.
а) три; б) п’ять; 6. Скільки бічних граней має піраміда? а) чотири; б) три; 7. Площа основи піраміди дорівнює a см2, а бічні грані рівні та площа кожної з них дорівнює m см2. Який з виразів відповідає обчисленню площі повної поверхні? а) (a + 4 m) см2; б) (2 a + 4 m) см2; в) (a + 3 m) см2; г) (3 a + m) см2.
3. Обчислити площу бічної поверхні прямої призми, основою якої є трикутник зі сторонами 6 см, 8 см і 10 см, а висота призми дорівнює 20 см. 4. Основою піраміди є п’ятикутник, площа якого дорівнює 20 см2. Площа кожної бічної грані піраміди дорівнює 30 см2. Обчислити площу повної поверхні піраміди.
2. Основою прямої призми є паралелограм, одна зі сторін якого дорівнює 10 см, а висота, що проведена до неї, — 8 см. Обчислити об’єм призми, якщо її висота дорівнює 12 см. 3. Площа кожної бічної грані п’ятикутної піраміди дорівнює 14 см2. Знайти площу основи піраміди, якщо вона в 7 разів менша від площі бічної поверхні піраміди.
1. За розгорткою трикутної піраміди, у якої основою є рівносторонній трикутник, а бічні грані рівні, знайти площу її бічної поверхні. 2. За даною розгорткою прямої трикутної призми обчислити її об’єм.
3. Скільки: 1) граней; 2) ребер; 3) бічних ребер; 4) вершин у десятикутної призми?
4. Дві сторони, що утворюють прямий кут трикутника, дорівнюють 6 см і 8 см, а третя сторона — 10 см. Знайти висоту трикутника, що проведена до третьої сторони.
Тест 1
1. На яких рисунках прямі перпендикулярні? а); б); в); г); д); е). 2. На яких рисунках прямі паралельні? а); б); в); г); д); е).
Рисунок до задач 1–2 3. На яких рисунках зображено паралелограм? а); б); в); г); д); е). 4. На яких рисунках зображено трапецію? а); б); в); г); д); е).
Рисунок до задач 3–4
а) 60 см2; б) 120 см2; 6. Чому дорівнює площа трикутника ABD, зображеного на рисунку, якщо AD = 12 см і BK = 10 см? а) 60 см2; б) 120 см2; в) 240 см2; г) 44 см2. 7. Сторони трикутника, що утворюють прямий кут, дорівнюють 20 см і 10 см. Знайти площу цього трикутника. а) 100 см2; б) 200 см2; в) 400 см2; г) 30 см2.
а) 200 см2; б) 25 см2;
Тест 2
1. На якому з рисунків зображено п’ятикутну призму? а); б); в); г). 2. На якому з рисунків зображено п’ятикутну піраміду? а); б); в); г).
Рисунок до задач 1–2 За рисунком дати відповідь на запитання до задач 3–5.
а) одну; б) дві; 4. Скільки бічних граней має призма? а) вісім; б) шість;
5. Площа однієї основи чотирикутної призми дорівнює a см2, а бічні грані рівні та площа кожної з них дорівнює b см2. Який з виразів відповідає обчисленню площі повної поверхні? а) (2 a + 4 b) см2; б) (6 a + 2 b) см2; в) (a + 6 b) см2; г) (2 a + 6 b) см2. За рисунком дати відповідь на запитання до задач 6–7.
а) шість; б) п’ять; 7. Скільки бічних граней має піраміда? а) шість; б) п’ять;
3. Основою прямої трикутної призми є рівносторонній трикутник зі стороною 8 см. Обчислити площу бічної поверхні призми, якщо її висота дорівнює 10 см. 4. Основою піраміди є п’ятикутник, площа основи якого дорівнює 12 см2. Площа кожної бічної грані піраміди дорівнює 10 см2. Обчислити площу повної поверхні піраміди.
2. Основою прямої призми є прямокутний трикутник. Його сторони, що утворюють прямий кут, дорівнюють 5 см і 12 см, а третя сторона дорівнює 13 см. Обчислити площу повної поверхні призми, якщо її висота дорівнює 10 см. 3. Площа кожної бічної грані трикутної піраміди дорівнює 10 см2. Знайти площу повної поверхні піраміди, якщо площа основи у 5 разів менша від площі бічної поверхні піраміди.
1. За розгорткою трикутної піраміди, у якої основою є рівносторонній трикутник, а бічні грані рівні, знайти площу її бічної поверхні. 2. За даною розгорткою прямої призми обчислити її об’єм.
3. Скільки: 1) граней; 2) ребер; 3) бічних ребер; 4) вершин у тридцятикутної призми?
Тест 1
1. На яких рисунках прямі перпендикулярні? а); б); в); г); д); е). 2. На яких рисунках прямі паралельні? а); б); в); г); д); е).
Рисунок до задач 1–2 3. На яких рисунках зображено паралелограм? а); б); в); г); д); е). 4. На яких рисунках зображено трапецію? а); б); в); г); д); е).
Рисунок до задач 3–4
а) 110 см2; б) 55 см2; 6. Чому дорівнює площа трикутника ACD, зображеного на рисунку, якщо AD = 11 см і CK = 10 см? а) 110 см2; б) 55 см2; в) 220 см2; г) 22,5 см2. 7. Сторони трикутника, що утворюють прямий кут, дорівнюють 4 см і 8 см. Знайти площу цього трикутника. а) 32 см2; б) 16 см2; в) 8 см2; г) 64 см2.
а) 30 см2; б) 50 см2;
Тест 2
1. На якому з рисунків зображено чотирикутну призму? а); б); в); г). 2. На якому з рисунків зображено трикутну піраміду? а); б); в); г).
Рисунок до задач 1–2 За рисунком дати відповідь на запитання до задач 3–4.
а) п’ять; б) сім; 4. Скільки бічних граней має призма? а) шість; б) дві;
За рисунком дати відповідь на запитання до задач 6–7.
а) дві; б) одну; 6. Скільки бічних граней має піраміда? а) чотири; б) одну;
7. Площа основи піраміди дорівнює a см2, а бічні грані рівні та площа кожної з них дорівнює b см2. Який з виразів відповідає обчисленню площі повної поверхні? а) (2 a + 5 b) см2; б) (a + 5 b) см2; в) (a + 4 b) см2; г) (5 a + b) см2.
|
5. Чому дорівнює площа паралелограма ABCD, зображеного на рисунку, якщо BM = 8 см і AD = 10 см?
8. Основи трапеції дорівнюють 10 см і 6 см, а висота — 8 см. Чому дорівнює площа трапеції?
3. Скільки основ має призма?
6. Скільки основ має піраміда?
1. Відтворити малюнок у зошиті та за допомогою косинця і лінійки провести через точку А пряму b, перпендикулярну до прямої a та пряму c, паралельну прямій а.
2. Обчислити площу трапеції ABCD, якщо AD = 12 см, ВС = 8 см і BK = 6 см.
5. Обчислити площу паралелограма ABCD, якщо AD = 15 см, СK = 8 см.
1. Обчислити довжину відрізка BK, якщо площа паралелограма ABCD дорівнює 36 см2, а сторона AD — 9 см.
4. Площа трикутника ABC, зображеного на рисунку, дорівнює 9 см2. Обчислити площу трикутника ABD, якщо AC = 6 см, CD = 7 см.
5. Чому дорівнює площа паралелограма MNKP, зображеного на рисунку, якщо MP = 11 см і KL = 7 см?
8. Основи трапеції дорівнюють 12 см і 8 см, а висота — 10 см. Чому дорівнює площа трапеції?
3. Скільки основ має призма?
5. Скільки основ має піраміда?
1. Відтворити малюнок у зошиті та за допомогою косинця і лінійки провести через точку А пряму n, перпендикулярну до прямої m та пряму k, паралельну прямій m.
2. Обчислити площу паралелограма MNKL, якщо ML = 12 см, PN = 8 см.
5. Обчислити площу трапеції ABCD, якщо AD = 20 см, ВС = 8 см і CM = 10 см.
1. Обчислити довжину відрізка BK, якщо площа трикутника ABC дорівнює 15 см2, а сторона AС — 6 см.
5. Чому дорівнює площа паралелограма MPKL, зображеного на рисунку, якщо ML = 8 см і KS = 12 см?
8. Основи трапеції дорівнюють 12 см і 6 см, а висота — 10 см. Чому дорівнює площа трапеції?
3. Скільки основ має призма?
6. Скільки основ має піраміда?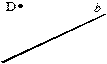
1. Відтворити малюнок у зошиті та за допомогою косинця і лінійки провести через точку D пряму c, перпендикулярну до прямої b та пряму a, паралельну прямій b.
2. Обчислити площу трапеції ABCD, якщо AD = 15 см, ВM = 8 см і BC = 12 см.
4. Обчислити площу паралелограма ABСK, якщо площа трапеції ABCD дорівнює 57 см2, а BC = 7 см, AD = 12 см.
5. Чому дорівнює площа паралелограма ABCD, зображеного на рисунку, якщо AD = 20 см і BK = 15 см?
8. Основи трапеції дорівнюють 6 см і 14 см, а висота — 8 см. Чому дорівнює площа трапеції?
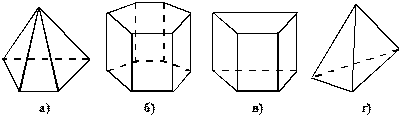
3. Скільки основ має призма?
5. Скільки основ має піраміда?
1. Відтворити малюнок у зошиті та за допомогою косинця і лінійки провести через точку D пряму c, перпендикулярну до прямої b та пряму m, паралельну прямій b.
2. Обчислити площу паралелограма MNKL, якщо NO = 7 см і NK = 10 см.
5. Обчислити площу трапеції ABCD, якщо AВ = 8 см, ВС = 6 см і AD = 12 см.
4. Обчислити площу трапеції ABCD, якщо площа паралелограма ABCM дорівнює 60 см2, а BC = 6 см, MD = 8 см.
5. Чому дорівнює площа паралелограма ABCD, зображеного на рисунку, якщо AD = 12 см і BK = 10 см?
8. Основи трапеції дорівнюють 14 см і 6 см, а висота — 5 см. Чому дорівнює площа трапеції?
3. Скільки основ має призма?
6. Скільки основ має піраміда?
1. Відтворити малюнок у зошиті та за допомогою косинця і лінійки провести через точку K пряму n, перпендикулярну до прямої m та пряму l, паралельну прямій m.
2. Обчислити площу трапеції MNKL, якщо NK = 6 см, ML = 8 см і KL = 4 см.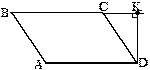
5. Обчислити площу паралелограма ABCD, якщо ВС = 12 см і KD = 7 см.
1. Обчислити довжину відрізка ВK, якщо площа трикутника ABC дорівнює 15 см2, а його сторона AВ — 6 см.
4. На малюнку СМ||АВ. Обчислити площу трапеції ABCD, якщо площа трикутника CMD дорівнює 80 см2, MD = 10 см, BC = 6 см.
4. Периметр паралелограма ABCD дорівнює 28 см. Знайти периметр паралелограма ABMK, якщо відрізок MC = 2 см.
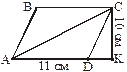5. Чому дорівнює площа паралелограма ABCD, зображеного на рисунку, якщо AD = 11 см і CK = 10 см?
8. Основи трапеції дорівнюють 13 см і 7 см, а висота — 10 см. Чому дорівнює площа трапеції?
3. Скільки основ має призма?
5. Скільки основ має піраміда?
