
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Три направления в истории моделированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Вопросы к экзамену
Три направления в истории моделирования
Моделирование является неотъемлемой стороной человеческой деятельности — от живописи до математического моделирования сложных систем и имеет многовековую историю. По существу, сама история науки и техники — это история развития моделирования явлений, процессов и объектов. Моделирование как познавательный прием неотделимо от развития знания. Поэтому понятия ≪ моделирование ≫ и ≪ модель ≫ играли жизненно важную роль в деятельности человечества с тех пор, как оно стало стремиться к пониманию и изменению окружающей среды. Моделирование как форма отражения действительности зародилась с возникновением научного знания. Модели и моделирование широко использовались в эпоху Возрождения; так, итальянские архитекторы того времени уже создавали модели проектируемых сооружений. Первоначально моделирование носило материальный и наглядный характер: модель представляла собой рисунок, макет, схему,чертеж и т. п. Возможность (и необходимость) представления знанийв виде моделей была понята не сразу, например, древние философы считали, что отобразить явления природы можно только с помощью словесных моделей (по современной терминологии — вербальных). В истории моделирования можно выделить три направления. Первое из них связано с технологией литья в формы, которые создавались по соответствующим образцам-моделям. Второе направление связано с материальными макетами объектов, которые Использовались при решении архитектурно-строительных и технических задач. Третье направление образовано научными знаниями, для осознания модельного характера которых потребовалось двадцать с лишним веков развития науки.
Основные понятия моделирования Объект моделирования и (оригинал) – некий объект реального мира, который может быть рассмотрен, как единое целое. Модель – объект произвольной природы, отражающий свойства, характеристики и связи моделируемого объекта, являющийся существенным для решения поставленных задач. Главное назначение модели состоит в упрощении получения информации о свойствах объекта-оригинала для решения конкретных практических задач. Полное соответствие модели оригиналу невозможно по определению, поскольку в этом случае теряются все преимущества моделей, так как мы фактически получим второй экземпляр объекта-оригинала с малодоступным для изучения бесконечным набором свойств. Самое распространенное представление о модели связано с материальной моделью, — например, с макетом. Однако моделями также являются экспериментальная установка, словесное описание объекта-оригинала, его мысленный образ и т. д. Понятие модели включает в себя следующие основные компоненты: объект-оригинал, решаемую задачу, характер отражаемых свойств объекта-оригинала, способ построения и способ реализации модели. При этом решаемая задача является одним из главных элементов, определяющим характер создаваемой модели. Именно решаемая задача определяет выбор существенных свойств моделируемого объекта, вид и способ построения модели. Без связи с конкретной задачей понятие модели не имеет смысла. Следующие факторы определяют множественность моделей, используемых для описания и исследования объекта. 1. Любой объект имеет бесконечное количество свойств; следовательно, для его разностороннего изучения необходимо построить множество моделей, каждая из которых будет отображать определенную группу его свойств. 2. Для одного и того же объекта, для отображения одних и тех же его свойств можно разными способами построить множество моделей в зависимости от целей моделирования и доступных средств. 3. Так как созданием моделей занимается конкретный человек (либо коллектив), построенная модель зачастую существенно зависит от его субъективных предпочтений. 4. В зависимости от решаемой задачи для одного и того же объекта одним и тем же способом, для отображения одних и тех же свойств можно построить множество моделей с разной степенью детализации описания свойств этого объекта. Назначение модели – упростить получение информации об оригинале для решения некоторых задач. Условно можно разделить модели на две группы: познавательные и прагматические. Познавательные модели являются формой представления знаний, поэтому при обнаружении расхождения между моделью и реальностью возникает задача устранения этого расхождения путем изменения модели. Познавательная деятельность ориентирована в основном на приближение модели к реальности, которую отображает модель. Познавательные модели широко используются в естественных науках; примером познавательной модели может служить модель солнечной системы. Прагматические модели являются средством организации практических действий, отображением цели. Примерами прагматических моделей могут служить проекты, рабочие чертежи и т. п. Прагматические модели носят нормативный характер, играют роль стандарта, образца, под который ≪подгоняются≫ как сама деятельность, так и ее результат: действительно, при создании нового объекта (например, строительстве здания) отклонение от проекта является недопустимым.
Факторы, определяющие множественность моделей. Понятие модели включает в себя следующие основные компоненты: объект-оригинал, решаемую задачу, характер отражаемых свойств объекта-оригинала, способ построения и способ реализации модели. При этом решаемая задача является одним из главных элементов, определяющим характер создаваемой модели. Именно решаемая задача определяет выбор существенных свойств моделируемого объекта, вид и способ построения модели. Без связи с конкретной задачей понятие модели не имеет смысла. Следующие факторы определяют множественность моделей, используемых для описания и исследования объекта. 1. Любой объект имеет бесконечное количество свойств; следовательно, для его разностороннего изучения необходимо построить множество моделей, каждая из которых будет отображать определенную группу его свойств. 2. Для одного и того же объекта, для отображения одних и тех же его свойств можно разными способами построить множество моделей в зависимости от целей моделирования и доступных средств. 3. Так как созданием моделей занимается конкретный человек (либо коллектив), построенная модель зачастую существенно зависит от его субъективных предпочтений. 4. В зависимости от решаемой задачи для одного и того же объекта одним и тем же способом, для отображения одних и тех же свойств можно построить множество моделей с разной степенью детализации описания свойств этого объекта. Таким образом, технология моделирования подразумевает вариативность в выборе типов моделей и получении ряда моделей, которые различаются степенью детализации описания объекта моделирования. Классификация по области использования модели Учебные модели – наглядные пособия, тренажеры, обучающие программы. Игровые модели – экономические, военные, деловые игры. Они репетируют поведение объекта в различных ситуациях. Исследовательские модели – создаются для исследования процессов или явлений, например, стенды для проверки электронной аппаратуры. Опытные модели – уменьшенные копии объектов. Имитационные модели – не просто отражают реальность, но имитируют ее. Эксперимент многократно повторяется. Классификация по отрасли представленных знаний Биологические Экологические Социальные Физические Актуальность моделирования. Издавна человек применяет модели. Это полезно при изучении сложных процессов или систем, конструировании новых устройств или сооружений. Обычно модель более доступна для исследования, чем реальный объект (а есть такие объекты, экспериментировать с которыми невозможно или недопустимо). Как вы уже знаете, модель -- это некоторый материальный или идеальный (мысленно представляемый) объект, замещающий объект-оригинал, сохраняя его характеристики, важные для данной задачи. Процесс построения модели называют моделированием. Все способы моделирования можно разделить на две большие группы. В одном случае моделью является предмет, воспроизводящий те или иные геометрические, физические и т.п. характеристики оригинала. Это -- материальное (физическое) моделирование. Исследование таких моделей -- реальные эксперименты с ними. По иному происходит работа с информационными (идеальными) моделями, являющимися описаниями объектов-оригиналов с помощью схем, графиков, формул, чертежей и т.п. Одним из важнейших видов информационного моделирования является математическое -- когда описания формулируются на языке математики. Соответственно, и исследование таких моделей ведется с использованием математических методов. Именно математическим моделированием вы пользуетесь при решении количественных задач на уроках физики и химии. Математические модели, используемые при решении современных практических задач, настолько сложны, что исследовать их вручную практически невозможно. Приходится прибегать к помощи компьютера. Как же происходит процесс компьютерного моделирования? Всякая модель создается для вполне определенной цели, и это в значительной степени определяет ее выбор. Поэтому первое, что необходимо сделать, -- поставить задачу, т.е. определить вопросы, ответы на которые мы хотим получить, и необходимые для этого исходные данные. Классификация моделей. Модель – объект произведенный природой, отражающий св-ва, харак-ки и связи моделируемого объекта, кот. явл. существенными для решения задач. Признаки классификации моделей: · по области использования; · по фактору времени; · по отрасли знаний; · по форме представления; · по признаку реализации и т. д. Классификация моделей по области использования: · Учебные модели – используются при обучении. · Опытные – это уменьшенные или увеличенные копии проектируемого объекта. Используют для исследования и прогнозирования его будущих характеристик. · Научно - технические - создаются для исследования процессов и явлений. · Игровые – репетиция поведения объекта в различных условиях. · Имитационные – отражение реальности в той или иной степени (это метод проб и ошибок). · Классификация моделей по фактору времени: · Статические – модели, описывающие состояние системы в определенный момент времени (единовременный срез информации по данному объекту). Примеры моделей: классификация животных…., строение молекул, список посаженных деревьев, отчет об обследовании состояния зубов в школе и тд. · Динамические – модели, описывающие процессы изменения и развития системы (изменения объекта во времени). Примеры: описание движения тел, развития организмов, процесс химических реакций. Классификация моделей по отрасли знаний (отрасли деятельности человека): · математические; · биологические; · химические; · социальные; · экономические; · исторические и т. д. Классификация моделей по форме представления: · Материальные – это предметные (физические) модели. Они всегда имеют реальное воплощение. Отражают внешнее свойство и внутреннее устройство исходных объектов, суть процессов и явлений объекта-оригинала. Это экспериментальный метод познания окружающей среды. Примеры: детские игрушки, скелет человека, чучело, макет солнечной системы, школьные пособия, физические и химические опыты. · Абстрактные (нематериальные) – не имеют реального воплощения. Их основу составляет информация. Это теоретический метод познания окружающей среды. · По признаку реализации: · Мысленные – формируются в воображении человека в результате раздумий, умозаключений, иногда в виде некоторого образа. Это модель сопутствует сознательной деятельности человека. · Вербальные – мысленные модели выраженные в разговорной форме. Используется для передачи мыслей. · Информационные – целенаправленно отобранная информация об объекте, которая отражает наиболее существенные для исследователя свойств этого объекта. Адекватность моделей.
Адекватность модели — совпадение свойств (функций/параметров/характеристик и т. п.) модели и соответствующих свойств моделируемого объекта. Адекватностью называется совпадение модели моделируемой системы в отношении цели моделирования. Проверку адекватности проводят на всех этапах построения модели, начиная с самого первого этапа - концептуального анализа. Если описание системы будет составлено не адекватно реальной системе, то и модель, как бы точно она не отображала описание системы, не будет адекватной оригиналу. можно говорить об адекватности модели в любой ее форме и оригинала, если: · описание поведения, созданное на каком-либо этапе, достаточно точно совпадает с поведением моделируемой системы в одинаковых ситуациях; · описание убедительно представительно относительно свойств системы, которые должны прогнозироваться с помощью модели. Предварительно исходный вариант математической модели подвергается следующим проверкам: · все ли существенные параметры включены в модель; · нет ли в модели несущественных параметров; · правильно ли отражены функциональные связи между параметрами; · правильно ли определены ограничения на значения параметров; · не дает ли модель абсурдные ответы, если ее параметры принимают предельные значения; Такая предварительная оценка адекватности модели позволяет выявить в ней наиболее грубые ошибки. Но все эти рекомендации носят неформальный, рекомендательный характер. Формальных методов оценки адекватности не существует! Поэтому, в основном, качество модели (и в первую очередь степень ее адекватности системе) зависит от опыта, интуиции, эрудиции разработчика модели и других субъективных факторов.
Требования, предъявляемые к моделям Универсальность - характеризует полноту отображения моделью изучаемых свойств реального объекта. Адекватность - способность отражать нужные свойства объекта с погрешностью не выше заданной. Точность модели различна в разных условиях функционирования объекта. Эти условия характеризуются внешними параметрами. В пространстве внешних параметров выделить область адекватности модели, где погрешность меньше заданной предельно допустимой погрешности. Точность - оценивается степенью совпадения значений характеристик реального объекта и значения этих характеристик полученных с помощью моделей. Экономичность - определяется затратами ресурсов ЭВМ памяти и времени на ее реализацию и эксплуатацию. ИЛИ (надо завтра уточнить) Пути решения мат. Модели: 1, Построение м. на основе законов природы (аналитич. Метод) 2. Формальный путь с помощью статистическ. Обработки и результатов измерения (статист. Подход) 3. Построение м. на основе модели элементов (сложных систем) Способ: 1, Аналитический – использование при достаточном изуч. Общей закономерности изв. Моделей. 2. эксперимент. При отсутствии информ. 3. Имитационная м. – исследует св-ва объекта сст. В целом. Пример построения математической модели. Математи́ческая моде́ль — это математическое представление реальности. Математическое моделирование — это процесс построения и изучения математических моделей. Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют объект его математической моделью и затем изучают последнюю. Связь математической модели с реальностью осуществляется с помощью цепочки гипотез, идеализаций и упрощений. С помощью математических методов описывается, как правило, идеальный объект, построенный на этапе содержательного моделирования. Зачем нужны модели? Очень часто при исследовании какого либо объекта возникают трудности. Сам оригинал порой бывает недоступен, или его использование не целесообразно, или привлечение оригинала требует больших затрат. Все эти проблемы можно решить с помощью моделирования. Модель в определенном смысле может заменить исследуемый объект. Простейшие примеры моделей § Фотографию можно назвать моделью человека. Для того чтобы узнать человека, достаточно видеть его фотографию. § Архитектор создал макет нового жилого района. Он может движением руки переместить высотное здание из одной части в другую. В реальности это было бы не возможно. Типы моделей Модели можно разделить на материальные' и идеальные. выше приведенные примеры являются материальными моделями. Идеальные модели часто имеют знаковую форму. Реальные понятия заменяются при этом некоторыми знаками, котое можно легко зафиксировать на бумаге, в памяти компьютера и т.д. Пример математической модели Задача Производственное объединение, в которое входят две мебельные фабрики, нуждается в обновлении парка станков. Причем первой мебельной фабрике нужно заменить три станка, а второй-семь. Заказы можно разместить на двух станкостроительных заводах. Первый завод может изготовить не более 6 станков, а второй завод примет заказ если их будет не мение трех. Требуется определить как размещать заказы. Решение Введем переменные: xij-количество станков, которое будет изготавливать i-й завод для j-й фабрики. По условию задачи: x11+x12 x21+x22 Кроме того, должны выполняться условия: x11+x21=3 x12+x22=7 Получаем систему ограничений в форме неравенств и уравнений: x11+x21=3 x12+x22=7 x11+x12 x21+x22 xij Мы составили математическую модель нашей задачи. Решая систему мы найдем множество различных решений. Вот одно из них: x 11 = 2, x 12 = 3, x 21 = 1, x 22 = 4. Оптимальное решение будет зависить от других параметров, отдаленности заводов, цены на станки и т.д. Таким образом, моделирование может значительно облегчить процесс изучения какого-либо объекта.
Оптимизационные модели. Экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия или критериев варианта использования имеющихся ресурсов (труда, капитала и пр.), называются оптимизационными. Оптимизационные задачи (ОЗ) решаются с помощью оптимизационных моделей (ОМ) методами математического программирования. Структура оптимизационной модели состоит из целевой функции, области допустимых решений и системы ограничений, определяющими эту область. Целевая функция в самом общем виде в свою очередь также состоит из трех элементов: - управляемых переменных; неуправляемых переменных; - формы функции (вида зависимости между ними). Область допустимых решений – это область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами, условиями, которые записываются в виде системы ограничений, состоящей из уравнений и неравенств. Оптимизационные задачи решаются методами математического программирования, которые подразделяются на: - линейное программирование; - нелинейное программирование; - динамическое программирование; - целочисленное программирование; - выпуклое программирование; исследование операций; - геометрическое программирование и др. Главная задача математического программирования – это нахождение экстремума функций при ограничениях в форме уравнений и неравенств.
Структурные модели. Четкого определения структурной модели не существует. Так, под структурной моделью устройства могут подразумевать: · структурную схему, которая представляет собой упрощенное графическое изображение устройства, дающее общее представление о форме, расположении и числе наиболее важных его частей и их взаимных связях; · топологическую модель, которая отражает взаимные связи между объектами, не зависящие от их геометрических свойств. Под структурной моделью процесса обычно подразумевают характеризующую его последовательность и состав стадий и этапов работы, совокупность процедур и привлекаемых технических средств, взаимодействие участников процесса. Например, — это могут быть упрощенное изображение звеньев механизма в виде стержней, плоских фигур (механика), прямоугольники с линиями со стрелками (теория автоматического управления, блок-схемы алгоритмов), план литературного произведения или законопроекта и т. д. Степень упрощения зависит от полноты исходных данных об исследуемом устройстве и потребной точности результатов. На практике виды структурных схем могут варьироваться от несложных небольших схем (минимальное число частей, простота форм их поверхностей) до близких к чертежу изображений (высокая степень подробности описания, сложность используемых форм поверхностей). Возможно изображение структурной схемы в масштабе. Такую модель относят к структурно-параметрической. Её примером служит кинематическая схема механизма, на которой размеры упрощенно изображенных звеньев (длины линий-стержней, радиусы колес-окружностей и т. д.) нанесены в масштабе, что позволяет дать численную оценку некоторым исследуемым характеристикам. Для повышения полноты восприятия на структурных схемах в символьном (буквенном, условными знаками) виде могут указывать параметры, характеризующие свойства отображаемых систем. Исследование таких схем позволяет установить соотношения (функциональные, геометрические и т. п.) между этими параметрами, то есть представить их взаимосвязь в виде равенств f (x1, х2, …) = 0, неравенств f (x1, х2, …) > 0 и в иных выражениях. Геоинформационные модели. Геоинформационно е моделирование базируется на создании многослойных элекронных карт, в которых опорный слой описывает географию определенной территории, а каждый из остальных — один из аспектов состояния этой территории. На географическую карту могут быть выведены различные слои объектов: города, дороги, аэропорты и др. Широкое распространение получили интерактивные географические карты (мира, различных частей света, России, Москвы и других городов) в Интернете. Такие карты обычно реализуются с использованием векторной графики и поэтому дают возможность пользователю выбирать нужный ему масштаб. Карты связаны с базами данных, которые хранят всю необходимую информацию об объектах, изображенных на картах. Например, на картографическом сервере можно сначала выбрать нужную карту из раскрывающегося списка, а затем выбрать вариант отображения карты (политико-административное деление, население, транспорт и так далее) — Если выбрать какой-либо регион на карте и щелкнуть на нем мышью, то появится окно с дополнительной информацией. Геоинформационные модели позволяют с помощью географических карт представлять статистическую информацию о различных регионах. Хранящаяся в базах данных информация о количестве населения, развитии промышленности, загрязнении огружающей среды и др. может быть связана с географическими картами и отображена на них. Отображение информации может производиться различными способами: закрашиванием регионов различными цветами, построением диаграмм и так далее. Можно построить в электронных таблицах Excel с использованием специальной надстройки Microsoft Data Map геоинформационную модель, отображающую информацию о количестве населения в различных странах мира.
Табличные модели. Представление информации в табличной форме широко распространено. Уже в школьной жизни приходится встречаться с массой таблиц: расписание занятий, журнал успеваемости, график дежурств, таблица Менделеева, таблицы физических свойств веществ, таблицы исторических дат и многое другое. Информация в таблицах обязательно упорядочена по какому-то принципу. Например, в классном журнале — в алфавитном порядке фамилий учеников; в расписании занятий — по дням недели и номерам уроков и т.д. Такая упорядоченность позволяет быстро находить в таблице нужные сведения. Чаще всего используются прямоугольные таблицы, состоящие из строк и столбцов (граф). В верхней строке таблицы обычно располагаются заголовки граф. Виды таблиц: · объект-свойство ( каждая строка такой таблицы относится к конкретному объекту ) · объект-объект ( отражают взаимосвязь между различными объектам) Информационные модели. Информационная модель — модельобъекта, представленная в виде информации, описывающей существенные для данного рассмотрения параметры и переменные величины объекта, связи между ними, входы и выходы объекта и позволяющая путём подачи на модель информации об изменениях входных величин моделировать возможные состояния объекта. Информационные модели нельзя потрогать или увидеть, они не имеют материального воплощения, потому что строятся только на информации. Информационная модель — совокупность информации, характеризующая существенные свойства и состояния объекта, процесса, явления, а также взаимосвязь с внешним миром. Информационные модели делятся на описательные и формальные. Описательные информационные модели - это модели, созданные на естественном языке (т.е. на любом языке общения между людьми: английском, русском, китайском, мальтийском и т.п.) в устной или письменной форме. Формальные информационные модели - это модели, созданные на формальном языке (т.е. научном, профессиональном или специализированном). Примеры формальных моделей: все виды формул, таблицы, графы, карты, схемы и т.д.
Транспортная задача. Транспортная задача - задача о поиске оптимального распределения поставок однородного товара от поставщиков к потребителям при известных затратах на перевозку (тарифах) между пунктами отправления и назначения. Является задачей линейного программирования специального вида. Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку). Решение транспортной задачи можно решить: · методом северо-западного угла Допустимое (но не всегда оптимальное с точки зрения стоимости доставки) начальное решение транспортной задачи можно построить, последовательно перебирая строки таблицы (то есть поставщиков) сверху вниз. В пределах каждой строки, нужно перебрать слева направо не охваченных или не полностью охваченных поставками потребителей, записывая в соответствующие ячейки объем поставляемого груза от поставщика в данной строке, и так до исчерпания возможностей поставщика. Таким образом, весь груз от поставщиков будет распределен по потребителям. Этот метод был предложен Данцигом в 1951 г. и назван Чарнесом и Купером «правилом северо-западного угла». · методом наименьшего элемента (минимальных тарифов) Записывать отгрузки в первую очередь в те ячейки, где тариф минимален. Этот метод позволяет получить более приближенное к оптимальному решение, которое, однако, может потребовать дальнейшей оптимизации. Метод минимальных тарифов с его модификациями (минимальный тариф по строке или минимальный тариф по столбцу) был описан Данцигом в работе 1951 г. · методом Фогеля · Метод потенциалов позволяет за несколько шагов (итераций) найти полностью оптимальное решение транспортной задачи. Перед решением задачи этим методом нужно найти допустимое начальное решение одним из методов, описанных в выше. Вопросы к экзамену
Три направления в истории моделирования
Моделирование является неотъемлемой стороной человеческой деятельности — от живописи до математического моделирования сложных систем и имеет многовековую историю. По существу, сама история науки и техники — это история развития моделирования явлений, процессов и объектов. Моделирование как познавательный прием неотделимо от развития знания. Поэтому понятия ≪ моделирование ≫ и ≪ модель ≫ играли жизненно важную роль в деятельности человечества с тех пор, как оно стало стремиться к пониманию и изменению окружающей среды. Моделирование как форма отражения действительности зародилась с возникновением научного знания. Модели и моделирование широко использовались в эпоху Возрождения; так, итальянские архитекторы того времени уже создавали модели проектируемых сооружений. Первоначально моделирование носило материальный и наглядный характер: модель представляла собой рисунок, макет, схему,чертеж и т. п. Возможность (и необходимость) представления знанийв виде моделей была понята не сразу, например, древние философы считали, что отобразить явления природы можно только с помощью словесных моделей (по современной терминологии — вербальных). В истории моделирования можно выделить три направления. Первое из них связано с технологией литья в формы, которые создавались по соответствующим образцам-моделям. Второе направление связано с материальными макетами объектов, которые Использовались при решении архитектурно-строительных и технических задач. Третье направление образовано научными знаниями, для осознания модельного характера которых потребовалось двадцать с лишним веков развития науки.
Основные понятия моделирования Объект моделирования и (оригинал) – некий объект реального мира, который может быть рассмотрен, как единое целое. Модель – объект произвольной природы, отражающий свойства, характеристики и связи моделируемого объекта, являющийся существенным для решения поставленных задач. Главное назначение модели состоит в упрощении получения информации о свойствах объекта-оригинала для решения конкретных практических задач. Полное соответствие модели оригиналу невозможно по определению, поскольку в этом случае теряются все преимущества моделей, так как мы фактически получим второй экземпляр объекта-оригинала с малодоступным для изучения бесконечным набором свойств. Самое распространенное представление о модели связано с материальной моделью, — например, с макетом. Однако моделями также являются экспериментальная установка, словесное описание объекта-оригинала, его мысленный образ и т. д. Понятие модели включает в себя следующие основные компоненты: объект-оригинал, решаемую задачу, характер отражаемых свойств объекта-оригинала, способ построения и способ реализации модели. При этом решаемая задача является одним из главных элементов, определяющим характер создаваемой модели. Именно решаемая задача определяет выбор существенных свойств моделируемого объекта, вид и способ построения модели. Без связи с конкретной задачей понятие модели не имеет смысла. Следующие факторы определяют множественность моделей, используемых для описания и исследования объекта. 1. Любой объект имеет бесконечное количество свойств; следовательно, для его разностороннего изучения необходимо построить множество моделей, каждая из которых будет отображать определенную группу его свойств. 2. Для одного и того же объекта, для отображения одних и тех же его свойств можно разными способами построить множество моделей в зависимости от целей моделирования и доступных средств. 3. Так как созданием моделей занимается конкретный человек (либо коллектив), построенная модель зачастую существенно зависит от его субъективных предпочтений. 4. В зависимости от решаемой задачи для одного и того же объекта одним и тем же способом, для отображения одних и тех же свойств можно построить множество моделей с разной степенью детализации описания свойств этого объекта. Назначение модели – упростить получение информации об оригинале для решения некоторых задач. Условно можно разделить модели на две группы: познавательные и прагматические. Познавательные модели являются формой представления знаний, поэтому при обнаружении расхождения между моделью и реальностью возникает задача устранения этого расхождения путем изменения модели. Познавательная деятельность ориентирована в основном на приближение модели к реальности, которую отображает модель. Познавательные модели широко используются в естественных науках; примером познавательной модели может служить модель солнечной системы. Прагматические модели являются средством организации практических действий, отображением цели. Примерами прагматических моделей могут служить проекты, рабочие чертежи и т. п. Прагматические модели носят нормативный характер, играют роль стандарта, образца, под который ≪подгоняются≫ как сама деятельность, так и ее результат: действительно, при создании нового объекта (например, строительстве здания) отклонение от проекта является недопустимым.
|
||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 2206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.013 с.) |

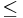 6
6 3
3


