Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклади розв’язання задач до теми 14Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача № 80 Інвестиційний проект інвестується 27 млрд.грн. Протягом трьох років поступає виручка однаковими сумами (по 20 млрд.грн.). Експерт по кредитам стверджує, що протягом наступних трьох років ставка проценту по кредитах не опуститься нижче 60%. Чи доцільний проект? Розв’язок задачі: Цю задачу можна розв’язувати двома шляхами: 1 спосіб: Якщо гроші інвестувати в проект, то через 3 роки отримаємо: в кінці 1 року: 20 млрд.грн. в кінці 2 року: 20 млрд.грн. + 20 млрд.грн. × 1,6 = 52 млрд.грн. в кінці 3 року: 20 млрд.грн. + 52 млрд.грн. × 1,6 = 103,2 млрд.грн. Якщо гроші вкласти гроші в банк, то через 3 роки отримаємо: SP = DV ×(1+r)t = 27 × (1 + 0, 6)3 = 27 × 1,63 = 110,6 млрд.грн. 103,2 млрд.грн. <110,6 млрд.грн. Відповідь: проект недоцільний. 2 спосіб: Для визначення доцільності проекту використовуємо формулу чистої дисконтованої вартості:
Підставляємо данні задачі у формулу:
Оскільки показник NDV має від’ємне значення, то цей проект є недоцільним. Задача 81 Фермер купляє ділянку землі 20 тис. грн. Він припускає, що чиста виручка протягом пяти років буде постійною, а потім він зможе продати ділянку за 25 тис грн. Ставка процента дорівнює 10%. Яка повинна бути мінімальна чиста щорічна виручка, щоб купівля землі виправдала себе. Розв’язок задачі: 1 спосіб розв’язання задачі: Якщо фермер покладе гроші в банк, то через 5 років він отримає: 20 × (1 + 0, 1)5 = 20 × 1,61 = 32,21 Позначимо мінімальну чисту щорічну виручку – х, тоді: після 1 року фермер отримає: х, який він покладе в банк; після 2 року фермер отримає: х + х ×1,1 = 2,1 х, який він покладе в банк; після 3 року фермер отримає: х + 2,1 х ×1,1 = 3,31 х, який він покладе в банк; після 4 року фермер отримає: х + 3,31 х ×1,1 = 4,641 х, який він покладе в банк; після 5 року фермер отримає: х + 4,641 х × 1,1 + 25 (від продажу землі) = 6,1051 х + 25, яка має бути не меншою ніж 32,21 тис.грн. 6,1051 х + 25 = 32,21 6,1051 х = 7,21 х = 1,18. 2 спосіб розв’язання задачі: Мінімальна чиста щорічна виручка має бути такою, щоб покрити інвестиції у землю, отже, чиста дисконтована вартість буде дорівнювати нулю. Позначимо мінімальну чисту щорічну виручку за «х» і підставимо данні задачі у формулу чистої дисконтованої вартості (
Приводимо до спільного знаменника: 20×(1+0,1)5 = х× (1+0,1)4 + х× (1+0,1)3 + х× (1+0,1)2 + х× (1+0,1)1 + х 32,2 = 1,46 х + 1,33 х + 1,21 х + 1,1 х + х + 25; 32,2 - 25 = 6,1 х; 7,2 = 6,1 х; х = 1,18 (тис. грн.)
Відповідь: мінімальна чиста щорічна виручка має бути не нижче 1,18 тис. грн.
Задача 82
Заключаючи контракт дві фірми вважають, що 20000 дол. сьогодні еквівалентні 34980 дол. через чотири роки. Визначить ставку відсотка на валютні вклади у банку. Вважаємо, що вона протягом чотирьох років не змінюється). Розв’язок задачі: Для розв’язання користуємося формулою: DV=SP/(1+r)t, де DV – дисконтована вартість, SP – ціна пропозиції (прейскурантна ціна капітального товару); t – період, за який ми хочемо одержати певний доход; r – норма відсотка. Підставляємо дані задачі: 20000 = 34980 / (1+r)4, (1+r)4 = 1,749 1+ r = 1,15 r = 0, 15 Відповідь: Ставка відсотка на валютні вклади у банку – 15 %. Задача 83 Передбачається, що верстат буде працювати 3 роки, і щорічно приносити 2000 грн. доходу. Його залишкова вартість в кінці 3-го року складе 6000 грн. Визначте поточну дисконтовану вартість верстата, якщо ставка відсотку складає 8%. Розв’язок задачі: Визначаємо сьогоднішню вартість майбутніх доходів від верстата. Для цього дисконтуємо доходи від верстату та залишкову вартість DV=SP/(1+r)t. 1 рік: сьогоднішня вартість 2000 грн. дорівнює: DV=2000/(1+0,08)1 = 1851,85 грн. 2 рік: сьогоднішня вартість 2000 грн. дорівнює: DV=2000/(1+0,08)2 = 1715, 27 грн. 3 рік: сьогоднішня вартість 2000 грн. доходу та залишкової вартості (6000 грн.) дорівнює: DV=(2000+6000)/(1+0,08)3 = 6349,21 грн. Складаємо сьогоднішні вартості всіх доходів:
1851,85 + 1715, 27 + 6349,21 = 9916,33 грн.
Задача 85 Місто потребує реконструкції мосту через річку, що розділяє його на дві частини. Дві фірми представили проекти реконструкції, що відрізняються за термінами виконання робіт та витратами:
Якому проекту слід віддати перевагу, якщо відсоткова ставка становить 10%? Розв’язок задачі: Розрахуємо поточну вартість витрат кожної фірми за формулою DV=SP/(1+r)t 1 фірма: 1 рік: DV = 2000/(1+0,1) = 1818,18 тис. грн. 2 рік: DV = 40000/(1+0,1)2 = 33057,85 тис. грн. 3 рік: DV = 0. Отже, поточна вартість всіх майбутніх витрат на реконструкцію складає: 1818,18 + 33057,85= 34876,03 тис. грн. 2 фірма: 1 рік: DV = 3000/(1+0,1) = 2727,27 тис. грн. 2 рік: DV = 15000/(1+0,1)2 = 12396,69 тис. грн. 3 рік: DV = 26000/(1+0,1)3 = 19548,87 тис. грн. Отже, поточна вартість всіх майбутніх витрат на реконструкцію складає: 2727,27 + 12396,69 + 19548,87 = 34672,76 тис. грн. Відповідь: оскільки у фірми 2 менші витрати (34876,03 > 34672,76), то слід віддати перевагу проекту реконструкції фірми 2. Задача 86 Фірма хоче взяти в оренду верстат, який коштує 20 тис. грн. і слугує 5 років. Визначте, якою повинна бути мінімальна річна орендна плата за експлуатацію верстата, якщо відсоткова ставка становить 10 %. Розв’язок задачі: Мінімальна річна рента має бути такою, щоб покрити інвестиції на верстат, отже, чиста дисконтована вартість буде дорівнювати нулю. Позначимо мінімальну річну ренту за «х» і підставимо данні задачі у формулу чистої дисконтованої вартості (
Приводимо до спільного знаменника: 20×(1+0,1)5 = х× (1+0,1)4 + х× (1+0,1)3 + х× (1+0,1)2 + х× (1+0,1)1 + х; 32,2 = 1,46 х + 1,33 х + 1,21 х + 1,1 х + х; 32,2 = 6,1 х; х = 5,28 (тис. грн.) Задача 87 Фірмі, що здійснює перевезення пасажирів по місту, пропонують купити ще одне маршрутне таксі за 350 тис. грн. Фірма очікує одержати від експлуатації маршрутного таксі доходи протягом трьох років: у перший рік – 200 тис. грн., на другий рік 100 тис. грн., на третій – 50 тис. грн. Наприкінці третього року фірма розраховує продати автомобіль за 60 тис. грн. Ставка відсотку – 10%. Визначте, чи буде вигідною для фірми така покупка. Розв’язок задачі: Доцільність покупки визначається показником чистої дисконтованої вартості за формулою: Підставляємо данні у формулу:
Оскільки показник від’ємний, фірмі невигідно купляти маршрутне таксі.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1194; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.231.160 (0.006 с.) |

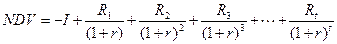
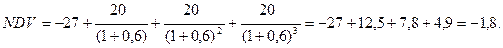
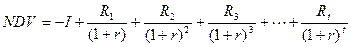 ):
):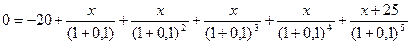
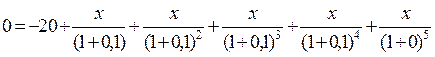 .
.