
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклади розв’язання задач до теми 8Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Приклади розв’язання задач до теми 8 Задача 54
У галузі функціонує 1000 фірм. Граничні витрати у кожної фірми за місяць становлять відповідно при рівні виробництва 5 одиниць товару – 2 гривні, 6 одиниць товару – 3 гривні, 7 одиниць – 5 гривень. Яким буде обсяг випуску продукції за місяць, коли ринкова ціна товару становитиме 3 гривні? Розв’язок задачі:
Для визначення обсягу випуску продукції користуємося правилом Р = МС. Оскільки при Q = 6 Р = МС = 3, то одна фірма буде виробляти 6 одиниць продукції. В галузі 1000 таких фірм, отже, галузь буде виробляти: 6×1000 = 6 000 одиниць продукції. Задача 55
Визначте двома способами (за сукупним та граничним підходом) оптимальний обсяг виробництва для фірми – досконалого конкурента, якщо ринкова ціна становить 130 грн., а сукупні витрати фірми наведені у таблиці. Який прибуток отримає фірма, обравши цей обсяг виробництва?
Розв’язок задачі:
Розв’язуємо задачу за сукупним підходом: Розраховуємо сукупний дохід та економічний прибуток і заносимо ці дані у таблицю:
Аналіз динаміки економічного прибутку показав, що максимізація прибутку буде в розмірі 260 тис. грн. при обсягах продукції 4 і 5 тис. шт. Розв’язуємо задачу за граничним підходом:
Оскільки всі одиниці продукції продаються по одній ціні, то Р= MR. Для визначення оптимального обсягу продукції, що максимізує економічний прибуток, користуємося золотим правилом мікроекономіки: МС= MR. З таблиці видно, що МС= MR=130 при Q = 5 тис. шт. Задача 57 Нижче представлена функція загальних витрат конкурентної фірми в короткостроковому періоді:
а) Який обсяг випуску продукції вибере фірма, якщо ринкова ціна товару складатиме: 3; 5; 7; 9 грн.? б) Який прибуток одержить фірма, якщо ринкова ціна товару складатиме: 3; 5; 7; 9 грн.? в) Якщо галузь складатиметься з 1000 фірм і кожна з них має таку ж функцію витрат, як наведено вище, то функція ринкової пропозиції буде виглядати таким чином:
г) Якщо функція ринкового попиту виглядатиме так, як наведено нижче, то яка буде рівноважна ціна продукту?
д) Яка величина обсягу випуску продукції кожної фірми? е) Який прибуток може одержати кожна фірма? є) Що буде робити фірма у довгостроковому періоді: входити в галузь чи виходити з неї?
Розв’язок задачі:
а) Для визначення обсягу випуску продукції користуємося правилом Р = МС. Тобто вибираємо обсяг продукції, за якого граничні витрати дорівнюють ціні або наближені до неї, але трохи нижчі за неї. при Р = 3 грн. → Q = 1 одиниць при Р = 5 грн. → Q = 2 одиниць при Р = 7 грн. → Q = 3 одиниць при Р = 9 грн. → Q = 4 одиниць
б) Прибуток розраховується як різниця між сукупним доходом та сукупними витратами π = TR – ТС TR = Р × Q → π = Р × Q – ТС при Р = 3 грн. → π = 3 × 1 – 12 = - 9 грн. при Р = 5 грн. → π = 5 × 2 – 16 = - 6 грн. при Р = 7 грн. → π = 7 × 3 – 22 = - 1 грн. при Р = 9 грн. → π = 9 × 4 - 30 = 6 грн. в) Якщо галузь складатиметься з 1000 фірм і кожна з них має таку ж функцію витрат, то функція ринкової пропозиції буде виглядати таким чином:
г) Тоді рівноважна ціна продукту – 5 грн. д) Величина обсягу випуску продукції кожної фірми – 2 одиниці. є) Кожна фірма може одержати збиток в розмірі – 6 грн. е) Оскільки фірми будуть отримувати збитки, то у довгостроковому періоді вони будуть виходити з галузі? Задача 58
Наведені в таблиці дані дають характеристику виробничої діяльності фірми. Який рівень випуску продукції буде відповідати максимізації прибутку фірми?
Розв’язок задачі: Розрахуємо прибуток при кожному обсязі випуску продукції. Для цього буде використана формула: π = TR – TC
Відповідь: Виходячи з даних таблиці фірма максимізує прибуток при обсягах продукції 22 і 23 одиниці. Задача 59 Ціна, витрати
MC ATC
MR
Q
На малюнку зображені криві витрат фірми, що діє в умовах конкурентної фірми. а) Покажіть на графіку рівень випуску, при якому прибуток фірми максимальний. б) Позначте на графіку площину, що представляє обсяг прибутку при даних рівнях ціни та випуску. в) Припустимо, що ця галузь знаходиться в рівновазі. Яка це буде рівновага: короткострокова чи довгострокова? г) Як може вплинути на дану фірму зменшення ринкового попиту на товари, що виробляються галуззю? Розв’язок задачі: а) Знаходимо обсяг продукції, користуючись правилом МR = МC, тобто перетин кривих МR і МC. На графіку рівень випуску Q1, при якому прибуток фірми максимальний. б) Для визначення прибутку знаходимо ціну та АТС для визначеного обсягу. На графіку затонована площина фігури представляє обсяг прибутку при даному рівні ціни та випуску. в) Ця галузь знаходиться в короткостроковій рівновазі, оскільки фірма отримує економічний прибуток, а у довгостроковому періоді фірма у стані рівноваги може отримувати тільки нормальний прибуток. г) Зменшення ринкового попиту на товари, що виробляються галуззю, може знизити економічний прибуток та обсяг випуску продукції даної фірми?
MC ATC
0 Q1 Q Задача 60 Розрахуйте дані середніх витрат для фірми для “Прайс-тейкера”.
а) Чи буде дана фірма виробляти у довгостроковому періоді по ціні 15 грн.? Чому? Якщо вона виробляє, яким буде обсяг виробництва, максимальний прибуток чи мінімальні збитки? Визначте величину прибутку чи збитку на одиницю продукції. б) Відповісти на питання а) при умові, що ціна дорівнює 20 грн. в) Теж саме при ціні 7 грн. г) Заповніть таблицю пропозиції фірми в короткостроковому періоді і визначте прибуток чи збиток отримані при кожному обсязі виробництва.
д) Що визначає криву пропозиції конкурентної фірми у короткостроковому періоді? Побудуйте графік, використовуючи дані задачі.
Розв’язок задачі: Заповнимо таблицю. Спочатку визначимо ТС. Відомо, що при Q=0 → ТС=ТFC. Відомо також що ТFC є постійною величиною при будь якому Q. Тому знаходимо ТFC при Q= 1 через формулу: AFC = ТFC/ Q → ТFC = АFC × Q = 30 × 1 =30. Тобто при Q=0 ТС=30. МС – це витрати на додаткову одиницю продукції. Отже, при Q=0 ТС=30, а на першу одиницю продукції треба ще додатково витратити 10, тоді для Q=1 ТС = 30 +10 =40. На виробництво другої одиниці продукції треба витрати 8, отже, Q=2 ТС = 40 + 8 = 48 і т.д. Після заповнення стовпчика ТС заповнюємо стовпчик АТС, користуючись формулою: АТС= ТС/ Q. Стовпчик AFC заповнюємо, користуючись формулою: AFC = ТFC/Q, враховуючи, що ТFC=30 і ця величина є незмінною для всіх Q. Стовпчик AVC заповнюємо, користуючись формулою: AVC= АТС-AFC.
а) Умова закриття фірми у довгостроковому періоді – Р < ATC. Обираючи можливий обсяг продукції користуємося правилом Р = МС. Якщо Р = 15 грн., то МС = 14, а можливий обсяг Q = 5. Перевіряємо АТС. При Q = 5 АТС = 15,2. Отже, 15 < 15, 2. Тоді фірма не буде виготовляти продукцію. б) Якщо Р = 20 грн., то МС = 14, а можливий обсяг Q = 5. Перевіряємо АТС. При Q = 5 АТС = 15,2. Отже, 20 > 15, 2. Тоді фірма буде виготовляти продукцію в обсязі 5 одиниць. Визначимо прибуток фірми за формулою: π = ТR – TC = P ∙ Q – TC. π = 20 ∙ 5 – 76 = 100 – 76 = 24 грн. Прибуток на одиницю продукції складе 24: 5 = 4,8 грн. в) Обираючи можливий обсяг продукції користуємося правилом Р = МС. Якщо Р = 7 грн., то МС менше за ціну не існує. Тоді фірма не буде виготовляти продукцію. г) Умова закриття фірми у короткостроковому періоді – Р ≤ AVC. Обираємо можливий обсяг продукції, користуючись правилом Р = МС. Заповнимо таблицю пропозиції фірми в короткостроковому періоді і визначимо прибуток чи збиток, отримані при кожному обсязі виробництва, за формулою π = ТR – TC = P × Q – TC.
д) Криву пропозиції конкурентної фірми у короткостроковому періоді визначає частина кривої граничних витрат, що знаходиться вище мінімуму кривої середніх змінних витрат, не включаючи точку мінімуму. Побудуємо графік, використовуючи дані задачі.
Задача 61 Використайте дану таблицю попиту для визначення валового та граничного доходу для кожного можливого обсягу продажу.
а) Що можна сказати про характер ринку, на якому ця фірма діє? Поясніть. б) Покажіть графічно криві попиту і граничного доходу для цієї фірми. Чому вони співпадають? Розв’язок задачі:

а) Оскільки всі одиниці продукції продаються за однаковою ціною, то фірма працює на ринку досконалої конкуренції. б) Оскільки всі одиниці продукції продаються за однаковою ціною, то криві попиту і граничного доходу фірми співпадають. Задача 62
На малюнку зображені криві витрат фірми, що працює в умовах досконалої конкуренції. а) В якому періоді зображена фірма? б) При якій ціні товару фірма повинна закрити виробництво? в) При якій ціні товару фірма отримувала б тільки нормальний прибуток? г) Чому дорівнюють загальні постійні витрати при ціні товару, яка забезпечує фірмі нормальний прибуток? д) В якому діапазоні цін фірма буде продовжувати виробництво зі збитками? е) Покажіть на графіку криву пропозиції для фірми? є) При яких цінах товару фірма могла б отримувати економічний прибуток у короткостроковому періоді? Розв’язок задачі: а) Оскільки існують постійні витрати, то фірма зображена у короткостроковому періоді. б) Фірма повинна закрити виробництво при ціні від 0 до В. в) Фірма отримувала б тільки нормальний прибуток при ціні 0D. г) Загальні постійні витрати при ціні товару, яка забезпечує фірмі нормальний прибуток, дорівнюють CDep. д) Фірма буде продовжувати виробництво зі збитками в діапазоні цін від В до D. е) Крива пропозиції для фірми зображена кривою МС вище точки k, не включаючи цю точку. є) Фірма могла б отримувати економічний прибуток у короткостроковому періоді при цінах вище D.
Задача № 63 Визначте двома способами (за сукупним та граничним підходом) оптимальний обсяг виробництва, ціну товару та прибуток для фірми-монополіста, якщо функція ринкового попиту на її товар Р=160-10 Q, а загальні витрати для кількох обсягів виробництва наведені у таблиці:
Розв’язок задачі: Визначимо оптимальний обсяг виробництва, ціну товару та прибуток за сукупним підходом. Ціну визначаємо підставляючи у формулу Р=160-10 × Q замість Q значення з таблиці: Р=160-10 × 0 = 160; Р=160-10 × 1 = 150; Р=160-10 × 2 = 140 і т.д.
З таблиці видно, що максимальний прибуток в розмірі 270 тис. грн. буде при обсязі 4 тис. од. та ціні 120 тис. грн./тис. од. (120 грн. за одиницю). Визначимо оптимальний обсяг виробництва, ціну товару та прибуток за граничним підходом розрахувавши граничний дохід (МR) та граничні витрати (МС), користуючись даними попередньої таблиці і формулами: МR = ∆ TR / ∆ Q; МС = ∆ TС / ∆ Q.
Для визначення оптимального обсягу виробництва користуємося золотим правилом мікроекономіки МR = МС. Оскільки такої рівності немає, то шукаємо обсяг продукції за якого ці показники найбільш наближені, але МR має бути більше МС. Отже, граничний підхід підтверджує оптимальний обсяг продукції 4 тис. од. Задача 65 Фірма цілком монополізувала виробництво. Наступна інформація відбиває положення фірми: MR = 1000 – 20Q; TR = 1000Q – 10 Q2; MC = 100 + 10Q. Скільки продукції і по якій ціні буде продано, якщо: а) фірма функціонує як проста монополія? б) фірма функціонує в умовах чистої конкуренції? Розв’язок задачі: а) Якщо фірма функціонує як проста монополія, то вона максимізує прибуток, коли: MR = MC. Підставляємо данні задачі: 1000 – 20Q = 100 + 10Q; 1000 – 100 = 30Q; 900 = 30Q; Q = 30 З формули TR = 1000Q – 10 Підставляємо Q = 30 у цю формулу Р = 1000 – 10 × 30 = 1000 – 300 = 700. б) Якщо фірма функціонує в умовах чистої конкуренції, то вона максимізує прибуток, коли: Р = MC З задачі відома функція MC = 100 + 10Q. З попереднього пункту відома функція ціни: Р = 1000 – 10 Q 1000 – 10 Q = 100 + 10Q; 1000 – 100 = 10Q + 10Q; 900 = 20 Q; Q = 45; Підставляємо Q = 45 у функцію ціни (Р = 1000 – 10 Q): Р = 1000 – 10 × 45 = 1000 – 450 = 550. Задача 66 Монополіст може продати 10 одиниць товару по ціні 100 грн. за одиницю, але продаж 11 одиниць викликає зниження ціни до 99,5 грн. Визначите граничний доход при збільшенні обсягу продажів з 10 до 11 одиниць. Розв’язок задачі: Граничний дохід - додатковий дохід, який є результатом продажу ще одної одиниці продукції:
При Q = 10 → TR = P × Q = 100 × 10 = 1000 $ При Q = 11 → TR = P × Q = 99,5 × 11 = 1094,5 $ Тоді MR = (1094,5 – 1000) / (11 – 10) = 94,5 $
Задача № 67
P
MC AТC MR D
Q На графіку висвітлено рівень доходу і витрат монопольної фірми. а) Визначте на графіку обсяг випуску продукції, що максимізує прибуток. б) Покажіть, за якою ціною монопольна фірма буде продавати продукцію в цьому випадку. в) Який прибуток він отримає? г) Пояснить, чому збільшення або зменшення визначеного обсягу випуску продукції буде скорочувати прибуток монопольної фірми?
Розв’язок задачі: а) Q1 ( знаходимона перетині кривих МС і МR, виходячи з золотого правила мікроекономіки: МС = МR ) - обсяг випуску продукції, що максимізує прибуток. б) P1 ( від Q1 піднімаємося до кривої попиту D ) - ціна монопольної фірми, за якою вона буде продавати продукцію в цьому випадку. в) визначаємо криву АТС (від Q1 піднімаємося до кривої АТС). Прибуток складе фігура – P1ACB. г) Якщо монополія буде виробляти менше продукції, ніж обсяг Q1, то вона недоотримає прибуток, тому що в цій ситуації граничні витрати нижчі за граничний дохід. Якщо монополія буде виробляти більше продукції, ніж обсяг Q1, то вона буде отримувати збиток з кожної додаткової одиниці продукції, тому що в цій ситуації граничні витрати вищі за граничний дохід.
MC
AТC MR D Q Задача 68
Малюнок зображує природну монополію. Галузь характеризується середніми витратами, що знижуються у довгостроковому періоді. а) Яку ціну та величину випуску вибере нерегульована монополія, що максимізує прибуток? б) Чому дорівнюють чисті втрати від монопольної влади, що виникають в результаті такого рішення? в) Який прибуток буде отримувати в такому випадку нерегульована монополія? г) Які параметри ціни та випуску визначають суспільно ефективний рівень виробництва? д) Якщо галузь націоналізована, а обсяг випуску і ціна відповідають суспільно ефективному рівню, то який розмір дотації необхідний такій галузі? е) При якій ціні та величині випуску економічний прибуток природної монополії дорівнює нулю? є) Які будуть чисті втрати суспільства, якщо держава встановить ціну для монополіста, що дорівнює середнім витратам? Розв’язок задачі:
а) Для відповіді на питання користуємося золотим правилом мікроекономіки: МС = МR. Отже, шукаємо точку перетину кривих МС і МR. Спускаємося на вісь Q. Тоді 0G - величина випуску продукції, яку вибере нерегульована монополія, що максимізує прибуток. Від G піднімаємося до кривої попиту (D) і виводимо на вертикальну вісь, щоб дізнатися ціну. Отже, 0К – ціна, яку вибере нерегульована монополія, що максимізує прибуток б) Якщо б галузь існувала в умовах чистої конкуренції, то виконувалася б умова: Р=МС. Отже, знаходимо перетин кривих граничних витрат (МС) та попиту (D) – це точка Y. Опускаємося від цієї точки на вісь Q. Тоді суспільству необхідно цього товару в розмірі 0S. Оскільки нерегульована монополія виробляє продукцію в обсязі 0G, то GS - збитки від монопольної влади, що виникають в результаті такого рішення. в) В п. а) були визначені обсяг виробництва та ціна нерегульованої монополії. Для визначення прибутку знаходимо собівартість (АТС). Для цього піднімаємося від G до кривої LAC і виводимо на вертикальну вісь. Отже, собівартість буде відрізок 0І. Тоді ІК – це прибуток на 1 одиницю продукції, а помноживши цей відрізок на обсяг продукції (0G), отримаємо KLWI – прибуток, який буде отримувати нерегульована монополія. г) В п. б) був визначений суспільно ефективний рівень виробництва 0S. Для визначення суспільно оптимальної ціни від S піднімаємося до кривої попиту(D) і виводимо на вертикальну вісь. Отже, 0A – ціна, що визначає суспільно ефективний рівень виробництва, д) Держава платить монополії дотації в розмірі збитків. Для визначення збитків, крім ціни, треба знати собівартість (ATC). Для цього від S піднімаємося до кривої LAC (точка N) і виводимо на вертикальну вісь. Отже, собівартість буде відрізок 0С. Тоді якщо ціна 0А, а собівартість 0С, то збиток на 1 одиницю продукції складе відрізок АС. Помноживши збиток на одинцю продукції на обсяг продукції (0S) виходить фігура CNYA - розмір дотації необхідний такій галузі. є) якщо економічний прибуток дорівнює нулю, то фірма отримує тільки нормальний прибуток, отже, ціна дорівнює собівартості (Р=АТС). Тоді шукаємо перетин кривих попиту і LAC (точка М) і виводимо на обидві осі. Отже, 0Е – ціна, коли економічний прибуток природної монополії дорівнює нулю; 0J - величина випуску, коли економічний прибуток природної монополії дорівнює нулю. е) Виходячи з попереднього пункту, якщо монополія буде виробляти 0J, а суспільству потрібно 0S (див. п. б)), то JS - чисті втрати суспільства, якщо держава встановить ціну для монополіста, що дорівнює середнім витратам.
Задача 69 Функція сукупних витрат монополіста: ТС = 100 + 3Q, де Q - кількість одиниць продукції, виробленої за місяць; функція попиту на продукцію монополіста: Р = 200 - Q, де Р - ціна продукції. Монополіст випускає 20 одиниць продукції за місяць. Який розмір його сукупного доходу? Якщо монополіст виробляє 19 одиниць продукції за місяць, як зміниться прибуток при підвищенні випуску продукції на одну одиницю? Розв’язок задачі: Якщо монополіст випускає 20 одиниць продукції за місяць, то розмір його сукупного доходу дорівнює:
TR = P × Q, Р = 200 – Q, → Р = 200 – 20 = 180, → TR = 180 × 20 = 3600.
Якщо монополіст виробляє 19 одиниць продукції за місяць, то при підвищенні випуску продукції на одну одиницю зміна прибутку буде визначатися наступним чином:
Δπ = π20 – π19 π = TR – ТС Шукаємо прибуток при 19 і при 20 одиницях продукції: при Q = 19 ТС = 100 + 3Q = 100 + 3 × 19 = 157, Р = 200 – Q, → Р = 200 – 19 = 181, → TR = 181 × 19 = 3439. π19 = TR – ТС = 3439 – 157 = 3282;
при Q = 20 ТС = 100 + 3Q = 100 + 3 × 20 = 160, Р = 200 – Q, → Р = 200 – 20 = 180, → TR = 180 × 20 = 3600. π20 = TR – ТС = 3600 – 160 = 3440;
Δπ = π20 – π19 = 3440 – 3282 = 158.
Відповідь: якщо монополіст виробляє 19 одиниць продукції за місяць, то при підвищенні випуску продукції на одну одиницю прибуток зміниться на 158. Задача 70 На ринку діють 6 фірм, кожна з яких має частку: 10%, 20%, 20%, 25%, 15%, 10%. Як зміниться індекс Герфіндаля, якщо об’єднаються друга та шоста фірми.
Розв’язок задачі: Користуємося формулою Герфіндаля: Визначаємо індекс Герфіндаля спочатку: Н = 102 + 202 + 202 + 252 + 152 + 102 = 100 + +400 + 400 + 625 + 225 + 100 = 1850. Якщо друга та шоста фірма об’єднаються, то друга фірма буде мати 20% + 10% = 30%. Тоді індекс Герфіндаля буде: Н = 102 + 302 + 202 + 252 + 152 = 100 + 900 + 400 + 625 + 225 = 2250.
Задача № 71 Припустимо, що на ринку оперують дві фірми (Х и Y), кожна з яких може виробляти “низький” або “ високий” обсяг продукції. Наведена нижче матриця демонструє можливі результати (прибуток) тих або інших рішень, що приймуть фірми. Над рискою показаний прибуток фірми Х, а під рисою - прибуток фірми Y при тій чи іншій стратегії. Припустимо, що Ви приймаєте рішення за фірму Х.
а) Якщо фірма Y вибирає “низький” обсяг випуску, то при якому рівні випуску Ваш прибуток максимальний? б) Якщо Ваша фірма Х вибере “високий” обсяг випуску, то при якому рівні випуску фірми Y її прибуток буде максимальний? в) Якщо фірма Y вибирає “високий” обсяг випуску, то при якому рівні випуску Ваш прибуток максимальний? г) У якому випадку Ви будете випускати “низький” обсяг продукції? д) Припустимо, Ви уклали угоду з Вашим конкурентом про те, що обидві фірми будуть випускати “низький” обсяг продукції. Які аргументи Ви наведете своєму конкуренту, щоб він не порушував угоди?
Розв’язок задачі: а) Якщо фірма Y вибирає “низький” обсяг випуску, то наш прибуток буде максимальним при високому рівні обсягу випуску. Якщо ми будемо випускати низький обсяг продукції, то будемо отримувати прибуток тільки 15 (верхній лівий прямокутник), а якщо будемо виробляти високий обсяг продукції, то будемо отримувати прибуток у розмірі 20(нижній лівий прямокутник). Оскільки 20 > 15, то ми будемо виробляти високий рівень продукції. б) Якщо Ваша фірма Х вибере “високий” обсяг випуску, то прибуток фірми Y буде максимальним при високому рівні обсягу випуску, оскільки 5 > 2. в) Якщо фірма Y вибирає “високий” обсяг випуску, то наш прибуток буде максимальним при високому рівні обсягу випуску, оскільки 8 > 2. г) Випуск може бути низьким тільки при укладенні угоди з конкурентом. д) Якщо ми уклали угоду з конкурентом про те, що обидві фірми будуть випускати “низький” обсяг продукції, то можна довести необхідність. не порушувати йому угоди таким чином: у випадку порушення з боку конкурента угоди, ми теж будемо випускати високий рівеннь продукції і тоді саме конкурент більше постраждає від порушення угоди, адже він отримає лише прибуток в розмірі 5, а ми – 8. Задача 72 Дослідження дуополістичного ринку встановило, що функції реагування кожної з двох фірм-виробників мають наступний вигляд: Y1 = 100 – 2 Y2; Y2 = 100 – 2 Y1, де Y1 та Y2 – обсяги виробництва відповідно першої та другої фірм. Зобразіть графічно функції реагування і обрахуйте пропорції розподілу ринку між ними.
Розв’язок задачі:
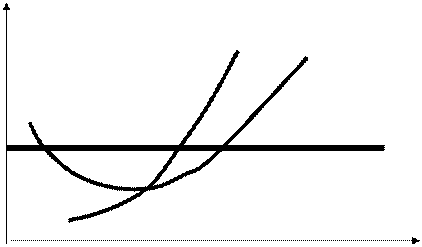
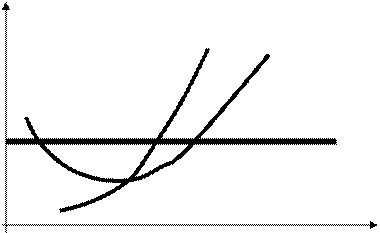
Будуємо графік реакції фірми 1 на випущену продукцію фірми 2. Підставляємо цифри у формулу Y1 = 100 – 2 Y2: якщо Y2 = 0, то Y1 = 100; якщо Y2 = 50, то Y1 = 0. Оскільки функція Y1 = 100 – 2 Y2 є лінійною, то цих двох координат достатньо для проведення прямої лінії. Аналогічно будуємо графік реакції фірми 2 на випущену продукцію фірми 1. Підставляємо цифри у формулу Y2 = 100 – 2 Y1: якщо Y1 = 0, то Y2 = 100; якщо Y1 = 50, то Y2 = 0. Оскільки функція Y2 = 100 – 2 Y1 є лінійною, то цих двох координат достатньо для проведення прямої лінії.
Y1 = 100 – 2 Y2 Y2 = 100 – 2 Y1 Розв’язуємо систему рівнянь: Y1 = 100 – 2 × (100 – 2 Y1) Y1 = 100 – 200 + 4 Y1 3 Y1 = 100 Y1 = 33,3 Тоді Y2 = 100 – 2 × 33,3 = 33,4 Відповідь: Обидві фірми виробляють продукцію в розмірі 33,3 кожна.Оскільки обидві фірми випускають однакову кількість продукції, то пропорції розподілу ринку між ними 50:50.
Задача 73 Крива ринкового попиту для дуополії Бертрана описується рівнянням: Р = 10 – Q. Граничні витрати фірм є сталим: МС = 2 грн. 1. Визначте рівноважні ціну і обсяг випуску для кожної фірми. 2. Визначте величину прибутку кожної фірми.
Розв’язок задачі: 1. При рівновазі Бертрана фірми встановлюють ціни як в умовах чистої конкуренції, тобто Р = МС, отже, ціна дорівнює 2 грн. Для визначення обсягу виробництва прирівнюємо Р = 10 – Q і МС = 2 грн. 10 – Q = 2 Q = 8. 2. Оскільки в умовах чистої конкуренції фірми отримують тільки нормальний прибуток, то економічний прибуток в умовах рівноваги Бертрана дорівнює нулю.
Задача № 74
AC
MR D 0 Q
На графіку показано фірму в умовах монополістичної конкуренції. а) В якому періоді зображена фірма? б) При якому обсязі випуску фірма максимізує прибуток чи мінімізує збитки? Якою буде ціна та величина прибутку (чи збитку)? в) Який обсяг продукції показує надлишкову виробничу потужність? г) Чи є ефективним ринок монополістичної конкуренції?
Розв’язок задачі: а) Фірма зображена у короткостроковому періоді, оскільки вона отримує економічний прибуток, а у довгостроковому періоді фірма у стані рівноваги може отримувати тільки нормальний прибуток. б) Фірма максимізує прибуток при обсязі випуску в) Оскільки суспільно оптимальний обсяг продукції буде, коли крива АС має точку мінімуму, то надлишкову виробничу потужність показує відрізок г) Ринок монополістичної конкуренції не є ефективним, оскільки в не виконуються умови ефективного розподілу ресурсів (Р = МС) та їх використання (Р = min ATC).
К В AC
MR D 0 Q
Задача 75 Функція сукупних витрат монополістичного конкурента має вигляд: ТС = 200 + 30 Q; функція попиту на продукцію фірми описується рівнянням: Р = 60 – 0,2 Q. 1. Визначте оптимальний обсяг випуску і ціну, які дозволять максимізувати прибуток фірми. 2. Визначте розмір прибутку фірми.
Розв’язок задачі: 1. Визначимо оптимальний обсяг продукції виходячи з золотого правила мікроекономіки: MR=МС. Граничні величини є похідними від сукупних величин, тобто: ТR' = MR; ТС' = MС МС = ТС' = ( 200 + 30 Q) ' = 30 ТR = Р ×Q = (60 – 0,2 Q) ×Q = 60 Q - 0,2 Q2 МR = ТR' = (60 Q - 0,2 Q2) ' = 60 – 0,4 Q Тепер використовуємо правило MR=МС: 60 – 0,4 Q = 30 0,4 Q = 30 Q = 75. Для визначення ціни підставляємо Q = 75 у функцію Р = 60 – 0,2 Q Р = 60 – 0,2 × 75 = 60 – 15 = 45. 2. Для визначення пр
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 5530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.01 с.) |

 P, C
P, C Р MR
Р MR
 АТС
АТС

 виводимо функцію ціни. Оскільки TR = Р × Q, то TR = Р × Q = Q (1000 – 10 Q) → Р = 1000 – 10 Q;
виводимо функцію ціни. Оскільки TR = Р × Q, то TR = Р × Q = Q (1000 – 10 Q) → Р = 1000 – 10 Q;


 P
P
 , де
, де  - частка ринку, що припадає на фірму, %; n – кількість фірм у галузі.
- частка ринку, що припадає на фірму, %; n – кількість фірм у галузі.


 Стратегія фірми X
Стратегія фірми X

 Розв’яжемо задачу математично:
Розв’яжемо задачу математично: P
P MC
MC

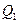


 P
P


